Một Vài Kĩ Thuật Giải Trắc Nghiệm

MỘT VÀI KĨ THUẬT GIẢI TRẮC NGHIỆM

Kĩ thuật 1. Sử dụng công thức tính nhanh, ghi nhớ công thức

Việc ghi nhớ một số công thức đặc biệt là quan trọng, giúp các bạn giải quyết bài toán rất nhanh. Tuy nhiên trong quá trình học, việc ghi nhớ phải thông qua chứng minh công thức để hiểu, không nên học vẹt.

Công thức 1. Cực trị của hàm bậc ba$y=a{{x}^{3}}+b{{x}^{2}}+cx+d$

Khi đó $y'=3a{{x}^{2}}+2bx+c$ và điều kiện để hàm số có cực đại cực tiểu là phương trình $y'=0$ có 2 nghiệm phân biệt $\Leftrightarrow \Delta '={{b}^{2}}-3ac>0$

Ví dụ 1 . Giá trị của m để hàm số $y=\frac{1}{3}{{x}^{3}}-\left( m-1 \right){{x}^{2}}+\left( m-3 \right)x-3$ có 1 cực đại và 1 cực tiểu là:

$[2;+\infty )$ B. $\left( -\infty ;1 \right]$

$\left( -\infty ;1 \right]\cup \left[ 2;+\infty \right)$ D. Đáp án khác

Giải.

Áp dụng : ${{b}^{2}}-3ac={{\left( -m+1 \right)}^{2}}-3.\frac{1}{3}.\left( m-3 \right)={{m}^{2}}-3m+2>0$

$\Leftrightarrow m>2\vee m<1$ $\Rightarrow $ Đáp án C đúng.

Công thức 2. Tứ diện vuông: là tứ diện có một góc tam diện ba mặt vuông.

Cho tứ diện O.ABC có các cạnh OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên mặt phẳng (ABC).

Khi đó ta có:

1) Hình chiếu H trùng với trực tâm tam giác ABC

2) $\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}$

3) ${{V}_{ABCD}}=\frac{1}{6}OA.OB.OC$

Chứng minh

Vì $OA\bot (OBC)$nên $BC\bot OA$

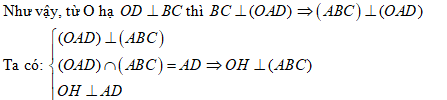
Vậy d(O; ABC) = OH.

Để tính OH, ta dựa vào hệ thức đường cao trong tam giác vuông AOD.

Ta có: $\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{D}^{2}}}$

Mặt khác: $\frac{1}{O{{D}^{2}}}=\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}$

Vậy: $\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}$

Ta khai thác hệ thức (2) kết hợp với tỉ lệ khoảng cách

Công thức 3. Tỉ lệ khoảng cách từ 2 điểm đến mặt phẳng $\left ( \alpha \right )$

Dựa vào tỉ lệ khoảng cách, ta có thể chuyển các điểm khó tính khoảng cách về điểm “gốc”

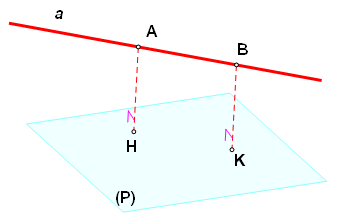
Nếu AB song song với mp $\left ( \alpha \right )$

Tính chất: nếu $AB//(\alpha )\Rightarrow d(A,(\alpha ))=d(B,(\alpha ))$

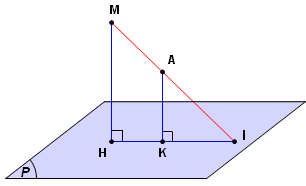
Nếu $MA\cap (\alpha )=I$

Dựng $MH\perp \left ( \alpha \right );AK\perp \left ( \alpha \right )\Rightarrow MH//AK\Rightarrow \frac{d(M,(\alpha ))}{d(A,(\alpha ))}=\frac{IM}{IA}$

Ví dụ 2 . Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2\[\sqrt{2}\]a, \[\widehat{ACB}={{45}^{0}}\]. Hình chiếu vuông góc H của đỉnh S trên mặt đáy là trung điểm cạnh AC và \[SH=a\]. Tính khoảng cách từ C đến mặt phẳng (SAB)

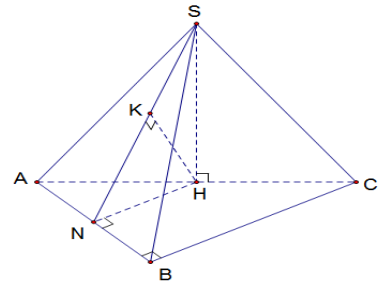
Ta có \[\frac{d(C;(SAB))}{d(H;(SAB))}=\frac{CA}{CH}=2\]\[\Rightarrow d(C;(SAB))=2d(H;(SAB))\]

Ta có \[HA\bot HB;HB\bot HC;HC\bot HA\]nên \[\frac{1}{{{d}^{2}}(H;(SAB)}=\frac{1}{H{{A}^{2}}}+\frac{1}{H{{B}^{2}}}+\frac{1}{H{{S}^{2}}}\]

Thay số ta tìm được khoảng cách từ C đến mp (SAB).

Công thức 4. Về nhân, chia môđun hai số phức.

Cho hai số phức \[{{z}_{1}};{{z}_{2}}\], ta có \[\left| {{z}_{1}}.{{z}_{2}} \right|=\left| {{z}_{1}} \right|.\left| {{z}_{2}} \right|\]

Ví dụ 3 . Cho số phức \[z=1+\sqrt{3}i\], tìm môđun của số phức \[\text{w}=(1-\sqrt{3}i){{z}^{2017}}\]

Ta có \[\left| \text{w} \right|=\left| (1-\sqrt{3}i){{z}^{2017}} \right|=\left| 1-\sqrt{3}i \right|\left| {{z}^{2017}} \right|=2.{{\left| z \right|}^{2017}}={{2.2}^{2017}}={{2}^{2018}}\]

Áp dụng. Cho số phức \[z=1-\sqrt{3}i\], tìm môđun của số phức \[\text{w}=(1+\sqrt{3}i){{z}^{2017}}.{{\overline{z}}^{2018}}\]

Kĩ thuật 2. Sử dụng máy tính cầm tay

1. Gán giá trị

Ví dụ 4 . Nếu $a={{\log }_{30}}3$ và $b={{\log }_{30}}5$ thì giá trị của ${{\log }_{30}}1350$là?

(A). ${{\log }_{30}}1350=2a+b+2$ (B). ${{\log }_{30}}1350=a+2b+1$

(C).${{\log }_{30}}1350=2a+b+1$ (D). ${{\log }_{30}}1350=a+2b+2$

Hướng dẫn : Gắn Shift STO A, B, gắn ${{\log }_{30}}1350=C$, sau đó xét hiệu C trừ đi các phương án, bằng 0 là đáp án đúng.

Ví dụ 5 . Cho ${{I}_{n}}=\int\limits_{0}^{1}{{{x}^{n}}{{e}^{-x}}dx},n\in {{\mathbb{N}}^{*}}$. Hệ thức nào sau đây đúng :

${{I}_{n+1}}=n{{I}_{n}}$
${{I}_{n+1}}=\left( n-1 \right){{I}_{n}}$
${{I}_{n+1}}=\left( n+1 \right){{I}_{n}}$
${{I}_{n+1}}=-\frac{1}{e}+\left( n+1 \right){{I}_{n}}$

Giải

Ta thấy nếu đáp án A, C, B đúng thì $\frac{{{I}_{n+1}}}{{{I}_{n}}}$ sẽ là số nguyên (vì n là số tự nhiên)

Vậy ta thử thay tại n = 1, bấm máy 3 lần tính ${{I}_{1}},{{I}_{2}},\frac{{{I}_{2}}}{{{I}_{1}}}$ và thấy $\frac{{{I}_{2}}}{{{I}_{1}}}$ không nguyên nên loại A, C, B.

Vậy đáp án đúng là D.

Ví dụ 6 . Cho tứ diện ABCD biết $A\left( 2;3;1 \right),B\left( 4;1;-2 \right),C\left( 6;3;7 \right),D\left( 1;-2;2 \right)$. Thể tích của tứ diện ABCD là

140(đvtt) B. 70(đvtt) C. $\frac{70}{3}$(đvtt) D. $\frac{70}{6}$(đvtt)

Giải.

Ta đã biết công thức sau : ${{V}_{ABCD}}=\frac{1}{6}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD} \right|$ (*)

Gán $\overrightarrow{AB}\left( 2;-2;-3 \right)$ cho VctA; Gán $\overrightarrow{AC}\left( 4;0;6 \right)$ cho VctB; Gán $\overrightarrow{AD}\left( -1;-5;1 \right)$ cho VctC

Cụ thể ta có các thao tác nhập như sau :

Kết quả ra là $\frac{70}{3}$ vậy ta chọn đáp án C.

Vận dụng

Giá trị nhỏ nhất của hàm số \[y={{e}^{x}}({{x}^{2}}-3)\] trên đoạn \[\left[ -2;2 \right]\] là:

\[\frac{6}{{{e}^{3}}}\] B. \[-2e\] C. \[{{e}^{2}}\] D. \[\frac{1}{{{e}^{2}}}\]

Tích hai nghiệm của phương trình \[{{2}^{2{{x}^{4}}+4{{\text{x}}^{2}}-6}}-{{2.2}^{{{x}^{4}}+2{{\text{x}}^{2}}-3}}+1=0\] là:

9 B. 1 C. -1 D. -9

Tìm m để hàm \[y=2{{x}^{3}}+3(m-1)+6(m-2)x+5\]có các điểm cực đại và cực tiểu và đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số song song với đường thẳng \[y=-25x-13\]

\[m=3\] B. \[m=4\] C. \[m=-2\] D. \[m=8\]

Tìm Giới hạn + Đạo hàm

Máy tính hỗ trợ trong việc tính đạo hàm tại một giá trị của x.

Ví dụ 7 . Đạo hàm của hàm số $y=\ln ({{x}^{2}}+x+1)$là?

(A). $\frac{2\text{x}+1}{\ln ({{x}^{2}}+x+1)}$ (B).$\frac{1}{({{x}^{2}}+x+1)}$ (C).$\frac{2\text{x}+1}{({{x}^{2}}+x+1)}$ (D).$\frac{1}{\ln ({{x}^{2}}+x+1)}$

Ta gán giá trị của x, ví dụ x = 2

Bấm máy tính \[{{\left. \frac{d}{dx}\left( \ln ({{x}^{2}}+x+1) \right) \right|}_{x=2}}\], kiểm tra ta thấy bằng ${{\left. \frac{2\text{x}+1}{({{x}^{2}}+x+1)} \right|}_{x=2}}$, chọn C.

Việc tìm giới hạn, chúng ta cần chọn giá trị của x phù hợp

Chú ý. Với hàm lượng giác, ta cần đổi đơn vị Radian.

Ví dụ 7 . Tính $M=\underset{n\to +\infty }{\mathop{\lim }}\,\left( {{n}^{2}}\ln \left( \text{cos}\frac{1}{n} \right) \right)$.

(A). 0 (B). $-\frac{1}{2}$ (C). $+\infty $ (D). Đáp án khác

Nhập hàm, sử dụng phím CALC, chọn $x={{10}^{9}}$ta có bảng sau. Chọn đáp án B.

Vận dụng

Tính $A=\underset{x\to 0}{\mathop{\lim }}\,\left[ \cot \text{x}\left( {{e}^{\sin 3\text{x}}}-1 \right) \right]$.

(A). 1 (B). 0 (C). 3 (D). $\frac{1}{3}$

Cho $A=\underset{x\to +\infty }{\mathop{\lim }}\,{{\left( \frac{x-2}{x+1} \right)}^{3\text{x}-4}}.$ Giá trị nào sau đây gần đúng với A nhất?

(A). -3 (B). 3 (C). 8 (D). -9

Giới hạn của $\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{{x}^{x}}$ là?

(A). e (B). $+\infty $ (C). 1 (D). 2

Giới hạn của $\underset{x\to +\infty }{\mathop{\lim }}\,{{\left( \frac{\text{cos}5\text{x}}{\text{cos3x}} \right)}^{\frac{1}{x\operatorname{s}\text{inx}}}}$ là?

(A). 1 (B). ${{e}^{-8}}$ (C). 0 (D). \[{{\text{e}}^{-4}}\]

Đạo hàm của hàm số $y={{e}^{{{\sin }^{2}}x}}$ là?

(A). ${{e}^{{{\sin }^{2}}x}}.c\text{os2x}$ (B). ${{e}^{{{\sin }^{2}}x}}.si{{n}^{2}}x$ (C). ${{e}^{{{\sin }^{2}}x}}.sin\text{2x}$ (D). ${{e}^{{{\sin }^{2}}x}}.c\text{o}{{\text{s}}^{2}}\text{x}$

Cho $f(x)=ln|sin2\text{x}|$ thì $f'(\frac{\pi }{8})$ bằng?

(A). 2 (B). 4 (C). 1 (D). 3

Kĩ thuật 3. Thử đáp án

Ví dụ 8 . Với giá trị nào của m thì hàm số $y={{x}^{3}}-3m{{x}^{2}}+3\left( {{m}^{2}}-1 \right)x-3{{m}^{2}}+5$ đạt cực đại tại $x=1$.

$m=1$ B. $m=2$ C. $m=0$ D. $m=0;\underset{{}}{\mathop{{}}}\,m=2$

Giải.

Thử 4 đáp án. Ở đây ta thấy đáp án C và D có chung $m=0$ trước, sau đó thử đến $m=2$ vì đáp án B và C có chung $m=2$. Nếu được rồi thì thôi còn không thì thử đáp án cuối cùng là A.

Nhập ${{\left. \frac{d\left( {{X}^{3}}-3M{{X}^{2}}+3\left( {{M}^{2}}-1 \right)X-3{{M}^{2}}+5 \right)}{dx} \right|}_{x=X}}:{{\left. \frac{d\left( 3{{X}^{2}}-6MX+3\left( {{M}^{2}}-1 \right) \right)}{dx} \right|}_{x=X}}$

$\xrightarrow[x=1;M=0]{CALC}0;6\Rightarrow $ Loại C; D.

Tiếp tục bấm CALC hoặc bấm tiếp dấu “=”.

Vận dụng

Tập nghiệm của bất phương trình ${{\left( 0,08 \right)}^{{{\log }_{0,5}}x}}\ge {{\left( \frac{5\sqrt{2}}{2} \right)}^{{{\log }_{0,5}}(2\text{x}-1)}}$ là:

(A) $[0;+\infty )$ (B) $(-\infty ;0]\cup (1;+\infty )$

(C) $\left( -\infty ;1 \right]$ (D)$\left ( -\infty ;\frac{1}{2} \right )\cup \left ( 1;+\infty \right )/\left \{ 0 \right \}$

Hàm số $y=f(x)={{x}^{3}}+a{{x}^{2}}+bx+c$ đạt cực tiểu tại $x=1;f(1)=-3$ và đồ thị cắt trục tung tại điểm có tung độ bằng 2 thì giá trị a, b, c là :

$a=2;b=-9;c=3$ B. $a=-3;b=-9;c=-2$

$a=3;b=-9;c=2$ D. $a=3;b=9;c=2$

Với giá trị nào của m thì hàm số $y=\sin 3x+m\sin x$ đạt cực đại tại điểm $x=\frac{\pi }{3}$

$m=5$ B. $m=-5$ C. $m=-6$ D. $m=6$

Kĩ thuật 4. Phương pháp loại trừ

Ví dụ 9 . Phương trình mặt phẳng (P) đối xứng với mặt phẳng (R) : $5x-2y+7z+2=0$ qua mặt phẳng Oxz là:

$-5x+2y-7z-2=0$
$5x-2y-7z-2=0$
$5x+2y+7z+2=0$
$-5x-2y-7z+2=0$

Giải.

Nhận thấy 1 điểm $M\left( x;y;z \right)$ bất kỳ khi lấy đối xứng qua mặt (Oxz) thì được điểm $M'\left( x;-y;z \right)$. Ta lấy điểm $M\left( 0;1;0 \right)\Rightarrow $ điểm đối xứng qua mặt (Oxz) là $M'\left( 0;-1;0 \right)$. Thay $M'\left( 0;-1;0 \right)$vào các đáp án thì chỉ có đáp án B và C thỏa mãn.

Tiếp tục ta lấy 1 điểm khác $N\left( 1;0;-1 \right)\Rightarrow $ điểm đối xứng là $N'\left( 1;0;-1 \right)$.

Thay $N'\left( 1;0;-1 \right)$vào các đáp án thì chỉ có đáp án C thỏa mãn.

Vậy đáp án C đúng.

Vận dụng

Đồ thị dưới đây là của hàm số nào?

\[y={{\log }_{3}}(x+1)\] B. \[y={{\log }_{2}}(x+1)\] C. \[y={{\log }_{3}}x\] D. \[y={{\log }_{2}}x+1\]

Hàm số nào sau đây có giá trị lớn nhất.

$y=2x+\sqrt{{{x}^{2}}+1}$ B. $y={{x}^{3}}-3x$

$y=-2{{x}^{4}}+{{x}^{2}}+1$ D. $y=\frac{1}{x}$

Kĩ thuật 5. Chọn tham số để đưa về dạng đặc biệt

Để nâng mức độ Vận dụng của bài toán, đề thường cho tham số để hạn chế thử phương án. Tuy nhiên, ta có thể gán tham số bằng các giá trị đặc biệt để tính.

Ví dụ 10 . Cho tứ diện đều ABCD cạnh a. Điểm M thuộc miền trong của khối tứ diện. Gọi ${{m}_{A}},{{m}_{B}},{{m}_{C}},{{m}_{D}}$ tương ứng là khoảng cách từ điểm M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Khi đó ${{m}_{A}}+{{m}_{B}}+{{m}_{C}}+{{m}_{D}}$bằng

$\frac{a\sqrt{3}}{3}$
$\frac{a\sqrt{6}}{3}$
$\frac{a\sqrt{3}}{2}$
$a\sqrt{3}$

Giải.

Chọn M là tâm mặt cầu ngoại tiếp của tứ diện và chọn $a=1$.

${{m}_{A}}={{m}_{B}}={{m}_{C}}={{m}_{D}}=\frac{1}{2\sqrt{6}}\Rightarrow {{m}_{A}}+{{m}_{B}}+{{m}_{C}}+{{m}_{D}}=\frac{4}{2\sqrt{6}}=\frac{\sqrt{6}}{3}$

Vậy chọn B.

Ví dụ 11 . Cho hàm số $y=-2{{x}^{3}}-3\left( 2a+1 \right){{x}^{2}}-6a\left( a+1 \right)x+2$ có cực trị tại ${{x}_{1}};{{x}_{2}}$ thì $\left| {{x}_{1}}-{{x}_{2}} \right|$ bằng

$\left| {{x}_{1}}-{{x}_{2}} \right|=a$
$\left| {{x}_{1}}-{{x}_{2}} \right|=1$
$\left| {{x}_{1}}-{{x}_{2}} \right|=2$
$\left| {{x}_{1}}-{{x}_{2}} \right|=a-1$

Giải.

Do đề bài sẽ đúng với mọi a nên ta cho a một giá trị đặc biệt để 4 đáp án là các giá trị khác nhau.

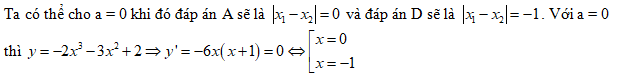
Nên $\left| {{x}_{1}}-{{x}_{2}} \right|=1$

Vậy ta chọn đáp án B.

Vận dụng

Đường thẳng $y=-x+m$ luôn cắt đồ thị $y=\frac{2x-1}{x+1}$ tại hai điểm P và Q. Để độ dài đoạn PQ ngắn nhất thì giá trị của m là :

$m=-1$ B. $m=1$ C. $m=-2$ D. $m=2$

Cho hàm số $f(x)={{x}^{3}}+\left( m-1 \right){{x}^{2}}-2\left( m+1 \right)x+m-2\underset{{}}{\mathop{{}}}\,\left( {{C}_{m}} \right)$ m là tham số. Điểm cố định mà đồ thị luôn đi qua là :

$M\left( 1;4 \right)$ B. $M\left( -1;-4 \right)$ C. $M\left( -1;4 \right)$ D. $M\left( 1;-4 \right)$

Kĩ thuật 6. Ứớc lượng

Ví dụ 12 . Cho hàm số $y=\frac{{{x}^{3}}+{{x}^{2}}-2x+1}{x+1}$. Số điểm trên đồ thị hàm số mà tọa độ của chúng đều thuộc ${{\mathbb{Z}}^{*}}$ là :

2 B. 3 C. 4 D. 0

Giải.

Cách thông thường : Với những hàm số phân thức có bậc của tử lớn hơn bậc của mẫu thì để tìm tọa độ nguyên ta cần thực hiện phép chia đa thức $y=\frac{{{x}^{3}}+{{x}^{2}}-2x+1}{x+1}={{x}^{2}}-2+\frac{3}{x+1}$

Khi đó để $y\in \mathbb{Z}\Leftrightarrow x+1\in $Ư (3)$=\left\{ -3;-1;1;3 \right\}$

Với $x+1=1\Rightarrow x=0\notin {{\mathbb{Z}}^{*}}\to $ loại

Với $x+1=3\Rightarrow x=2\Rightarrow y=3\to $ nhận

Với $x+1=-1\Rightarrow x=-2\Rightarrow y=-1\to $ nhận

Với $x+1=-3\Rightarrow x=-4\Rightarrow y=13\to $ nhận

Vậy có 3 điểm thỏa mãn. Chọn đáp án B.

Dùng ước lượng: Với cách này ta không cần phải chia đa thức cụ thể, chỉ cần biết khi chia đa thức thì y sẽ có dạng $y=....+\frac{a}{x+1}$ (mặt khác ${{x}^{3}}+{{x}^{2}}-2x+1=0$ không có nghiệm là $x=-1$ nên không chia hết cho hết $x+1$. Cứ mỗi số m là ước của a thì $-m$ cũng là ước của a nên số nghiệm x để thỏa mãn a chia hết cho (x + 1) là một số chẵn các số x. Để y nguyên thì (x + 1) ∈ Ư (a), do 1 luôn thuộc Ư (a) khi đó có $x+1=1\Rightarrow x=0$ (loại). Vậy số nghiệm nguyên x thỏa mãn đề bài là một số chẵn trừ đi 1 nên nó là số lẻ.

Chọn đáp án B.

Vận dụng