Tính Đơn Điệu Của Hàm Số

CHỦ ĐỀ 1 : TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

I. LÝ THUYẾT

1. Công thức đạo hàm

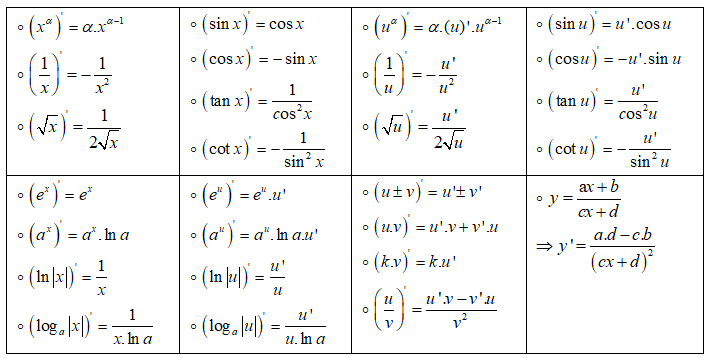
2. Tính đơn điệu của hàm số

a. Định nghĩa : Cho hàm số y = $f(x)$ xác định trên K

Hàm số y = $f(x)$ đồng biến trên K nếu $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})$
Hàm số y = $f(x)$ nghịch biến trên K nếu $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})>f({{x}_{2}})$

Chú ý : K là một khoảng hoặc đoạn hoặc nửa khoảng.

b. Định lý : Cho hàm số y = $f(x)$ xác định trên K

Nếu $f'(x)>0,\text{ }\forall x\in K$ thì hàm số $f(x)$ đồng biến trên K
Nếu $f'(x)<0,\text{ }\forall x\in K$ thì hàm số $f(x)$ nghịch biến trên K

c. Định lý mở rộng : Giả sử hàm số $y=f(x)$ có đạo hàm trên K

Nếu $f'(x)\ge 0,\text{ }\forall x\in K$ và $f'(x)=0$ chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K
Nếu $f'(x)\le 0,\text{ }\forall x\in K$ và $f'(x)=0$ chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên K
Nếu $f'(x)=0,\forall x\in K$ thì $f(x)$ không đổi trên K

II. VÍ DỤ MINH HỌA

Dạng 1 : Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số

Quy tắc :

Tìm tập xác định của hàm số
Tính đạo hàm $f'(x)$. Tìm các điểm ${{x}_{i}}(i=1,2,...,n)$ mà tại đó đạo hàm bằng 0 hoặc không xác định
Lập bảng biến thiên
Nêu kết luận về các khoảng đồng biến và nghịch biến của hàm số

Ví dụ 1 : Xét tính đồng biến, nghịch biến của hàm số sau :

a) $y={{x}^{3}}-6{{x}^{2}}+9x-4$ b) $y=\frac{x-2}{x+1}$

Lời giải :

a) TXĐ : $D=\mathbb{R}$

$y'=3x^2-12x+9\Rightarrow y'=0\Leftrightarrow x^2-4x+3=0\Leftrightarrow x=1$ hoặc $x=3$

Kết luận :

Hàm số đồng biến trên khoảng $\left( -\infty ;1 \right)$ và $(3;+\infty )$
Hàm số nghịch biến trên khoảng $\left( 1;3 \right)$.

b) TXĐ : $D=\mathbb{R}\backslash \left\{ -1 \right\}$

$y'=\frac{3}{{{\left( x+1 \right)}^{2}}}>0\forall x\ne -1$

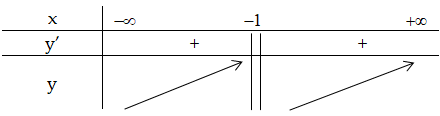
Kết luận : Hàm số đồng biến trên khoảng $\left( -\infty ;-1 \right)$ và $(-1;+\infty )$

BÀI TẬP ÁP DỤNG

Bài 1. Xét tính đồng biến , nghịch biến của hàm số :

a. $y=-\frac{1}{3}{{x}^{3}}+{{x}^{2}}-5x+3$ b. $y={{x}^{3}}-3{{x}^{2}}+3x+5$ c. $y={{x}^{3}}+{{x}^{2}}+2x-3$

d. $y=-{{x}^{3}}+3{{x}^{2}}+2$ e. $y=-\frac{1}{3}{{x}^{3}}+{{x}^{2}}-x+4$ f. $y=-{{x}^{3}}+2{{x}^{2}}-x+2$

g. $y={{x}^{3}}-{{x}^{2}}-5x+2$ h. $y=\frac{1}{3}{{x}^{3}}-{{x}^{2}}+x-5$

Bài 2. Xét tính đồng biến , nghịch biến của hàm số :

a. $y={{x}^{4}}-2{{x}^{2}}+5$ b. $y={{x}^{4}}+3{{x}^{2}}-4$ c. $y=-{{x}^{4}}+4{{x}^{2}}+3$

d. $y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}+1$ e. $y={{x}^{2}}-\frac{1}{4}{{x}^{4}}$ f. $y=-{{x}^{4}}-5{{x}^{2}}+1$

g. $y=-3{{x}^{4}}+4{{x}^{3}}+1$ h. $y={{\left( x+1 \right)}^{3}}\left( 5-x \right)$ i. $y={{\left( x+2 \right)}^{2}}{{\left( x-3 \right)}^{3}}$

Bài 3. Xét tính đồng biến , nghịch biến của hàm số :

a. $y=\frac{{{x}^{2}}+x+2}{x-1}$ b. $y=\frac{2x+1}{x-3}$ c. $y=1+\frac{3}{x+2}$ d. $y=\frac{3x+4}{1-x}$

e. $y=\frac{x+1}{{{x}^{2}}+8}$ f. $y=\frac{{{x}^{2}}-2x+2}{x-1}$ g. $y=\frac{{{x}^{2}}+x-5}{x+1}$

Dạng 2 : Tìm điều kiện của m để hàm số đồng biến, nghịch biến trên một khoảng K cho trước.

Phương pháp : Xét hàm số $y=f(x)$ trên K

Tính $f'(x)$
Nêu điều kiện của bài toán :

Hàm số đồng biến trên K $\Leftrightarrow f'(x)\ge 0,\forall x\in K$
Hàm số nghịch biến trên K $\Leftrightarrow f'(x)\le 0,\forall x\in K$

Từ điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất, tam thức bậc hai để tìm m

Ø CHÚ Ý : Cho hàm số $f(x)=a{{x}^{2}}+bx+c,(a\neq 0)$

$f(x)\geq 0,\forall x\in \mathbb{R}\Leftrightarrow \left\{\begin{matrix} a>0 & \\ \Delta \leq 0& \end{matrix}\right.$
$f(x)\leq 0,\forall x\in \mathbb{R}\Leftrightarrow \left\{\begin{matrix} a<0 & \\ \Delta \leq 0& \end{matrix}\right.$

Ví dụ 2 : Tìm m để hàm số : $y=\frac{1}{3}{{x}^{3}}+m{{x}^{2}}+4x-10$ đồng biến trên $\mathbb{R}$

Lời giải :

Ta có : $y'={{x}^{2}}+2mx+4$

Để hàm số đồng biến trên R thì ${{x}^{2}}+2mx+4\geq 0,\forall x\in \mathbb{R}\Leftrightarrow \left\{\begin{matrix} 1>0 & \\ \Delta '=m^2-4\leq 0& \end{matrix}\right.$

$\Leftrightarrow m\in \left[ -2;2 \right]$

Ví dụ 3 : Cho hàm số $y=-\frac{{{x}^{3}}}{3}+2{{x}^{2}}-mx+1$. Xác định m để :

Hàm số nghịch biến trên trên tập xác định của nó
Hàm số nghịch biến với mọi $x>1$

Lời giải :

a) Ta có : $y'=-{{x}^{2}}+4x-m$

Để hàm số nghịch biến trên R thì ${-{x}^{2}}+4x-m\leq 0,\forall x\in \mathbb{R}\Leftrightarrow \left\{\begin{matrix} -1<0 & \\ \Delta '=4-m^2\leq 0& \end{matrix}\right.$

$\Leftrightarrow m\geq 2\vee m\leq -2$

b) $y'=-{{x}^{2}}+4x-m,\Delta '=4-{{m}^{2}}$

Nếu $\Delta '\leq 0\Leftrightarrow m\geq 2\vee m\leq -2$ thì hàm số luôn nghịch biến trên R

Kết luận : Với $m\geq 2\vee m\leq -2$ thì hàm số nghịch biến với mọi $x>1.$

BÀI TẬP ÁP DỤNG

Bài 1. Cho hàm số $y=\frac{{{x}^{3}}}{3}-2m{{x}^{2}}+4mx+2$. Xác định m để :

Hàm số đồng biến trên miền xác định
Hàm số đồng biến trên khoảng $\left( -\infty ;0 \right)$

Bài 2. Tìm m để hàm số $y=\frac{1-m}{3}{{x}^{3}}-2(2-m){{x}^{2}}+2(2-m)x+5$ nghịch biến trên $\mathbb{R}$

Bài 3. Cho hàm số $f(x)=\frac{\cot x-1}{m\cot x-1},$ với $m$ là tham số. Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số nghịch biến trên khoảng $\left( 0;\frac{\pi }{3} \right).$

Chúc các bạn học tốt, thân!