A. LÝ THUYẾT
1. Độ lệch pha giữa hai dao động : Cho hai dao động điều hòa cùng phương cùng tần
số có phương trình dao động lần lượt : ${{x}_{1}}={{A}_{1}}c\text{os}\left(
\omega t+{{\varphi }_{1}} \right);{{x}_{2}}={{A}_{2}}c\text{os}\left( \omega
t+{{\varphi }_{2}} \right)$
Độ lệch pha giữa hai dao động :
$\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}$
Nếu $\Delta \varphi $ > 0 dao động 2 nhanh pha hơn dao động 1
Nếu
$\Delta \varphi $ < 0 dao động 2 trễ pha hơn dao động 1
Nếu $\Delta \varphi $ = 0 dao động 2
cùng pha với dao động 1
Nếu $\Delta \varphi =\pm \frac{\pi }{2}$ dao động 2 vuông pha với dao động 1.
2. Phương pháp giản đồ Fresnen (Phương pháp giản đồ vec tơ quay):
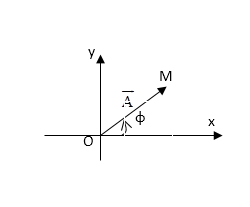 Lấy trục Ox theo phương ngang làm
chuẩn.
Lấy trục Ox theo phương ngang làm
chuẩn.
Vẽ vec tơ $\overrightarrow{OM}$có :
- Điểm đặt : tại O
Vec tơ $\overrightarrow{OM}$ hợp với trục Ox một góc φ
- Độ lớn : OM = A
Lưu ý :
φ > 0 vẽ $\overrightarrow{OM}$
trên trục Ox, φ < 0 vẽ $\overrightarrow{OM}$
dưới trục Ox, φ = 0 vẽ $\overrightarrow{OM}$ trùng với trục Ox.
3. Tổng hợp hai dao
động điều hòa cùng phương cùng tần số : Cho hai dao động điều hòa cùng
phương cùng tần số có phương trình dao động lần lượt : ${{x}_{1}}={{A}_{1}}c\text{os}\left(
\omega t+{{\varphi }_{1}} \right);{{x}_{2}}={{A}_{2}}c\text{os}\left( \omega
t+{{\varphi }_{2}} \right)$.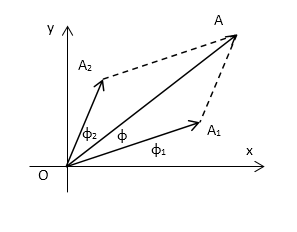
Tìm phương trình
dao động tổng hợp.
Biên độ dao động tổng
hợp
\[{{A}^{2}}={{A}_{1}}^{2}+{{A}_{2}}^{2}+2{{A}_{1}}{{A}_{2}}\cos
\left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)\]
Pha ban đầu của dao đông tổng hợp
\[\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}\]
Phương pháp 1: Phương pháp hình học
Tính $\Delta \varphi
={{\varphi }_{2}}-{{\varphi }_{1}}$
a.
Nếu $\Delta \varphi =0$ thì: A
= A1 + A2 $\varphi ={{\varphi }_{1}}={{\varphi }_{2}}$
b. Nếu $\Delta \varphi
=\pm \pi $ thì: $A=\left|
{{A}_{1}}-{{A}_{2}} \right|$; $\varphi ={{\varphi }_{1}}$ nếu A1
> A2; $\varphi ={{\varphi }_{2}}$ nếu A1 < A2
c. $\Delta
\varphi =\pm \frac{\pi }{2}$: $A=\sqrt{A_{1}^{2}+A_{2}^{2}}$
d.
A1 = A2: $A=2{{A}_{1}}\cos \frac{\Delta \varphi }{2}$
Phương
pháp 2: Phương pháp hình chiếu
$\overrightarrow{A}={{\overrightarrow{A}}_{1}}+{{\overrightarrow{A}}_{2}}$
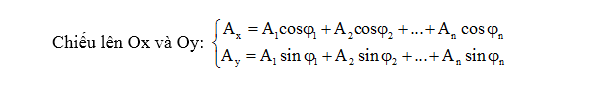
Khi đó: $A=\sqrt{A_{x}^{2}+A_{y}^{2}};\tan
\varphi =\frac{{{A}_{y}}}{{{A}_{x}}}$
Vẽ giản đồ vectơ dựa
trên giản đồ xác định giá trị của φ
Chú ý: Với bài toán từ 3 dao động thành phần trở lên ta dùng phương pháp 2 rất tiện lợi và hiệu quả.
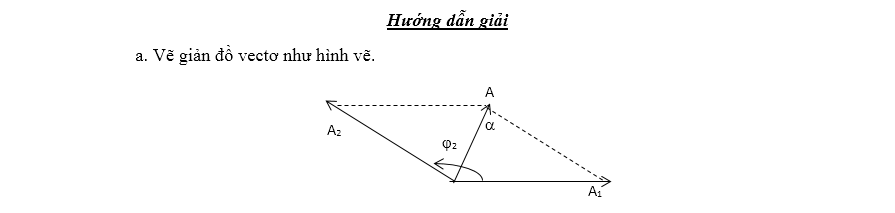
B. BÀI TOÁN TỔNG HỢP DAO ĐỘNG ĐIỀU HÒA DẠNG BIỆN LUẬN MAX
- MIN

a.
Tính giá trị của A1 .
b.
Viết phương trình dao động tổng hợp
c. Tính vận tốc của chất điểm tại thời điểm t = 0, suy ra tính chất của chuyển động khi đó.
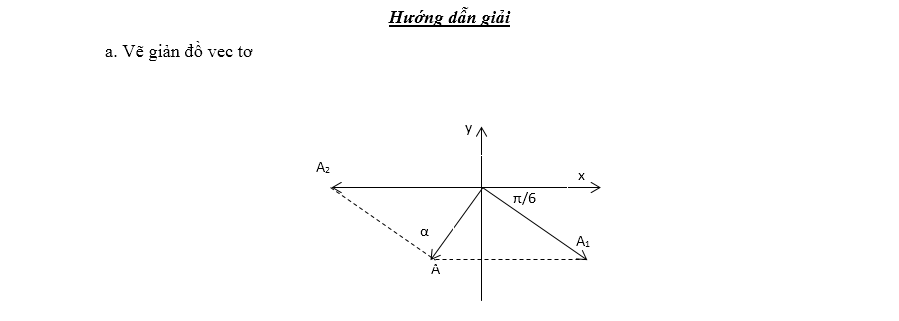
Dựa vào giản đồ vec tơ. Áp đụng định lý hàm số sin
$\frac{{{A}_{2}}}{\sin \alpha }=\frac{A}{\sin
\frac{\pi }{6}}\Rightarrow {{A}_{2}}=\frac{\text{A}\sin \alpha }{\sin \frac{\pi
}{6}}$ (1)
Từ (1) $\Rightarrow
{{A}_{2m\text{ax}}}$khi α = 900:
${{A}_{2}}=\frac{A}{\frac{1}{2}}=2A=18cm$
Tam giác OAA2
vuông tại A nên ta có:
$A_{1}^{2}+{{9}^{2}}=A_{2}^{2}\Rightarrow
{{A}_{1}}=\sqrt{A_{2}^{2}-{{9}^{2}}}=9\sqrt{3}cm$
b.
Dựa vào giản đồ vec tơ: $\varphi =\frac{\pi }{2}+\frac{\pi }{6}=\frac{2\pi
}{3}$
Vậy
phương trình dao động tổng hợp là: $x=9\cos \left( 4\pi t-\frac{2\pi }{3}
\right)cm$
c.
Ta có $v={{x}^{,}}=-36\pi \sin \left( 4\pi t-\frac{2\pi }{3}
\right)cm/s;a=-144{{\pi }^{2}}c\text{os}\left( 4\pi t-\frac{2\pi }{3}
\right)cm/{{s}^{2}}$
khi t = 0: $v=18\sqrt{3}\pi cm/s;a=72{{\pi }^{2}}cm/{{s}^{2}}\Rightarrow a.v>0$chất điểm chuyển động nhanh dần.
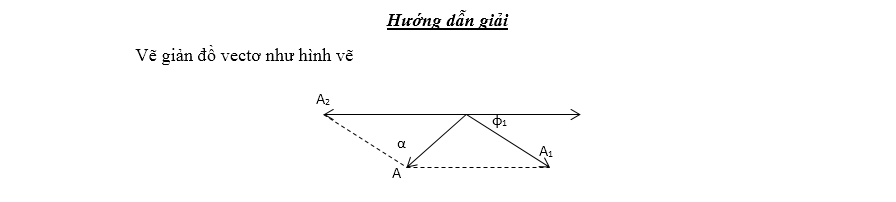
Bài 2: Một chất điểm thực hiện đồng
thời 2 dao đông điều hoà cùng phương: ${{x}_{1}}={{A}_{1}}c\text{os}\left(
10\pi t+\frac{\pi }{3} \right)cm$ ,${{x}_{2}}={{A}_{2}}c\text{os}\left( 10\pi
t-\frac{\pi }{2} \right)cm$. Phương trình dao động tổng hợp là 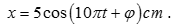 Biết biên độ
dao động A2 có giá trị lớn nhất
Biết biên độ
dao động A2 có giá trị lớn nhất
a. Tính A2max.
b. Viết phương trình dao động tổng
hợp.
c. Tính vận tốc của vật năng tại
ly độ x = 2,5cm.
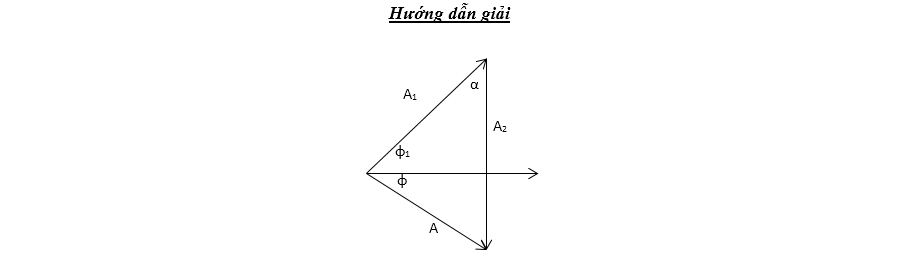
a. Ta biểu diễn các dao động bằng giản đồ véc tơ qauy như hình vẽ bên.
Áp
dụng định lý hàm số sin:
$\frac{{{A}_{2}}}{\sin
\left( \varphi +{{\varphi }_{1}} \right)}=\frac{A}{\sin \alpha }\Rightarrow
{{A}_{2}}=\frac{A\sin \left( \varphi +{{\varphi }_{1}} \right)}{\sin \alpha }$
Vì α, A
không đổi để A 2max khi và chỉ khi $\varphi +{{\varphi
}_{1}}=\frac{\pi }{2}\Rightarrow \varphi =\frac{\pi }{2}-{{\varphi
}_{1}}=\frac{\pi }{6}$
${{A}_{2m\text{ax}}}=\frac{A\sin
\left( \varphi +{{\varphi }_{1}} \right)}{\sin \alpha }=\frac{5}{\frac{1}{2}}=10cm$
b.
Phương trình dao động tổng hợp: $x=5\cos \left( 10\pi t+\frac{\pi }{6}
\right)cm$
c. Vận tốc của vật nặng: $v=\pm \omega \sqrt{{{A}^{2}}-{{x}^{2}}}=\pm $ 136,03cm/s
Bài
3: Hai chất điểm dao động điều hoà trên cùng một
trục tọa độ 0x, coi trong quá trình dao động hai chất điểm không va chạm vào
nhau. Biết phương trình dao động của hai chất điểm lần lượt là ${{x}_{1}}=4\cos \left( 4t+\frac{\pi }{3}
\right)cm$; ${{x}_{2}}=4\sqrt{2}c\text{os}\left( 4t+\frac{\pi }{12} \right)cm$,
a.
Trong quá trình dao động khoảng cách lớn nhất giữa hai vật là bao nhiêu.
b. Một vật thực hiện đồng thời hai dao động trên tìm phương trình dao động tổng hợp.

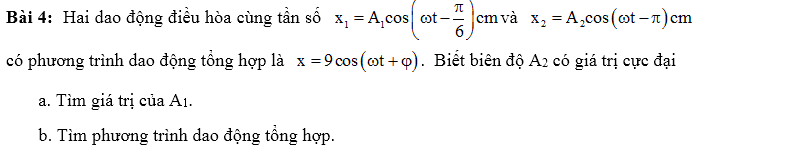
Theo định lý hàm số sin:
\[\frac{{{A}_{2}}}{\sin \alpha
}=\frac{A}{\sin \frac{\pi }{6}}\Rightarrow {{A}_{2}}=\frac{A\sin \alpha }{\sin
\frac{\pi }{6}}\]
A2
có giá trị cực đại khi sina = 1 $\Rightarrow $a = $\frac{\pi }{2}$
A2max = 2A = 18cm $\Rightarrow $ A1 = \[\sqrt{A_{2}^{2}-{{A}^{2}}}=\sqrt{{{18}^{2}}-{{9}^{2}}}=9\sqrt{3}\]cm
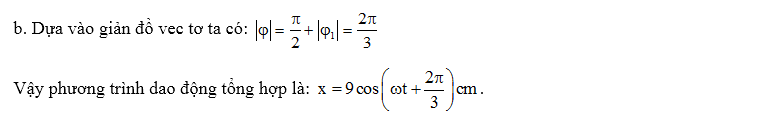

Theo định lý hàm số sin:
\[\frac{{{A}_{1}}}{\sin \alpha
}=\frac{A}{\sin (\pi -{{\varphi }_{2}})}\Rightarrow {{A}_{1}}=\frac{A\sin
\alpha }{\sin (\pi -{{\varphi }_{2}})}\]
A1
có giá trị cực đại khi sina = 1 $\Rightarrow
\alpha =\frac{\pi }{2}$
A1max = \[\sqrt{{{A}^{2}}+A_{2}^{2}}=\sqrt{2,{{5}^{2}}+3.2,{{5}^{2}}}=5cm\]
Khi
đó: $\sin \left( \pi -{{\varphi }_{2}} \right)=\frac{A}{{{A}_{1\max
}}}=\frac{1}{2}\Rightarrow \pi -{{\varphi }_{2}}=\frac{\pi }{6}\Rightarrow
{{\varphi }_{2}}=\frac{5\pi }{6}$
b.
Dựa vào giản đồ vec tơ ta có: $\varphi =\frac{\pi }{2}-\left( \pi -\frac{5\pi
}{6} \right)=\frac{\pi }{3}$
Vậy phương trình dao động tổng hợp là: $x=2,5\cos \left( \omega t+\frac{\pi }{3} \right)cm$
Bài
6: Một vật có khối lượng không đổi, thực hiện đồng
thời hai dao động điều hòa có phương trình dao động lần lượt là 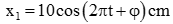 ; ${{x}_{2}}={{A}_{2}}\cos \left(
2\pi t-\frac{\pi }{2} \right)cm$thì dao động tổng hợp là $x=A\cos \left( 2\pi t-\frac{\pi }{3}
\right)cm$. Khi năng lượng dao động của vật cực đại thì biên độ dao động A2
có giá trị là bao nhiêu ?
; ${{x}_{2}}={{A}_{2}}\cos \left(
2\pi t-\frac{\pi }{2} \right)cm$thì dao động tổng hợp là $x=A\cos \left( 2\pi t-\frac{\pi }{3}
\right)cm$. Khi năng lượng dao động của vật cực đại thì biên độ dao động A2
có giá trị là bao nhiêu ?
Vẽ giãn đồ véc tơ
như hình vẽ : $\overrightarrow{A}={{\overrightarrow{A}}_{1}}+{{\overrightarrow{A}}_{2}}$
Theo định lí sin trong tam giác:\[\frac{A}{\sin
\alpha }=\frac{{{A}_{1}}}{\sin \frac{\pi }{6}}\Rightarrow A=\frac{{{A}_{1}}\sin
\alpha }{\sin \frac{\pi }{6}}\]
Amax khi $\sin \alpha =1\Rightarrow
\alpha =\frac{\pi }{2}\Rightarrow {{A}_{m\text{ax}}}=2{{A}_{1}}=20cm$
Năng lượng dao động của vật cực đại khi A
cực đại vậy: ${{\overrightarrow{A}}_{1}}\bot {{\overrightarrow{A}}_{2}}$
Suy ra A2 = \[\sqrt{{{A}^{2}}-A_{1}^{2}}\] = 10\[\sqrt{3}\] (cm).
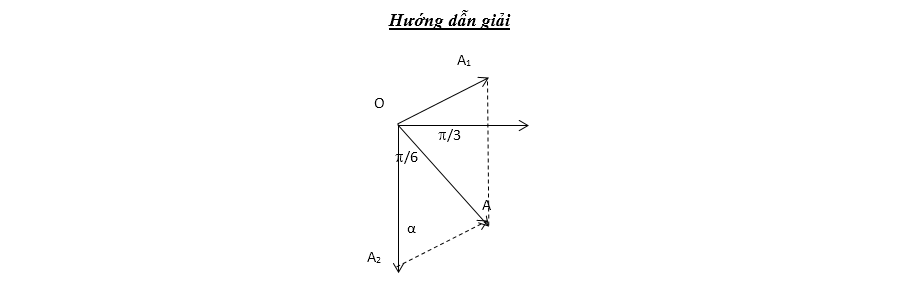
Bài 7: Hai dao động cùng phương lần lượt có phương trình ${{x}_{1}}={{A}_{1}}c\text{os}\left( \pi t+\frac{\pi }{6} \right)cm$ và ${{x}_{2}}=6\cos \left( \pi t-\frac{\pi }{2} \right)cm$. Dao động tổng hợp của hai dao động này có phương trình $x=A\cos (\pi t+\varphi )$cm. Thay đổi A1 cho đến khi biên độ A đạt giá trị cực tiểu thì pha ban đầu của dao động tổng hợp có giá trị bằng bao nhiêu ?
\[\frac{A}{\sin
\widehat{O{{A}_{2}}A}}=\frac{{{A}_{1}}}{\sin \widehat{OA{{A}_{2}}}}\Rightarrow
A=\frac{\sin \widehat{O{{A}_{2}}A}}{\sin
\widehat{OA{{A}_{2}}}}{{A}_{1}}=\frac{\sin {{60}^{0}}}{\sin
\widehat{OA{{A}_{2}}}}{{A}_{1}}\]
A đạt giá trị
cực tiểu khi \[\sin \widehat{OA{{A}_{2}}}=1\Rightarrow
\widehat{OA{{A}_{2}}}=\frac{\pi }{2}\]
Pha ban đầu của dao động tổng hợp: $\varphi =\frac{\pi }{2}-{{\varphi }_{1}}=\frac{\pi }{3}$
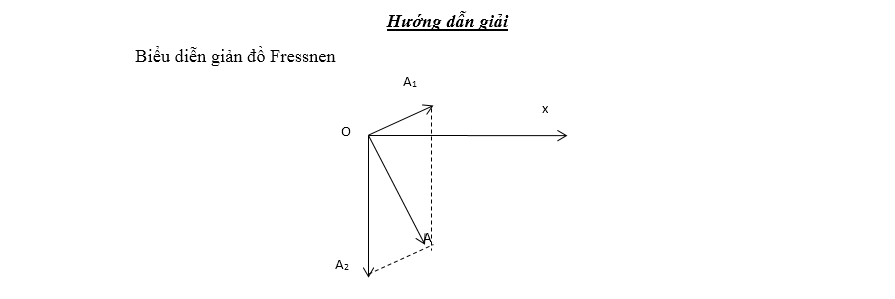
Bài 8: Hai dao động điều hòa cùng phương, cùng tần số, dao động
1 có biên độ A1= 10 cm, pha ban đầu p/6 và dao động 2
có biên độ A2, pha ban đầu -p/2. Biên độ A2 thay đổi được. Biên độ dao động
tổng hợp A có giá trị nhỏ nhất là bao nhiêu?
A. A = 2\[\sqrt{3}\] (cm) B. A= 5\[\sqrt{3}\] (cm) C. A = 2,5\[\sqrt{3}\] (cm) D. A= \[\sqrt{3}\] (cm)
Giải:
Ta biểu diễn các dao động bằng giản đồ véc tơ qauy như hình vẽ
bên:
Hình vẽ dễ dàng
ta thấy:
A min khi Biên độ dao động tổng hợp A trùng với
OM.
A= A1cos
(p/6) =10\[\sqrt{3}\]/2 = 5\[\sqrt{3}\] (cm).
Và A2 = A1sin (p/6) =10.1/2
= 5 (cm) => Chọn B
Bài 9: Một chất điểm thực hiện
đồng thời 2 dao đông điều hoà cung phương:
x1= A1cos(wt+p/3)(cm) và x2=
A2cos(wt- p/2)(cm).Phương trình
dao động tổng hợp là: x=5cos(wt+ j)(cm). Biên dộ dao động
A2 có giá trị lớn nhất khi j bằng bao nhiêu? Tính A2max?
A.- p/3; 8cm B.-p /6;10cm C.
p/6; 10cm D. B hoặc C
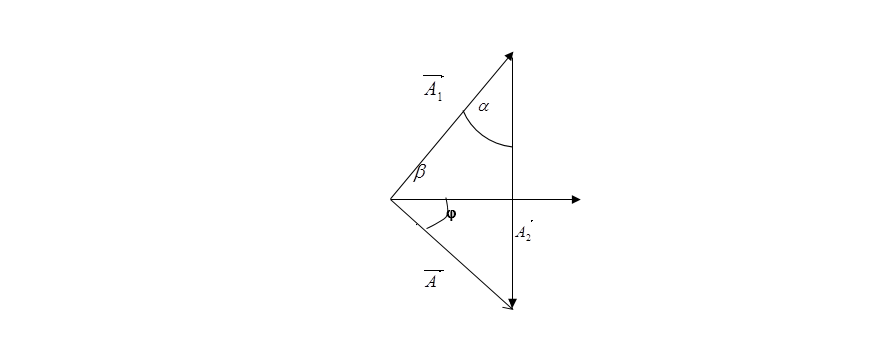
Giải:
Ta biểu diễn các dao động bằng giản đồ véc tơ qauy như hình vẽ
bên:
A2 max khi góc đối diện với nó ( góc b)
trong tam giác tạo bởi A1,A2,A là góc vuông
(tam giác vuông tại góc b
mà A2 là cạnh huyền)
Theo định lý hàm số sin ta có \[\frac{Sin\beta
}{{{A}_{2}}}=\frac{Sin\alpha }{A}\]=> \[{{A}_{2}}=Sin\beta
.\frac{A}{Sin\alpha }\].
Theo đề ta có A =5cm, a= p/6. Nên A2 phụ thuộc vào Sin b.
Trên hình vẽ: A2 max
khi góc đối diện b =p/2 =>\[{{A}_{2\max }}=1.\frac{A}{Sin{}^{\pi
}/{}_{6}}=\frac{5}{{}^{1}/{}_{2}}=10cm\]
Hình vẽ dễ dàng ta thấy: j = /b - j1
/= /
p/2
- p/3 / = p/6
Vì j <0 => j = - p/6
=> Chọn B
A. 4cm B. 6cm C. 8cm D. ( 4\[\sqrt{2}\]- 4)cm
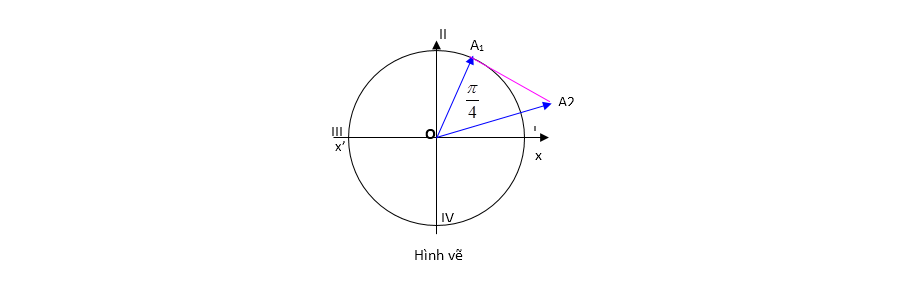
Giải:
(Xem hình vẽ 2 véctơ biểu diễn 2 dao động
thảnh phần )
Vì 2 dao động thành phần cùng tần số góc nên trong
quá trình các
Véc tơ quay tròn đều thì tam giác OA1A2
có độ lớn không đổi.
Độ lệch pha giữa 2 dao động thành phần : \[\frac{\pi
}{3}\]-\[\frac{\pi }{12}\]=\[\frac{\pi }{4}\]
Cạnh OA1 = 4cm ,OA2 = 4\[\sqrt{2}\]cm
, và góc A1OA2 =p/4
Dễ thấy góc OA1 A2 = p/2
và tam giác OA1A2 vuông cân tại A1.
Suy ra đoạn OA1 =A1A2 =
4cm (không đổi trong quá trình dao động)
A1A2
là khoảng cách giữa 2 vật .
Khi đoạn A1A2
song song với x’0x thi lúc đó khoảng
cách giữa hai vật chiếu
xuống trục x’ox
là lớn nhất và bằng 4cm => Chọn
A.







