Bài toán hay về sóng cơ

Câu 1:Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là u_A = u_B = acos20pt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A . Khoảng cách AM là
A. 5 cm. B. 2 cm. C. 4 cm. D. 2\[\sqrt{2}\] cm

Giải:

Bước sóng l = v/f = 4 cm

Xet điểm M: AM = d₁; BM = d₂

u_M = acos(20pt - \[\frac{2\pi {{d}_{1}}}{\lambda }\]) + acos(20pt - \[\frac{2\pi {{d}_{2}}}{\lambda }\])

u_M = 2acos(\[\frac{\pi ({{d}_{2}}-{{d}_{1}})}{\lambda }\]cos(20pt - \[\frac{\pi ({{d}_{1}}+{{d}_{2}})}{\lambda }\])

Điểm M dao độn với biên độ cực đại, cùng pha với nguồn A khi:cos(\[\frac{\pi ({{d}_{2}}-{{d}_{1}})}{\lambda }\] = 1 và \[\frac{\pi ({{d}_{1}}+{{d}_{2}})}{\lambda }\] = 2kp

=>. d₂ – d₁ = 2k’l

d₂ + d₁ = 2kl

=> d₁ = ïk – k’ïl. Điểm M gần A nhất ứng với k-k’ = 1=> d_1min = l = 4 cm. Đáp án C

Câu 2:Trong thí nghiệm giao thoa sóng, người ta tạo ra trên mặt nước hai nguồn sóng A,B dao động với phương trình u_A = u_B= 5cos\[10\pi t\]cm.Tốc độ truyền sóng trên mặt nước là 20cm/s.Một điểm N trên mặt nước với AN – BN = - 10cm nằm trên đường cực đại hay cực tiểu thứ mấy, kể từ đường trung trực của AB?

A. Cực tiểu thứ 3 về phía A B. Cực tiểu thứ 4 về phía A

C. Cực tiểu thứ 4 về phía B D. Cực đại thứ 4 về phía A

Giải:

Bước sóng l = v/f = 4 cm

AN – BN = = d₁ – d₂ = - 10 cm = - 2,5l = ( - 3 + 0,5)l

Do đó điểm N nằm trên đường cực tiểu thứ 3 về phía A kể từ đường trung trực. Chọn đáp án A

Câu 3:Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn S₁S₂ = 9λ phát ra dao động u=cos(20pt). Trên đoạn S₁S₂, số điểm có biên độ cực đại cùng pha với nhau và ngược pha với nguồn (không kể hai nguồn) là:

A. 8. B. 9 C. 17. D. 16.

Giải:Phương trình sóng tổng quát tổng hợp tại M là: u_M = 2cos(p\[\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }\])cos(20pt - p\[\frac{{{d}_{2}}+{{d}_{1}}}{\lambda }\])

Với d₁ + d₂ = S₁S₂ = 9λ

Khi đó: Phương trình sóng tổng quát tổng hợp tại M là:

u_M = 2cos(p\[\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }\])cos(20pt - 9p) = 2cos(p\[\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }\])cos(20pt - p) = - 2cos(p\[\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }\])cos(20pt)

Vậy sóng tại M ngược pha với nguồn khi cos(p\[\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }\]) = 1 Û p\[\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }\] = k2p Û d₁ - d₂ = 2kl

Với - S₁S₂ £ d₁ - d₂£ S₁S₂ Û -9l £ 2kl £ 9lÛ 4,5 £ k £ 4,5

Suy ra k = 0; ±1, ±2; ±3; ±4. Có 9 giá trị (có 9 cực đại)

Câu 4:Hai điểm M, N cùng nằm trên một phương truyền sóng cách nhau l/3. Tại thời điểm t, khi li độ dao động tại M là u_M= + 3 cm thì li độ dao động tại N là u_N = - 3 cm. Biên độ sóng bằng :

A. A = $\sqrt{6}$cm. B. A = 3 cm. C. A = 2$\sqrt{3}$cm. D. A = 3$\sqrt{3}$cm.

HD: Trong bài MN = l/3 (gt) Þ dao động tại M và N lệch pha nhau một góc 2p/3. Giả sử dao động tại M sớm pha hơn dao động tại N.

Cách 1: (Dùng phương trình sóng)

Ta có thể viết: u_M = Acos(wt) = +3 cm (1), u_N = Acos(wt - $\frac{2\pi }{3}$) = -3 cm (2)

+ (2) Þ A[cos(wt) + cos(wt - $\frac{2\pi }{3}$)] = 0. Áp dụng : cosa + cosb = 2cos$\frac{a+b}{2}$cos$\frac{a-b}{2}$

Þ 2Acos$\frac{\pi }{3}$cos(wt -$\frac{\pi }{3}$) = 0 Þ cos(wt -$\frac{\pi }{3}$) = 0 Þ wt -$\frac{\pi }{3}$ = $\frac{\pi }{2}+k\pi $, k Î Z. Þ wt = $\frac{5\pi }{6}$+ kp, k Î Z.

Thay vào (1), ta có: Acos($\frac{5\pi }{6}$+ kp) = 3. Do A > 0 nên Acos($\frac{5\pi }{6}$- p) = Acos(-$\frac{\pi }{6}$) = $\frac{A\sqrt{3}}{2}$ = 3 (cm)

Þ A = 2$\sqrt{3}$cm

Cách 2: (Dùng liên hệ giữa dao động điều hòa và chuyển động tròn đều:

$\overrightarrow{ON'}$ (ứng với u_N) luôn đi sau véctơ $\overrightarrow{OM'}$ (ứng với u_M) và chúng hợp với nhau một góc Dj = $\frac{2\pi }{3}$ (ứng với MN = $\frac{\lambda }{3}$, dao động tại M và N lệch pha nhau một góc $\frac{2\pi }{3}$)

Do vào thời điểm đang xét t, u_M = + 3 cm, u_N = -3 cm (Hình), nên ta có

N’OK = KOM’ = $\frac{\Delta \varphi }{2}$ = $\frac{\pi }{3}$ Þ Asin$\frac{\pi }{3}$ = 3 (cm) Þ A = 2$\sqrt{3}$cm.

Câu 5:Hai điểm M, N cùng nằm trên một phương truyền sóng cách nhau l/3. Tại thời điểm t, khi li độ dao động tại M là u_M = +3 cm thì li độ dao động tại N là u_N = 0 cm. Biên độ sóng bằng :

A. A = $\sqrt{6}$cm. B. A = 3 cm. C. A = 2$\sqrt{3}$cm. D. A = 3$\sqrt{3}$cm.

HD: Trong bài MN = l/3 (gt) Þ dao động tại M và N lệch pha nhau một góc 2p/3. Giả sử dao động tại M sớm pha hơn dao động tại N.

Cách 1: (Dùng phương trình sóng)

Ta có thể viết: u_M = Acos(wt) = +3 cm (1), u_N = Acos(wt - $\frac{2\pi }{3}$) = 0 cm (2)

Từ (2) Þ cos(wt - $\frac{2\pi }{3}$) = 0 Þ wt - $\frac{2\pi }{3}$ = $\frac{\pi }{2}+k\pi $, k Î Z Þ wt = $\frac{7\pi }{6}$+ kp, k Î Z.

Thay vào (1): Acos($\frac{7\pi }{6}$+ kp) = 3. Do A > 0 nên Acos($\frac{7\pi }{6}$- p) = Acos($\frac{\pi }{6}$) = $\frac{A\sqrt{3}}{2}$ = 3 (cm) Þ A = 2$\sqrt{3}$cm.

Câu 6:Nguồn sóng ở O dao động với tần số 10 Hz , dao động truyền đi với vận tốc 0,4 m/s trên phương Ox . Trên phương này có 2 điểm P và Q theo chiều truyền sóng với PQ = 15 cm. Cho biên độ sóng a = 1 cm và biên độ không thay đổi khi sóng truyền. Nếu tại thời điểm nào đó P có li độ 1 cm thì li độ tại Q là:

A. 1 cm B. – 1 cm C. 0 D. 0,5 cm

HD: Tính được l = 4 cm ; $\frac{PQ}{\lambda }$ = 3,75 hay PQ = 3l + 0,75l ; Dj = 2p.$\frac{PQ}{\lambda }$ = 7,5p hay Dj = 0,75.2p = $\frac{3\pi }{2}$

(Nhớ: Ứng với khoảng cách l thì độ lệch pha là 2p ; ứng với 0,75l thì Dj = 0,75.2p = $\frac{3\pi }{2}$).

Þ dao động tại P sớm pha hơn dao động tại Q một góc $\frac{3\pi }{2}$ hay dao động tại P trễ pha hơn dao động tại Q một góc $\frac{\pi }{2}$.

Þ Lúc u_P = 1 cm = a thì u_Q = 0.

Câu 7:Một sóng cơ học lan truyền trên mặt thoáng chất lỏng nằm ngang với tần số 10 Hz, tốc độ truyền sóng 1,2 m/s. Hai điểm M và N thuộc mặt thoáng, trên cùng một phương truyền sóng, cách nhau 26 cm (M nằm gần nguồn sóng hơn). Tại thời điểm t, điểm N hạ xuống thấp nhất. Khoảng thời gian ngắn nhất sau đó điểm M hạ xuống thấp nhất là

A. \[11/120s.\] B. \[1/60s.\] C. \[1/120s.\] D. \[1/12s.\]

HD: l = 12 cm ; $\frac{MN}{\lambda }$ = $\frac{26}{12}$= 2 + $\frac{1}{6}$ hay MN = 2l + $\frac{\lambda }{6}$ Þ Dao động tại M sớm pha hơn dao động tại N một góc $\frac{\pi }{3}$.Þ Dùng liên hệ giữa dao động điều hòa và chuyển động tròn đều dễ dàng thấy : Ở thời điểm t, u_N = -a (xuống thấp nhất) thì u_M = $-\frac{a}{2}$ và đang đi lên.Þ Thời gian Dt_min = $\frac{5T}{6}$= $\frac{5}{60}s=\frac{1}{12}s$, với T =$\frac{1}{f}=\frac{1}{10}s$.

Câu 7:Một sóng cơ học lan truyền trên mặt thoáng chất lỏng nằm ngang với tần số 10 Hz, tốc độ truyền sóng 1,2 m/s. Hai điểm M và N thuộc mặt thoáng, trên cùng một phương truyền sóng, cách nhau 26 cm (M nằm gần nguồn sóng hơn). Tại thời điểm t, điểm M hạ xuống thấp nhất. Khoảng thời gian ngắn nhất sau đó điểm N hạ xuống thấp nhất là

A. \[11/120s.\] B. \[1/60s.\] C. \[1/120s.\] D. \[1/12s.\]

Þ Thời gian Dt_min = $\frac{T}{6}$= $\frac{1}{60}s$, với T =$\frac{1}{f}=\frac{1}{10}s$.

Câu 8:Tại hai điểm A và B trên mặt nước có 2 nguồn sóng cùng pha, biên độ lần lượt là 4cm và 2cm, bước sóng là 10cm. Điểm M trên mặt nước cách A 25cm và cách B 30cm sẽ dao động với biên độ là

A. 2cm B. 4cm C. 6cm D. 8cm

Giải : Hai nguồn sóng cùng pha, biên độ khác nhau, cùng bước sóng trên mặt nước nên cùng tần số.

+Phương trình sóng tại 2 nguồn:(Điểm M cách hai nguồn lần lượt d₁, d₂)

${{u}_{1}}={{\text{A}}_{1}}\text{cos}(2\pi ft+{{\varphi }_{1}})$ và ${{u}_{2}}={{\text{A}}_{2}}\text{cos}(2\pi ft+{{\varphi }_{2}})$

+Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

${{u}_{1M}}={{\text{A}}_{1}}\text{cos}(2\pi ft-2\pi \frac{{{d}_{1}}}{\lambda }+{{\varphi }_{1}})$ và ${{u}_{2M}}={{\text{A}}_{2}}\text{cos}(2\pi ft-2\pi \frac{{{d}_{2}}}{\lambda }+{{\varphi }_{2}})$

Do nguồn cùng pha và đề cho A₁ = 2A₂thì:

${{u}_{1M}}=2{{\text{A}}_{2}}\text{cos}(2\pi ft-2\pi \frac{{{d}_{1}}}{\lambda })$ và ${{u}_{2M}}={{\text{A}}_{2}}\text{cos}(2\pi ft-2\pi \frac{{{d}_{2}}}{\lambda })$

Thế số: ${{u}_{1M}}=4\text{cos}(2\pi ft-2\pi \frac{25}{10})$ và ${{u}_{2M}}=2\text{cos}(2\pi ft-2\pi \frac{30}{10})$

<=> ${{u}_{1M}}=4\text{cos}(2\pi ft-5\pi )$ và ${{u}_{2M}}=2\text{cos}(2\pi ft-6\pi )$

Vì hàm cosin có chu kỳ 2p nên ta viết lại: ${{u}_{1M}}=4\text{cos}(2\pi ft-\pi )$ và ${{u}_{2M}}=2\text{cos}(2\pi ft)$

-Phương trình giao tổng hợp sóng tại M: u_M = u_1M + u_2M:

Dễ thấy hai dao động ngược pha nên biên độ tổng hợp tại M là trừ nhau: A = / 4-2 / =2 cm. Chọn A

Câu 9:Hai nguồn sóng kết hợp cách nhau 11cm dao động với cùng phương trình \[u=a\cos 20\pi t\ \left( mm \right)\] trên mặt nước, sóng lan truyền với tốc độ v = 0,4m/s và biên độ không đổi khi truyền đi. Hỏi điểm gần nhất dao động ngược pha với nguồn trên đường trung trực của \[{{S}_{1}}{{S}_{2}}\] cách các nguồn bao nhiêu

A. 5,5 cm

B. 11 cm

C. 8 cm

D. 6 cm

HD: Phương trình dao động tại trung trực \[u=2a\cos (20\pi t-\frac{2\pi d}{\lambda }),do:{{d}_{1}}={{d}_{2}}=d\]

Dao động ngược pha nên: \[\Delta \phi =\frac{2\pi d}{\lambda }=(2k+1)\pi \Rightarrow d=\frac{(2k+1)\lambda }{2},do:d\ge \frac{{{S}_{1}}{{S}_{2}}}{2}\Rightarrow {{d}_{\min }}=6cm\]

Câu 10: Tại hai điểm A và B trên mặt chất lỏng có hai nguồn phát sóng cơ đồng bộ cách nhau AB = 8cm, dao động với tần số f = 20Hz và pha ban đầu bằng 0. Một điểm M trên mặt nước, cách A một khoảng 25 cm và cách B một khoảng 20,5 cm, dao động với biên độ cực đại. Giữa M và đường trung trực của AB có hai vân giao thoa cực đại. Coi biên độ sóng truyền đi không giảm.

1. Xác định tốc độ truyền sóng và tìm số điểm dao động cực đại, số điểm dao động cực tiểu trên đoạn AB (không kể A và B).

2. Gọi O là trung điểm của AB; N và P là hai điểm nằm trên trung trực của AB về cùng một phía so với O thỏa mãn ON = 2cm; OP = 5cm. Xác định các điểm trên đoạn NP dao động cùng pha với O.

3. Điểm Q cách A khoảng L thỏa mãn AQ $\bot $ AB.

a) Tính giá trị cực đại của L để điểm Q dao động với biên độ cực đại.

b) Xác định L để Q đứng yên không dao động

Giải:

1. Điều kiện để tại M dao động cực đại: \[{{d}_{2}}-{{d}_{1}}=k.\lambda \to k\lambda =25-20,5=4,5\] (cm)

Vì giữa M và đường trung trực của AB có 2 vân giao thoa cực đại. Tại M là vân dao thoa cực đại thứ 3 nên k = 3. Từ đó \[\to \lambda =1,5(cm)\]

Mà: v = \[\lambda \].f = 20.1,5 = 30 (cm/s)

- Đk để tại M’ trên AB có dao động cực đại:

d₂ – d₁ = k. \[\lambda \] (với k = 0; \[\pm \]1; \[\pm \]2; \[\pm \] 3 ..)

d₁+ d₂ = AB nên: d₁ = \[\frac{1}{2}(k\lambda +AB)\]

0 < d₁; d₂ < AB hay 0 < \[\frac{1}{2}(k\lambda +AB)\]< AB

Thay số vào tìm được: - \[\frac{AB}{\lambda }\]< k < \[\frac{AB}{\lambda }\] hay: -5,33 < k < 5,33.

Vậy: k = -5, -4, -3, -2, -1,0, 1, 2, 3, 4, 5.

Vậy trên đoạn AB có 5.2 + 1 = 11 điểm dao động cực đại.

- Đk tại M’ trên AB có dao động cực tiểu:

d₂ – d₁ = (2k+1) \[\frac{\lambda }{2}\] (với k = 0; \[\pm \]1; \[\pm \]2; \[\pm \] 3 ..)

d₁+ d₂ = AB nên: d₁ = \[(2k+1)\frac{1}{4}\lambda +\frac{1}{2}AB\]

0 < d₁; d₂ < AB hay 0 < \[(2k+1)\frac{1}{4}\lambda +\frac{1}{2}AB\]< AB

Thay số: -5,83 < k < 4,83 nên: k = -5, -4, -3, -2, -1,0, 1, 2, 3, 4.

Như vậy có 10 giá trị của k nên trên đoạn AB có 10 cực tiểu.

2. Phương trình dao động của hai nguồn: u₁ = u₂ = Acos2pft

Điểm T nằm trên trung trực của AB cách A khoảng d dao động theo phương trình: u = 2Acos(2pft - p\[\frac{d}{\lambda }\])

Độ lệch pha của điểm này so với O: Dj = 2p\[\frac{d-{{d}_{O}}}{\lambda }\]

Điều kiện để điểm này dao động cùng pha với O: Dj = k2p (k nguyên)

® d - d_O = kl ® d = d_O + kl = 4 + 1,5k (cm)

Nếu T nằm trên đoạn NP: d_N \[\le \] 4 + 1,5k \[\le \] d_P

® \[\sqrt{d_{O}^{2}+O{{N}^{2}}}\]\[\le \] 4 + 1,5k \[\le \]\[\sqrt{d_{O}^{2}+O{{P}^{2}}}\]® 0,31 \[\le k\le \] 1,60 ® k = 1

® d = 5,5cm ® OT = \[\sqrt{{{d}^{2}}-d_{O}^{2}}\] =3,8cm.

Vậy điểm T trên trung trực AB cách O 3,8cm dao động cùng pha với O

3. a. Điều kiện để tại Q có cực đại giao thoa là hiệu đường đi từ Q đến hai nguồn sóng phải bằng số nguyên lần bước sóng: \[\sqrt{{{L}^{2}}+{{a}^{2}}}-L=k\lambda .\]; k=1, 2, 3... và a = AB

Khi L càng lớn đường AQ cắt các cực đại giao thoa có bậc càng nhỏ (k càng bé), vậy ứng với giá trị lớn nhất của L để tại Q có cực đại nghĩa là tại Q đường AQ cắt đường cực đại bậc 1 (k = 1).

Thay các giá trị đã cho vào biểu thức trên ta nhận được: \[\sqrt{L_{m\text{ax}}^{2}+64}-L_{m\text{ax}}^{{}}=1,5\Rightarrow {{L}_{m\text{ax}}}=20,6(cm)\]

b. Điều kiện để tại Q có cực tiểu giao thoa là: \[\sqrt{{{L}^{2}}+{{d}^{2}}}-L=(2k+1)\frac{\lambda }{2}.\] (k=0, 1, 2, 3, ...)

Ta suy ra : \[L=\frac{{{d}^{2}}-{{\left[ (2k+1)\frac{\lambda }{2} \right]}^{2}}}{(2k+1)\lambda }\]

L > 0 ® k < 4,8 ® k = 0; 1; 2; 3; 4. Từ đó ta có 5 giá trị của L là:

* Với k = 0 thì L = 42,29cm;* Với k = 1 thì L = 13,10cm

* Với k = 2 thì L = 6,66cm; * Với k = 3 thì L = 3,47cm

* Với k = 4 thì L = 1,37cm

Câu 11:Trên mặt nước có hai nguồn sóng nước A và B cách nhau 16cm đang dao động vuông góc với mặt nước có cùng phương trình x = acos50pt (cm). Biết C là một điểm trên mặt nước, thuộc đường cực tiểu, giữa C và đường trung trực của đoạn AB có một đường cực đại. Khoảng cách AC = 17,2cm; BC = 13,6cm.

a/ Tính bước sóng và vận tốc truyền sóng trên mặt nước?

b/ Trên cạnh AC có mấy điểm dao động với biên độ cực đại (không kể hai điểm A và C) ?

Giải:

a. Tần số góc ω = 50π => f = 25 Hz

Tại C: d₁ - d₂ = (2k+1).\[\frac{\lambda }{2}\] (hình bên)

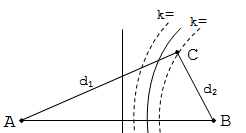
Theo đề: k = 1 Þ λ = 2,4cm.

Þ v = λ.f = 60cm/s

b. Số điểm dao động với biên độ cực đại trên đoạn AB?

d₁ – d₂ = kλ

d₁ + d₂ = AB => d₁ = 1,2k + 8

mà 0 < d₁ < 16 => - 6,7 < k < 6,7

Vậy có 13 điểm dao động với biên độ cực đại trên đoạn AB

=> Số đường cực đại đi qua AC là: 8.

Câu 12:Hai nguồn sáng S1 ,S2 dao động cùng pha cách nhau 8 cm về một phía của S1 S2 lấy hai điểm S3 S4 sao cho S3 S4 bằng 4cm và hợp thành hình thang cân S1 S2 S3 S4 .biết bước sóng của sóng trên mặt nước là 1 cm. Hỏi đường cao lớn nhất của hình thanh là bao nhiêu để trên đoạn S3 S4 có 5 điểm dao động cực đại

Giải:

Để trên S₃S₄ có 5 điểm dao động cự đại thì tại S₃,S₄ là dao động cực đai thứ hai tức là k = ± 2

d₁ = S₁S₃; d₂ = S₂S₃

d₁ – d₂ = 2l = 2 cm (*)

d₁² = h² + 6² d₂² = h² + 2^2‑

d₁² – d² = 32 (**)

Từ (*) và (**) suy ra :d₁ + d₂ = 16 cm => d₁ = 9cm

=> h = \[\sqrt{{{9}^{2}}-{{6}^{2}}}\]= 3\[\sqrt{5}\] = 6,71 cm

Câu 12:Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp S₁ và S₂ cách nhau 20cm. Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là u₁ = 3 cos25pt (mm) và u₂ = 4sin(25pt) (mm). Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. Những điểm M thuộc mặt nước có hiệu đường đi d = | S₁M – S₂M| = 2k (cm) (với k = 0, 1,2 ,3, ...) sẽ dao động với biên độ bằng

A. 7 mm. B. 5 mm. C.1 mm. D. 6 mm.

Giải: Ta có phương trình sóng tại M do S1 và S2 gây ra:

\[{{u}_{1M}}=3\cos (25\pi t-25\pi \frac{M{{S}_{1}}}{v})v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }{{\text{u}}_{2M}}=4\cos (25\pi t-25\pi \frac{M{{S}_{2}}}{v}-\frac{\pi }{2})\]

Biên độ sóng tổng hợp tại M: $\begin{aligned}

& a_{M}^{2}=9+16+24\sin 25\pi \frac{M{{S}_{1}}-M{{S}_{2}}}{v}=25+24\sin 25\pi \frac{2k}{0,5}=25 \\

& \Rightarrow {{a}_{M}}=5mm \\

\end{aligned}$

Câu 13:Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp A, B cách nhau 10 cm, dao động theo phương thẳng đứng với phương trình lần lượt là u_A = 3cos(40pt +p/6) (cm); u_B = 4cos(40pt + 2p/3) (cm). Cho biết tốc độ truyền sóng là 40 cm/s. Một đường tròn có tâm là trung điểm của AB, nằm trên mặt nước, có bán kính R = 4cm. Số điểm dao động với biên độ 5 cm có trên đường tròn là

A. 30 B. 32 C. 34 D. 36

Giải:Phương trình sóng tại M do sóng tại A truyền đến là:

u_AM = 3cos(40pt + \[\frac{\pi }{6}\] - \[\frac{2\pi {{d}_{1}}}{\lambda }\])

Phương trình sóng tại M do sóng tại B truyền đến là:

u_BM = 4cos(40pt + \[\frac{2\pi }{3}\] - \[\frac{2\pi {{d}_{2}}}{\lambda }\])

Phương trình sóng tổng quát tổng hợp tại M là:

u_M = u_AM + u_BM = 3cos(40pt + \[\frac{\pi }{6}\] - \[\frac{2\pi {{d}_{1}}}{\lambda }\]) + 4cos(40pt + \[\frac{2\pi }{3}\] - \[\frac{2\pi {{d}_{2}}}{\lambda }\])

Biên độ sóng tổng hợp tại M là: (Áp dụng công thức dao động điều hòa)

A = \[\sqrt{{{3}^{2}}+{{4}^{2}}+2.3.4.c\text{os}(\frac{2\pi }{3}-\frac{2\pi {{d}_{2}}}{\lambda }-(\frac{\pi }{6}-\frac{2\pi {{d}_{1}}}{\lambda }))}\]

=\[\sqrt{{{3}^{2}}+{{4}^{2}}+2.3.4.c\text{os}(\frac{\pi }{2}-\frac{2\pi }{\lambda }({{d}_{2}}-{{d}_{1}}))}\]

Biên độ sóng tổng hợp tại M bằng 5 khi: \[c\text{os}(\frac{\pi }{2}-\frac{2\pi }{\lambda }({{d}_{2}}-{{d}_{1}}))\]= 0

Khi đó: \[\frac{\pi }{2}-\frac{2\pi }{\lambda }({{d}_{2}}-{{d}_{1}})\]\[\frac{\pi }{2}-2\pi (\frac{{{d}_{2}}}{\lambda }-\frac{{{d}_{1}}}{\lambda }\]) = \[\frac{\pi }{2}-k\pi \]

Do đó: d₂ – d₁ = k\[\frac{\lambda }{2}\]; Mà - 8 £ d₂ – d₁ £ 8 Û - 8 £ k\[\frac{\lambda }{2}\] £ 8 Û - 8 £ k £ 8

Tương tự tại hai điểm M và N ở hai đầu bán kính là điểm dao động với biên độ bằng 5cm

Nên số điểm dao động với biên độ 5cm là: n = 17x2 – 2 = 32

Câu 14:Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha, cùng tần số, cách nhau AB = 8cm tạo ra hai sóng kết hợp có bước sóng l = 2cm. Trên đường thẳng (D) song song với AB và cách AB một khoảng là 2cm, khoảng cách ngắn nhất từ giao điểm C của (D) với đường trung trực của AB đến điểm M dao động với biên độ cực tiểu là

A. 0,43 cm. B. 0,5 cm. C. 0,56 cm. D. 0,64 cm.

Giải:

M dao động cực tiểu gần C nhất nên M thuộc cực tiểu k = 0

Lúc đó: d₁ – d₂ = (k+ $\frac{1}{2}$) λ = $\frac{1}{2}$λ (1)

Gọi x là khoảng cách từ M đến C:

${{d}_{1}}=\sqrt{{{(AI+x)}^{2}}+M{{K}^{2}}}\,$;

${{d}_{2}}=\sqrt{{{(BI-x)}^{2}}+M{{K}^{2}}}\,$

thay vào (1):

${{d}_{1}}-{{d}_{2}}=\sqrt{{{(AI+x)}^{2}}+M{{K}^{2}}}\,-\sqrt{{{(BI-x)}^{2}}+M{{K}^{2}}}=\frac{\lambda }{2}$

Thay số vào giải pt: ${{d}_{1}}-{{d}_{2}}=\sqrt{{{(4+x)}^{2}}+{{2}^{2}}}\,-\sqrt{{{(4-x)}^{2}}+2}=1\,\,\,\,\,=>\,x=0,56cm$ Chọn C

Câu 15:Có hai nguồn dao động kết hợp S₁ và S₂ trên mặt nước cách nhau 8cm có phương trình dao động lần lượt là u_s1 = 2cos(10pt - \[\frac{\pi }{4}\]) (mm) và u_s2 = 2cos(10pt + \[\frac{\pi }{4}\]) (mm). Tốc độ truyền sóng trên mặt nước là 10cm/s. Xem biên độ của sóng không đổi trong quá trình truyền đi. Điểm M trên mặt nước cách S₁ khoảng S₁M=10cm và S₂ khoảng S₂M = 6cm. Điểm dao động cực đại trên S₂M xa S₂ nhất là

A. 3,07cm. B. 2,33cm. C. 3,57cm. D. 6cm.

Giải: Bước sóng λ = v/f = 2cm

Xét điểm C trên BN: S₁N = d₁; S₂N = d₂ ( 0≤ d₂ ≤ 6 cm)

Tam giác S₁S₂M là tam giác vuông tại S₂

Sóng truyền từ S₁; S₂ đến N:u_1N = 2cos(10pt - \[\frac{\pi }{4}\] - \[\frac{2\pi {{d}_{1}}}{\lambda }\]) (mm)

u_2N = 2cos(10pt + \[\frac{\pi }{4}\] - \[\frac{2\pi {{d}_{2}}}{\lambda }\]) (mm)

u_N = 4 cos[\[\frac{\pi ({{d}_{1}}-{{d}_{2}})}{\lambda }\]- \[\frac{\pi }{4}\]] cos[10πt -\[\frac{\pi ({{d}_{1}}+{{d}_{2}})}{\lambda }\]]

N là điểm có biên độ cực đại: cos[\[\frac{\pi ({{d}_{1}}-{{d}_{2}})}{\lambda }\]- \[\frac{\pi }{4}\]] = ± 1 =>[\[\frac{\pi ({{d}_{1}}-{{d}_{2}})}{\lambda }\]- \[\frac{\pi }{4}\]] = kπ

\[\frac{{{d}_{1}}-{{d}_{2}}}{2}\]- \[\frac{1}{4}\] = k => d₁ – d₂ = \[\frac{4k-1}{2}\] (1)

d₁² – d₂² = S₁S₂² = 64 => d₁ + d₂ = \[\frac{64}{{{d}_{1}}-{{d}_{2}}}=\frac{128}{4k-1}\] (2)

(2) – (1) Suy ra d₂ = \[\frac{64}{4k-1}-\frac{4k-1}{4}\]= \[\frac{256-{{(4k-1)}^{2}}}{4(4k-1)}\] k nguyên dương

à 0 ≤ d₂ ≤ 6 à 0 ≤ d₂ = \[\frac{256-{{(4k-1)}^{2}}}{4(4k-1)}\] ≤ 6 đặt X = 4k-1

=> 0 ≤ \[\frac{256-{{X}^{2}}}{4X}\] ≤ 6 => X ≥ 8 => 4k – 1 ≥ 8 => k ≥3

Điểm N có biên độ cực đại xa S₂ nhất ứng với giá trị nhỏ nhất của k: k_min = 3

Khi đó d₂ =\[\frac{256-{{(4k-1)}^{2}}}{4(4k-1)}=\frac{256-{{11}^{2}}}{44}=3,068\approx 3,07\] (cm) .Chọn đáp án A