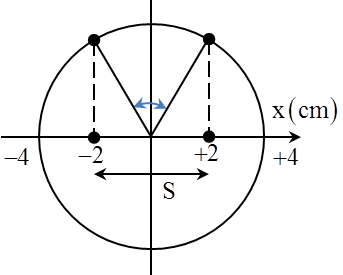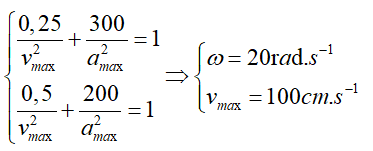BÀI TẬP DÙNG VTLG TRONG DAO ĐỘNG ĐIỀU HÒA
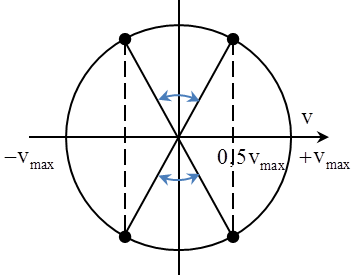
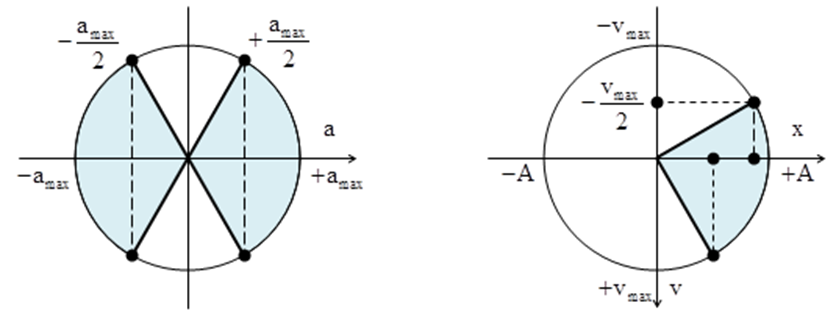
Câu 1 : Trong dao động điều hòa của một vật. Khoảng thời gian trong một chu kì để vận tốc của vật có độ lớn \[\left| v \right|\le 0,5{{v}_{m\text{ax}}}\]là :
A. \[\frac{T}{3}\] B. \[\frac{T}{4}\] C. \[\frac{T}{5}\] D. \[\frac{T}{6}\]
Hướng dẫn
|
Từ hình vẽ ta xác định được \[t=\frac{T}{3}\]
|
|
Câu 2 : Xác định thời gian để vật đi qua vị trí gia tốc cực tiểu lần thứ 2 kể từ thời điểm ban đầu. Biết rằng ban đầu vật đang ở vị trí biên âm và vật dao động với chu kì 4s.
A. 5 s B. 6 s C. 10 s D. 12 s
Hướng dẫn
Gia tốc của vật cực đại tại vị trí biên dương, vật vật sẽ mất 1,5T = 6 s để đi qua vị trí này hai lần
- Đáp án B
Câu 3 : Một vật dao động điều hòa với biên độ A và tần số góc π rad/s. Thời gian ngắn nhất trong một chu kì để hai lần liên tiếp vật đi qua vị trí có động năng bằng 3 lần thế năng :
A. \[\frac{2}{3}\] s B. \[\frac{1}{3}\] s C. 1 s D. 2 s
Hướng dẫn
Động năng của vật bằng ba lần thế năng tại vị trí \[x=\pm \frac{A}{2}\]\[\Rightarrow \]Khoảng thời gian ngắn nhất trong một chu kì vật đi qua hai vị trí này là \[\frac{T}{6}=\frac{1}{3}s\]
- Đáp án B
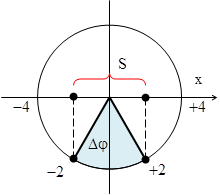
Câu 4 : Biết rằng trong một chu kì quãng đường mà vật dao động điều hòa đi được là 20 cm, tần số góc của dao động là π rad/s. Thời gian để vật từ vị trí biên âm đi qua vị trí vật có vận tốc 5π rad/s lần đầu tiên là :
A. 1 s B. 2 s C. 0,5 s D. 0,25 s
Hướng dẫn
Quãng đường mà vật đi được trong một chu kì là\[S=4A=20\Rightarrow A=5cm\], tốc độ cực đại của dao động
Thời gian để vật đi từ biên âm đến vị trí có tốc độ cực đại là \[t=\frac{T}{4}=0,5s\]
- Đáp án C
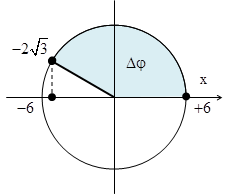
Câu 5: Phương trình li độ của một vật dao động điều hòa được cho bởi \[x=4\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm (t tính bằng s). Quãng đường mà vật đi được từ thời điểm ban đầu đến vị trí mà gia tốc của vật bằng một nửa gia tốc cực đại lần đầu tiên
A. 4 cm B. 2 cm C. 8 cm D. 16 cm
Hướng dẫn
|
+ Tại thời điểm ban đầu vật đi qua vị trí \[x=2\] cm theo chiều âm + Gia tốc của vật bằng một nửa gia tốc cực đại tại vị trí \[x=-\frac{A}{2}=-2cm\] Từ hình vẽ, ta có quãng đường tương ứng \[S=4cm\]
|
|
Câu 6: Một vật dao động điều hòa theo phương trình \[x=5\cos \left( \pi t+\frac{\pi }{2} \right)\]cm (t được tính bằng s). Quãng đường lớn nhất mà vật đi được trong \[\frac{2}{3}\] s là :
A. 5 cm B. \[5\sqrt{2}\]cm C. \[5\sqrt{3}\]cm D. 6 cm
Hướng dẫn
Chu kì dao động của vật \[T=\frac{2\pi }{\omega }=2s\]
Quãng đường lớn nhất mà vật đi được trong \[\frac{2}{3}s\]
\[{{S}_{max}}=2Asin\left( \frac{\omega \Delta t}{2} \right)=2.5.\sin \left( \frac{\pi .\frac{2}{3}}{2} \right)=5\sqrt{3}cm\]
- Đáp án C
Câu 7 : Một con lắc gồm lò xo có độ cứng 100 N/m, vật nặng có khối lượng 100 g dao động điều hòa với biên độ 4 cm. Tốc độ trung bình của vật khi nó đị từ vị trí biên dương đến vị trí động năng bằng 3 lần thế năng lần thứ 2 là :
A. 75 cm/s B. 80 cm/s D. 90 cm/s D. 100 cm/s
Hướng dẫn
|
+ Tần số góc và chu kì của dao động
\[\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{100}{{{100.10}^{-3}}}}=10\pi rad.{{s}^{-1}}\] \[T=\frac{2\pi }{\omega }=0,2s\] + Vị trí động năng bằng 3 lần thế năng \[x=\pm \frac{A}{2}\] + Từ hình vẽ ta có \[{{v}_{tb}}=\frac{S}{t}=\frac{8+2}{2.\frac{0,2}{3}}=75\]cm/s
|
|
Câu 8: Một vật dao động điều hòa với phương trình \[x=A\cos \left( 4\pi t \right)cm\], khoảng thời gian ngắn nhất kể từ lúc bắt đầu dao động đến lúc vật có li độ \[x=-0,5A\]là
A. \[\frac{1}{3}\] s B. \[\frac{1}{12}\] s D. \[\frac{1}{6}\] s D. \[\frac{1}{8}\] s
Hướng dẫn
|
+ Thời điểm ban đầu \[t=0\Rightarrow x=A\] + Thời gian ngăn nhất vật đến vị trí \[x=-\frac{A}{2}\], ứng với góc quét \[\Delta \varphi =\frac{\pi }{2}+\frac{\pi }{6}=\frac{2\pi }{3}ra\text{d}\Rightarrow t=\frac{\Delta \varphi }{\omega }=\frac{\frac{2\pi }{3}}{4\pi }=\frac{1}{6}s\]
|
|
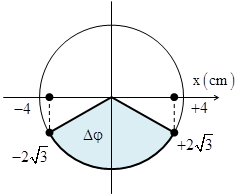
Câu 9: Một vật dao động điều hòa với phương trình \[x=4\cos \left( 8\pi t-\frac{\pi }{6} \right)cm\], khoảng thời gian ngắn nhất vật đi từ li độ \[x=-2\sqrt{3}cm\] theo chiều dương đến li độ \[x=2\sqrt{3}cm\] theo chiều dương là
A. \[\frac{1}{6}\] s B. \[\frac{1}{12}\] s D. \[\frac{1}{10}\] s D. \[\frac{1}{20}\] s
Hướng dẫn
|
+ Vật chuyển động theo chiều dương tương ứng với chuyển động của vật ở nửa đường tròn dưới. + Từ hình vẽ ta có: \[\Delta \varphi =\frac{2\pi }{3}ra\text{d}\] \[\Rightarrow t=\frac{\Delta \varphi }{\omega }=\frac{1}{12}s\]
|
|
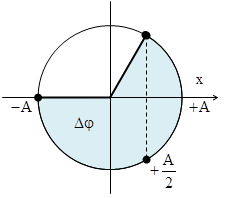
Câu 10: Một con lắc lò xo dao động điều hòa với biên độ A. Trong một chu kì thời gian dài nhất để con lắc di chuyển từ vị trí có li độ \[{{x}_{1}}=-A\] đến vị trí có li độ \[{{x}_{2}}=\frac{A}{2}\] là 1 s. Chu kì dao động của vật là
A. 1,4 s B. 2 s D. 3 s D. 4 s
Hướng dẫn
|
+ Thời gian dài nhất ứng với chuyển động của vật từ vị trí biên âm đến vị trí \[x=\frac{A}{2}\] theo chiều dương + Từ hình vẽ ta thấy rằng \[t=\frac{\Delta \varphi }{\omega }\Leftrightarrow 1=\frac{\pi +\frac{\pi }{3}}{\omega }\Rightarrow \omega =\frac{4\pi }{3}\]rad/s + Chu kì dao động của vật \[T=\frac{2\pi }{\omega }=1,5\text{s}\]
|
|
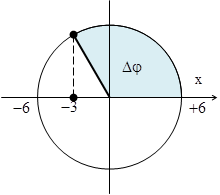
Câu 11: Một vật dao động điều hòa trên quỹ đạo dài 8 cm. Sau 0,25 s kể từ thời điểm ban đầu vật đi được 4 cm mà chưa đổi chiều chuyển động và vật đến vị trí có li độ 2 cm. Tần số dao động của vật là
A. \[\frac{2}{3}\]Hz B. 0,75 Hz D. 1,5 Hz D. \[\frac{4}{2}Hz\]
Hướng dẫn
|
+ Biên độ dao động của vật \[A=\frac{L}{2}=4cm\] + Từ hình vẽ, ta thấy rằng \[t=\frac{\Delta \varphi }{\omega }\Leftrightarrow 0,25=\frac{\frac{\pi }{6}+\frac{\pi }{6}}{\omega }\Rightarrow \omega =\frac{4\pi }{3}\]rad/s + Tần số của dao động \[f=\frac{\omega }{2\pi }=\frac{2}{3}H\text{z}\]
|
|
Câu 12: Một vật dao động điều hòa với chu kì 2 s. Trong quá trình dao động vận tốc của vật có độ lớn cực đại là 6π cm/s, lấy π2 = 10. Thời gian ngắn nhất để vật đi từ vị trí \[x=6\]cm đến \[x=-3\sqrt{3}\]cm là
A. 0,833 s B. 0,167 s D. 0,333 s D. 0,667 s
Hướng dẫn
|
+ Tần số góc của dao động \[\omega =\frac{2\pi }{T}=\pi \]rad/s + Biên độ dao động của vật \[{{v}_{max}}=\omega A\Rightarrow A=\frac{{{v}_{max}}}{\omega }=6cm\] + Từ hình vẽ, ta có:\[t=\frac{\Delta \varphi }{\omega }=\frac{\frac{\pi }{2}+\frac{\pi }{3}}{\pi }=\frac{5}{6}s\]
|
|
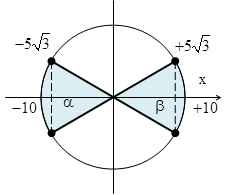
Câu 13: Một con lắc lò xo đang dao động điều hòa với biên độ 10 cm, chu kì 1 s. Trong một chu kì, khoảng thời gian mà khoảng cách từ vật đến vị trí cân bằng lớn hơn hoặc bằng giá trị \[5\sqrt{3}\]cm là
A. \[\frac{1}{3}\]s B. \[\frac{1}{12}\] s D. \[\frac{5}{12}\] s D. \[\frac{1}{6}\]s
Hướng dẫn
|
+ Khoảng cách từ vật đến vị trí cân bằng \[d=\left| x \right|\ge 5\sqrt{2}cm\] + Từ hình vẽ, khoảng thời gian tương ứng với góc quét \[\Delta \varphi =\alpha +\beta =\frac{\pi }{3}+\frac{\pi }{3}=\frac{2\pi }{3}ra\text{d}\] + Thời gian cần tìm \[t=\frac{\Delta \varphi }{\omega }=\frac{1}{3}s\]
|
|
Câu 14: Một vật nhỏ dao động điều hòa theo phương trình \[x=6\cos \left( 4\pi t \right)\]cm (t được tính bằng s). Từ thời điểm t = 0, khoảng thời gian ngắn nhất để gia tốc của vật bằng một nửa gia tốc cực đại là
A. 0,083 s B. 0,104 s D. 0,167 s D. 0,125s
Hướng dẫn
|
+ Tại thời điểm \[t=0\Rightarrow x=6cm\] + Ta có \[a=-{{\omega }^{2}}x=\frac{1}{2}{{\omega }^{2}}A\Rightarrow x=-\frac{A}{2}\] + Từ hình vẽ, ta xác định được khoảng thời gian tương ứng là \[t=\frac{\Delta \varphi }{\omega }=\frac{\frac{\pi }{2}+\frac{\pi }{6}}{4\pi }=\frac{1}{6}s\]
|
|
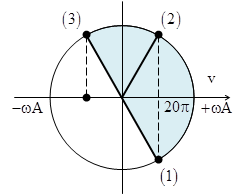
Câu 15: Một vật đang dao động điều hòa, gọi t1, t2 và t3 lần lượt là ba thời điểm liên tiếp vật có cùng tốc độ. Biết rằng \[{{t}_{3}}-{{t}_{1}}=3\left( {{t}_{3}}-{{t}_{2}} \right)=0,1s\] và \[{{v}_{1}}={{v}_{2}}=-{{v}_{3}}=20\pi \]cm/s. Tính biên độ dao động của vật
A. 4 cm B. 5 cm D. 3 cm D. 2 cm
Hướng dẫn
|
+ Ta để ý rằng hai thời điểm t1 và t3 vận tốc trái dấu nhau\[\Rightarrow \] hai vị trí này đối xứng với nhau qua gốc tọa độ \[\Rightarrow {{\varphi }_{13}}=\pi a\text{d}\] + Mặc khác \[{{t}_{3}}-{{t}_{1}}=3\left( {{t}_{3}}-{{t}_{2}} \right)\Rightarrow {{\varphi }_{13}}=3{{\varphi }_{32}}\Rightarrow {{\varphi }_{32}}=\frac{\pi }{6}\] + Từ hình vẽ, ra có: \[\sin \frac{{{\varphi }_{32}}}{2}=\frac{10\pi }{\omega A}\Rightarrow \omega A=20\pi \]cm/s + Kết hợp với \[{{t}_{13}}=\frac{{{\varphi }_{13}}}{\omega }=0,1\text{s}\Leftrightarrow \omega =10\pi \]rad/s Thay vào phương trình trên ta tìm được \[A=2cm\]
|
|
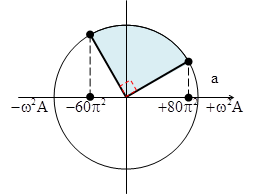
Câu 16: Một vật dao động điều hòa với chu kì T và biên độ A = 4 cm. Biết rằng trong một chu kì, khoảng thời gian để gia tốc của vật thõa mãn \[-60{{\pi }^{2}}\le a\le 80{{\pi }^{2}}cm.{{s}^{-2}}\]là \[\frac{T}{2}\]. Chu kì dao động của con lắc là
A. 0,3 s B. 0,4 s D. 0,5 s D. 0,6 s
Hướng dẫn
|
+ Ta để ý rằng hai thời điẻm liên tiếp gia tốc biến đổi từ \[-60{{\pi }^{2}}\]cm/s2 đến 80π2 cm/s2 vuông pha nhau + Vâyu gia tốc cực đại của vật là \[{{a}_{ma\text{x}}}={{\omega }^{2}}A=\sqrt{{{\left( -60{{\pi }^{2}} \right)}^{2}}+{{\left( 80{{\pi }^{2}} \right)}^{2}}}=100{{\pi }^{2}}\] cm/s2 + Từ đây tà tìm được \[\omega =\sqrt{\frac{100{{\pi }^{2}}}{4}}=5\pi \Rightarrow T=0,4\text{s}\]
|
|
Câu 17: Một vật dao động điều hòa với với phương trình \[x=4\cos \left( \omega t-\frac{\pi }{3} \right)\]cm. Trong một chu kì dao động, khoảng thời gian mà gia tốc của vật có độ lớn lớn hơn \[0,5{{a}_{max}}\] là 0,4 s. Khoảng thời gian ngắn nhất kể từ khi vật dao động đến khi vật qua vị trí có tốc độ bằng \[0,5{{v}_{max}}\]lần thứ hai là
A. 0,15 s B. 0,4 s D. 0,5 s D. 0,8 s
Hướng dẫn
|
+ Khoảng thời gian gia tốc của vật có độ lớn lớn hơn \[\frac{{{a}_{ma\text{x}}}}{2}\] ứng với \[t=\frac{2T}{3}=0,4\Rightarrow T=0,6\text{s}\]+ Ban đầu vật đi qua vị trí có li độ \[x=2cm\] theo chiều dương \[\Rightarrow \]khoảng thời gian cần tìm là\[t=\frac{T}{4}=0,15\text{s}\]
|
|
Câu 18: Một vật dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều điểm O. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó khi đi qua các điểm M, N là 20π cm/s. Biên độ A của dao động là
A. 4 cm B. 6 cm D. \[4\sqrt{2}\]cm D. \[4\sqrt{3}\]cm
Hướng dẫn
|
+ Cứ sau 0,05 s chất điểm lại đi qua các điểm M, O và N \[\Rightarrow {{\varphi }_{MO}}={{\varphi }_{ON}}={{\varphi }_{NM}}\] + Từ hình vẽ, ta thấy rằng \[{{\varphi }_{ON}}=\frac{\pi }{3}\Rightarrow T=6.0,05=0,3\text{s}\] Tại các vị trí M và N, ta có \[\left| v \right|=\frac{{{v}_{ma\text{x}}}}{a}\Rightarrow {{v}_{max}}=40\pi \Rightarrow A=6cm\]
|
|
Câu 19: Một vật con lắc lò xo dao động điều hòa với phương trình \[x=A\cos \left( \omega t+\varphi \right)\]cm. Tại thời điểm t1, vật có vận tốc \[{{v}_{1}}=50\]cm/s, gia tốc \[a=-10\sqrt{3}\]m/s2. Tại thời điểm \[{{t}_{2}}={{t}_{1}}+\Delta t\left( \Delta t>0 \right)\], vật có vận tốc là \[{{v}_{2}}=-50\sqrt{2}\]cm/s, gia tốc \[a=10\sqrt{2}\]m/s2. Giá trị nhỏ nhất của Δt
A. \[\frac{11\pi }{240}s\] B. \[\frac{13\pi }{240}s\] D. \[\frac{9\pi }{240}s\] D. \[\frac{17\pi }{240}s\]
Hướng dẫn
|
+ Với hai đại lượng vuông pha a và v, ta có phương trình độc lập \[{{\left( \frac{v}{{{v}_{ma\text{x}}}} \right)}^{2}}+{{\left( \frac{a}{{{a}_{ma\text{x}}}} \right)}^{2}}=1\] + Với hai thời điểm t1 và t2 ta có hệ
+ Từ hình vẽ, ta xác định được khoảng thời gian tương ứng là \[t=\frac{\Delta \varphi }{\omega }=\frac{\frac{\pi }{6}+\frac{\pi }{2}+\frac{\pi }{4}}{20}=\frac{11\pi }{240}s\]
|
|