PP Đường Tròn Trong Dao Động Điều Hòa

PHƯƠNG PHÁP ĐƯỜNG TRÒN TRONG GIAO ĐỘNG ĐIỀU HÒA

 

I. CƠ SỞ LÝ THUYẾT – MỐI LIÊN HỆ GIỮA DAO ĐỘNG CƠ VÀ CHUYỂN ĐỘNG TRÒN ĐỀU

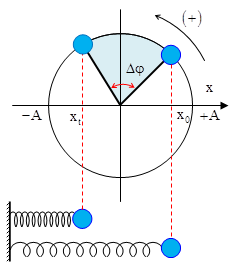
Dao động điều hòa được xem là hình chiếu của một vật chuyển động tròn với bán kính \[R=A\] và tốc độ dài \[v=r\omega \] Các bước thực hiện Bước 1: Vẽ đường tròn tâm O bán kính \[R=A\] Bước 2: Xác định vị trí tương ứng của vật trên đường tròn tại thời điểm t0 và thời điểm t + Vật chuyển động theo chiều dương (\[{{\varphi }_{0}}<0\]) tương ứng với vị trí ở nửa dưới đường tròn + Vật chuyển động theo chiều âm (\[{{\varphi }_{0}}>0\]) tương ứng với vị trí ở nửa trên đường tròn Bước 3: Xác định góc quét Δφ tương ứng giữa hai thời điểm Áp dụng \[t=\frac{\Delta \varphi }{\omega }\]

 

II. CÁC BÀI TOÁN LIÊN QUAN:

1. Bài toán xác định thời gian ngắn nhất vật đi giữa hai vị trí

Hướng dẫn:

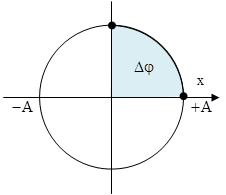
+ Vị trí gia tốc có độ lớn cực đại ứng với \[x=A\] + Vị trí vận tốc cực đại ứng với \[x=0\] + Góc quét tương ứng \[\Delta \varphi =\frac{\pi }{2}\] Thời gian tương ứng với góc quét này \[t=\frac{\Delta \varphi }{\omega }=\frac{\frac{\pi }{2}}{\frac{2\pi }{T}}=\frac{T}{4}\] Đáp án C

2. Bài toán xác định thời điểm vật đi qua vị trí có li độ x₀

Hướng dẫn:

Chu kì của dao động \[T=\frac{2\pi }{\omega }=\frac{2\pi }{\frac{2\pi }{3}}=3\]s Trong mỗi chu kì, vật sẽ đi qua vị trí \[x=-2cm\]hai lần\[\Rightarrow \]cần 1008 chu kì để vật đi qua vị trí này Từ hình vẽ, ta có khoảng thời gian để vật đi qua vị trí \[x=-2cm\] lần đầu tiên kể từ thời điểm ban đầu là\[\Delta t=\frac{\varphi }{\omega }=1s\] Vậy thời gian để vật đi qua vị trí \[x=-2cm\] lần thứ 2017 kể từ thời điểm ban đầu là \[t=100T+\Delta t=3035\text{s}\]

• Đáp án D

3. Bài toán liên quan đến thời gian li độ, vận tốc, gia tốc lớn hơn hoặc nhỏ hơn một giá trị cho trướng

Hướng dẫn:

Gia tốc cực đại của con lắc \[{{a}_{\max }}={{\omega }^{2}}A\] Để gia tốc có độ lớn không vượt quá 100 cm/s2 ứng với khoảng thời gian \[t=\frac{T}{3}\] \[\Rightarrow 4\varphi =\frac{4\pi }{3}\Leftrightarrow \varphi =\frac{\pi }{3}\] Mặc khác \[\cos \varphi =\frac{100}{{{\omega }^{2}}A}\Rightarrow \omega =\sqrt{\frac{100}{A\cos \varphi }}=2\pi \]rad/s Tần số của dao động \[f=\frac{\omega }{2\pi }=1Hz\]

• Đáp án D

4. Bài toán liên quan đến quãng đường, tốc độ trung bình trong dao động điều hòa

Hướng dẫn:

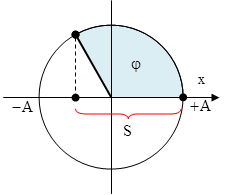
Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ \[x=A\] đến vị trí \[x=-\frac{A}{2}\]ứng với góc quét φ. Từ hình vẽ ta tính được \[\varphi =\frac{\pi }{2}+\frac{\pi }{6}=\frac{2\pi }{3}\Rightarrow t=\frac{T}{3}\] Quãng đường S tương ứng mà vật đi được trong khoảng thời gian này là \[S=A+\frac{A}{2}=\frac{3}{2}A\] \[\Rightarrow \]tốc độ trung bình của chất điểm này \[{{v}_{tb}}=\frac{S}{t}=\frac{9A}{2T}\]

• Đáp án B

 

Hướng dẫn:

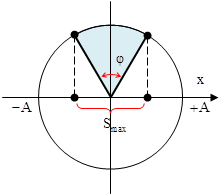
Vật đi được quãng đường lớn nhất khi nó chuyển động ở những vị trí gần vị trí cân bằng nhất

+ Góc quét φ ứng với khoảng thời gian Δt: \[\varphi =\omega \Delta t\]

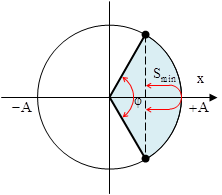
+ Quãng đường lớn nhất vật đi được:\[{{S}_{m\text{ax}}}=2A\sin \left( \frac{\varphi }{2} \right)=2A\sin \left( \frac{\omega \Delta t}{2} \right)\]

Vật đi được quãng đường nhỏ nhất khi nó chuyển động ở những vị trí xa vị trí cân bằng nhất

+ Quãng đường nhỏ nhất mà vật đi được:\[{{S}_{\min }}=2A\left[ 1-\cos \left( \frac{\varphi }{2} \right) \right]=2A\left[ 1-\cos \left( \frac{\varphi }{2} \right) \right]\]

• Đáp án A

 

5. Vòng tròn đa trục để xác định tính chất của chuyển động, các đại lượng liên quan

Hướng dẫn:

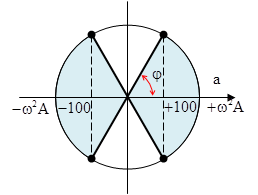
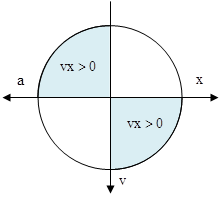
Sử dụng vòng tròn đa trục + Trục Ox nằm ngang, chiều dương từ trái sang phải + Trục Oa nằm ngang, chiều dương từ phải sang trái + Trục Ov thẳng đứng, chiều dương hướng xuống dưới Từ hình vẽ, ta có khoảng thời gian tương ứng là\[t=\frac{T}{2}\]

• Đáp án A

 

III. BÀI TậP VẬN DỤNG

Câu 1: Một vật dao động điều hòa trên một quỹ đạo có chiều dài 10 cm. Quãng đường mà vật này đi được trong một chu kì là:

          A. 10 cm                      B. 15 cm                      C. 20 cm      D. 25 cm

Câu 2: Một con lắc lò xo đang dao động điều hòa theo phương ngang. Khi vật đi qua vị trí cân bằng tốc độ của vật nặng là 4π cm/s, gia tốc cực đại mà vật nặng đạt được là 40 cm/s². Quãng đường mà vật này đi được trong khoảng thời gian \[\frac{T}{2}\] là:

          A. 4 cm                        B. 8 cm                        C. 16 cm      D. 32 cm

Câu 3: Trong dao động điều hòa. Thời gian để một chất điểm đi từ vị trí \[x=+A\] đến vị trí có li độ \[x=0\]lần thứ 2 sẽ là:

          A. T                             B. \[\frac{T}{2}\]        C. \[\frac{3T}{4}\]                     D. \[\frac{T}{4}\]

Câu 4: Một vật nhỏ dao động điều hòa theo phương trình \[x=A\cos \left( 4\pi t \right)\]cm (t tính bằng s). Tính từ thời điểm \[t=0\] thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại

          A. 0,083 s                    B. 0,104 s                     C. 0,167 s         D. 0,125 s

Câu 5: Một vật nhỏ dao động điều hòa theo quỹ đạo thẳng dài 14 cm với chu kì 1 s. Từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến thời điểm gia tốc của vật đạt giá trị cực tiểu lần thứ 2. Vật có tốc độ trung bình là:

          A. 27,3 cm/s                 B. 28,0 cm/s                 C. 27,0 cm/s   D. 26,7 cm/s

Câu 6: Một vật dao động điều hòa với chu kì T. Biết rằng khoảng thời gian giữa hai lần liên tiếp động  năng của vật bằng thế năng là 1 s. Chu kì của dao động:

          A. 1 s                           B. 2 s                           C. 3 s         D. 4 s

Câu 7: Một vật dao động điều hòa theo phương trình \[x=4\cos \left( 2\pi t \right)\]cm (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí động năng bằng thế năng đến vị trí động năng bằng 3 lần thế năng là:

          A. \[\frac{1}{12}\]s     B. \[\frac{1}{24}\]s      C. \[\frac{1}{6}\]s                      D. \[\frac{1}{3}\]s

Câu 8: Phương trình li độ của một chất điểm dao động điều hòa được cho bởi \[x=2\cos \left( \pi t \right)\]cm (t tính bằng s). Tốc độ trung bình của chất điểm kể từ thời điểm ban đầu đến khi nó đi qua vị trí có động năng bằng 3 lần thế năng lần thứ nhất.

          A. 3 cm/s                     B. 4 cm/s                      C. 5 cm/s   D. 6 cm/s

Câu 9: Chọn phát biểu sai. Trong dao động điều hòa

          A. quãng đường vật đi được trong một chu kì là 4A

          B. quãng đường mà vật đi được trong khoảng thời gian \[\frac{T}{2}\] là 2A

          C. quãng đường vật đi được trong \[\frac{T}{4}\] là A

          D. quãng đường mà vật đi được trong khoảng thời gian 2T là 8A

Câu 10 : Trong dao động điều hòa của một vật. Khoảng thời gian trong một chu kì để vận tốc của vật có độ lớn  \[\left| v \right|\le 0,5{{v}_{m\text{ax}}}\]là :

          A. \[\frac{T}{3}\]        B. \[\frac{T}{4}\]        C. \[\frac{T}{5}\]                       D. \[\frac{T}{6}\]

Câu 11 : Xác định thời gian để vật đi qua vị trí gia tốc cực tiểu lần thứ 2 kể từ thời điểm ban đầu. Biết rằng ban đầu vật đang ở vị trí biên âm và vật dao động với chu kì 4s.

          A. 5 s                           B. 6 s                           C. 10 s         D. 12 s

Câu 12 : Một vật dao động điều hòa với biên độ A và tần số góc π rad/s. Thời gian ngắn nhất trong một chu kì để hai lần liên tiếp vật đi qua vị trí có động năng bằng 3 lần thế năng :

          A. \[\frac{2}{3}\] s      B. \[\frac{1}{3}\] s      C. 1 s         D. 2 s

Câu 13 : Biết rằng trong một chu kì quãng đường mà vật dao động điều hòa đi được là 20 cm, tần số góc của dao động là π rad/s. Thời gian để vật từ vị trí biên âm đi qua vị trí vật có vận tốc 5π rad/s lần đầu tiên là :

          A. 1 s                           B. 2 s                           C. 0,5 s         D. 0,25 s

Câu 14 : Phương trình li độ của một vật dao động điều hòa được cho bởi \[x=4\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm (t tính bằng s). Quãng đường mà vật đi được từ thời điểm ban đầu đến vị trí mà gia tốc của vật bằng một nửa gia tốc cực đại lần đầu tiên

          A. 4 cm                        B. 2 cm                        C. 8 cm      D. 16 cm

Câu 15 : Một vật dao động điều hòa theo phương trình \[x=5\cos \left( \pi t+\frac{\pi }{2} \right)\]cm (t được tính bằng s). Quãng đường lớn nhất mà vật đi được trong \[\frac{2}{3}\] s là :

          A. 5 cm                        B. \[5\sqrt{2}\]cm        C. \[5\sqrt{3}\]cm                       D. 6 cm

Câu 16 : Một con lắc gồm lò xo có độ cứng 100 N/m, vật nặng có khối lượng 100 g dao động điều hòa với biên độ 4 cm. Tốc độ trung bình của vật khi nó đị từ vị trí biên dương đến vị trí động năng bằng 3 lần thế năng lần thứ 2 là :

          A. 75 cm/s                    B. 80 cm/s                    D. 90 cm/s   D. 100 cm/s

Câu 17 : Một vật dao động điều hòa với phương trình \[x=A\cos \left( 4\pi t \right)cm\], khoảng thời gian ngắn nhất kể từ lúc bắt đầu dao động đến lúc vật có li độ \[x=-0,5A\]là

          A. \[\frac{1}{3}\] s      B. \[\frac{1}{12}\] s     D. \[\frac{1}{6}\] s                     D. \[\frac{1}{8}\] s

Câu 18 : Một vật dao động điều hòa với phương trình \[x=4\cos \left( 8\pi t-\frac{\pi }{6} \right)cm\], khoảng thời gian ngắn nhất vật đi từ li độ \[x=-2\sqrt{3}cm\] theo chiều dương đến li độ \[x=2\sqrt{3}cm\] theo chiều dương là

          A. \[\frac{1}{6}\] s      B. \[\frac{1}{12}\] s     D. \[\frac{1}{10}\] s                   D. \[\frac{1}{20}\] s

Câu 19: Một con lắc lò xo dao động điều hòa với biên độ A. Trong một chu kì thời gian dài nhất để con lắc di chuyển từ vị trí có li độ \[{{x}_{1}}=-A\] đến vị trí có li độ \[{{x}_{2}}=\frac{A}{2}\] là 1 s. Chu kì dao động của vật là

          A. 1,4 s                        B. 2 s                           D. 3 s         D. 4 s

Câu 20: Một vật dao động điều hòa trên quỹ đạo dài 8 cm. Sau 0,25 s kể từ thời điểm ban đầu vật đi được 4 cm mà chưa đổi chiều chuyển động và vật đến vị trí có li độ 2 cm. Tần số dao động của vật là

          A. \[\frac{2}{3}\]Hz    B. 0,75 Hz                   D. 1,5 Hz      D. \[\frac{4}{2}Hz\]

Câu 21: Một vật dao động điều hòa với chu kì 2 s. Trong quá trình dao động vận tốc của vật có độ lớn cực đại là 6π cm/s, lấy π² = 10. Thời gian ngắn nhất để vật đi từ vị trí \[x=6\]cm đến \[x=-3\sqrt{3}\]cm là

          A. 0,833 s                    B. 0,167 s                     D. 0,333 s         D. 0,667 s

Câu 22: Một con lắc lò xo đang dao động điều hòa với biên độ 10 cm, chu kì 1 s. Trong một chu kì, khoảng thời gian mà khoảng cách từ vật đến vị trí cân bằng lớn hơn hoặc bằng giá trị \[5\sqrt{3}\]cm là

          A. \[\frac{1}{3}\]s       B. \[\frac{1}{12}\] s     D. \[\frac{5}{12}\] s                   D. \[\frac{1}{6}\]s

Câu 23: Một vật nhỏ dao động điều hòa theo phương trình \[x=6\cos \left( 4\pi t \right)\]cm (t được tính bằng s). Từ thời điểm t = 0, khoảng thời gian ngắn nhất để gia tốc của vật bằng một nửa gia tốc cực đại là

          A. 0,083 s                    B. 0,104 s                     D. 0,167 s         D. 0,125s

Câu 24: Một vật đang dao động điều hòa, gọi t₁, t₂ và t₃ lần lượt là ba thời điểm liên tiếp vật có cùng tốc độ. Biết rằng \[{{t}_{3}}-{{t}_{1}}=3\left( {{t}_{3}}-{{t}_{2}} \right)=0,1s\] và \[{{v}_{1}}={{v}_{2}}=-{{v}_{3}}=20\pi \]cm/s. Tính biên độ dao động của vật

          A. 4 cm                        B. 5 cm                        D. 3 cm      D. 2 cm

Câu 25: Một vật dao động điều hòa với chu kì T và biên độ A = 4 cm. Biết rằng trong một chu kì, khoảng thời gian để gia tốc của vật thõa mãn \[-60{{\pi }^{2}}\le a\le 80{{\pi }^{2}}cm.{{s}^{-2}}\]là \[\frac{T}{2}\]. Chu kì dao động của con lắc là

          A. 0,3 s                        B. 0,4 s                        D. 0,5 s         D. 0,6 s

Câu 26: Một vật dao động điều hòa với với phương trình \[x=4\cos \left( \omega t-\frac{\pi }{3} \right)\]cm. Trong một chu kì dao động, khoảng thời gian mà gia tốc của vật có độ lớn lớn hơn \[0,5{{a}_{max}}\] là 0,4 s. Khoảng thời gian ngắn nhất kể từ khi vật dao động đến khi vật qua vị trí có tốc độ bằng \[0,5{{v}_{max}}\]lần thứ hai là

          A. 0,15 s                      B. 0,4 s                        D. 0,5 s         D. 0,8 s

Câu 27: Một vật dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều điểm O. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó khi đi qua các điểm M, N là 20π cm/s. Biên độ A của dao động là

          A. 4 cm                        B. 6 cm                        D. \[4\sqrt{2}\]cm                       D. \[4\sqrt{3}\]cm

Câu 28: Một vật con lắc lò xo dao động điều hòa với phương trình \[x=A\cos \left( \omega t+\varphi  \right)\]cm. Tại thời điểm t₁, vật có vận tốc \[{{v}_{1}}=50\]cm/s, gia tốc \[a=-10\sqrt{3}\]m/s². Tại thời điểm \[{{t}_{2}}={{t}_{1}}+\Delta t\left( \Delta t>0 \right)\], vật có vận tốc là \[{{v}_{2}}=-50\sqrt{2}\]cm/s, gia tốc \[a=10\sqrt{2}\]m/s². Giá trị nhỏ nhất của Δt

          A. \[\frac{11\pi }{240}s\]                                 B. \[\frac{13\pi }{240}s\]            D. \[\frac{9\pi }{240}s\]                                D. \[\frac{17\pi }{240}s\]

 

ĐÁP ÁN

1.C	2.B	3.C	4.C	5.C	6.D	7.B	8.D	9.C	10.A
11.B	12.B	13.C	14.A	15.C	16.C	17.C	18.B	19.A	20.A
21.A	22.A	23.C	24.D	25.B	26.A	27.B	28.A

 

Bài viết gợi ý: