Một trong những chương trình sách giáo khoa toán lớp 8 cơ bản nhất mà bạn cần biết chính là phần Đa diện, diện tích đa thức cơ bản với cách giải đơn giản nhất.
Theo đó, bạn cần nắm được kiến thức cơ bản nhất của phần này để có thể hoàn thành kỳ thi cuối kỳ cũng như chuẩn bị kiến thức lên lớp 9 cơ bản nhất. Dưới đây là một số bài toán mà bạn cần nhớ:
Bài 1: Hãy vẽ phác một lục giác lồi.
Hãy nêu cách nhận biết một đa giác lồi.
Lời giải:
- Lục giác lồi ABCDEF
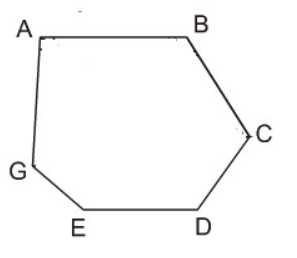
- Cách nhận biết một đa giác lồi: Một đa giác lồi là một đa giác thỏa mãn điều kiện sau:
+ Các cạnh chỉ cắt nhau tại các đỉnh, nghĩa là không có hai cạnh nào cắt nhau tại một điểm mà không phải là đỉnh. Một đa giác thỏa mãn điều kiện này là đa giác đơn.
+ Đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa một cạnh tùy ý của nó. Một đa giác đơn thỏa mãn thêm điều kiện này là một đa giác lồi.
Bài 2: Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:
a) Có tất cả các cạnh bằng nhau.
b) Có tất cả các góc bằng nhau.
Lời giải:
a) Hình thoi có tất cả các cạnh bằng nhau nhưng các góc có thể không bằng nhau nên hình thoi không buộc phải là đa giác đều.
b) Hình chữ nhật có tất cả các góc bằng nhau nhưng các cạnh có thể không bằng nhau nên hình chữ nhật không buộc phải là đa giác đều.
Bài 3: Cho hình thoi ABCD có góc ∠A = 60o. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
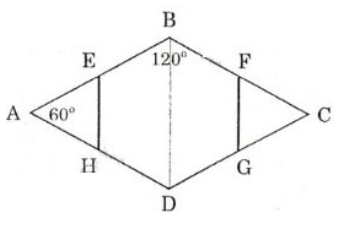
Lời giải:
ABCD là hình thoi, \[\widehat{A}={{60}^{0}}\] nên \[\widehat{B}=\widehat{D}={{120}^{0}}\]
\[\vartriangle EAH\] là tam giác đều( vì tam giác cân có một góc 600 nên \[\widehat{BEH}={{120}^{0}},\widehat{DHE}={{120}^{0}}\])
Tương tự \[\widehat{BFG}={{120}^{0}},\widehat{FGD}={{120}^{0}}\]
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau (bằng nửa cạnh hình thoi).
Vậy EBFGDH là một lục giác đều.
Bài 5: Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.
Lời giải:
Tổng số đo các góc cảu hình n giác bằng \[(n-2){{.180}^{0}}\]
Suy ra số đo mỗi góc của hình n giác đều là \[\frac{(n-2){{.180}^{0}}}{n}\]
Áp dụng công thức trên, ta có:
- Số đo mỗi góc của ngũ giác đều là \[\frac{(5-2){{.180}^{0}}}{5}={{108}^{0}}\]
- Số đo mỗi góc của lục giác đều là \[\frac{(6-2){{.180}^{0}}}{6}={{120}^{0}}\]







