Một trong những kiến thức cơ bản nhất của chương trình toán lớp 8 nhất trong chương trình sách giáo khoa mà bạn cần nhớ là Tam giác đồng dạng với cách giải đơn giản nhất.
Sau đây là một số bài toán đơn giản nhất mà bạn có thể tham khảo:
Bài 1: Viết tỉ số của hai đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD = 15 cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
Bài giải.
a) AB = 5cm và CD = 15 cm
\[\Leftrightarrow \]\[\frac{AB}{CD}=\frac{5}{15}=\frac{1}{3}\]
b) EF = 48cm và GH = 16dm
\[\Leftrightarrow \]\[\frac{FE}{GH}=\frac{48}{160}=\frac{3}{10}\]
c) PQ = 1,2m và MN = 24cm
\[\Leftrightarrow \]\[\frac{PQ}{MN}=\frac{120}{24}=5\]
Bài 2 Cho biết \[\frac{AB}{CD}=\frac{3}{4}\] và CD bằng 12cm. Tính độ dài của AB.
Giải.
Thay CD = 12cm vào tỉ số độ dài ta được:
\[\frac{AB}{12}=\frac{3}{4}\Rightarrow AB=\frac{12.3}{4}=9.\]
Vậy độ dài AB = 9cm
Bài 3 Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.
Giải.
Độ dài AB gấp 5 lần độ dài của CD nên AB = 5CD.
Độ dài A'B' gấp 12 lần độ dài của CD nên A'B' = 12CD.
=> Tỉ số của hai đoạn thẳng AB và A'B' là: \[\frac{AB}{A'B'}=\frac{5CD}{12CD}=\frac{5}{12}\]
Bài 4: Cho biết \[\frac{AB'}{AB}=\frac{AC'}{AC}\] (h.6). Chứng minh rằng:
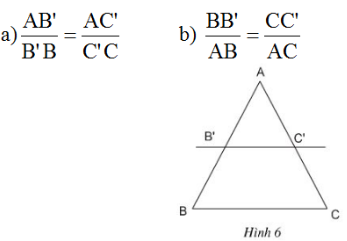
Giải.

Bài 5 Tính x trong các trường hợp sau (h.7):
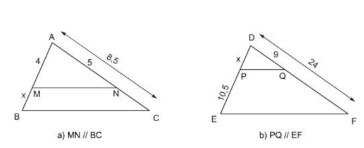
Giải.








