Bài 4. Cô giáo yêu cầu mỗi bạn cho một ví dụ về hai phân thức đại số bằng nhau. Dưới đây là những ví dụ các bạn Lan, Hùng, Hương, Huy đã cho:
a) \[\frac{x+3}{2x-5}=\frac{{{x}^{2}}+3x}{2{{x}^{2}}-5x}\] ( Lan); b) \[\frac{{{(x+1)}^{2}}}{{{x}^{2}}+x}=\frac{x+1}{1}\]
c) \[\frac{4-x}{-3x}=\frac{x-4}{3x}\] ( Giang); d) \[\frac{{{(x-9)}^{3}}}{2(9-x)}=\frac{{{(9-x)}^{2}}}{2}\] ( Huy)
Giải.
a) \[\frac{x+3}{2x-5}=\frac{x(x+3)}{(2x-5)x}=\frac{{{x}^{2}}+3x}{2{{x}^{2}}-5x}\] Lan viết đúng
b) \[\frac{{{(x+1)}^{2}}}{{{x}^{2}}+x}=\frac{{{(x+1)}^{2}}}{x(x+1)}=\frac{x+1}{x}\] Hùng viết sai vì đã chia tử của vế trái cho nhân tử chung \[x+1\] thì cũng phải chia mẫu của nó cho \[x+1\]. Sửa lại là:
\[\frac{{{(x+1)}^{2}}}{{{x}^{2}}+x}=\frac{x+1}{x}\] hoặc \[\frac{{{(x+1)}^{2}}}{x+1}=\frac{x+1}{1}\]
c) \[\frac{4-x}{-3x}=\frac{-(4-x)}{-(-3x)}=\frac{x-4}{3x}\] Giang viết đúng
d) \[{{(x9)}^{3}}={{(-(9x))}^{3}}=-{{(9x)}^{3}}\] nên \[\frac{{{(x-9)}^{3}}}{2(9-x)}=\frac{-{{(9-x)}^{3}}}{2(9-x)}=\frac{-{{(9-x)}^{2}}}{2}\]
Sửa lại: \[\frac{{{(x-9)}^{3}}}{2(9-x)}=\frac{-{{(9-x)}^{2}}}{2}\] hoặc \[\frac{{{(x-9)}^{3}}}{2(9-x)}=\frac{{{(9-x)}^{2}}}{-2}\] hoặc \[\frac{{{(9-x)}^{3}}}{2(9-x)}=\frac{{{(9-x)}^{2}}}{2}\]
Bài 5. Điền đa thức thích hợp vào mỗi chỗ trống trong các đẳng thức sau:
a) \[\frac{{{x}^{3}}+{{x}^{2}}}{(x-1)(x+1)}=\frac{...}{x-1}\]
b) \[\frac{5(x+y)}{2}=\frac{5{{x}^{2}}-5{{y}^{2}}}{...}\]
Giải.
a) \[\frac{{{x}^{3}}+{{x}^{2}}}{{{x}^{2}}-1}=\frac{{{x}^{2}}(x+1)}{(x-1)(x+1)}=\frac{{{x}^{2}}}{x-1}\]
Vậy phải điền \[{{x}^{2}}\] vào chỗ trống
b) \[\frac{5\left( x+y \right)}{2}=\frac{5\left( x+y \right)\left( x-y \right)}{2\left( x-y \right)}=\frac{5\left( {{x}^{2}}-{{y}^{2}} \right)}{2\left( x-y \right)}\]
Vậy phải điền \[2x-2y\]vào chỗ trống.
Bài 6. Đố. Hãy dùng tính chất cơ bản của phân thức để điền một đa thức thích hợp vào chỗ trống:
\[\frac{{{x}^{5}}-1}{{{x}^{2}}-1}=\frac{...}{x+1}\]
Giải.
Ta có: \[{{x}^{2}}-1=(x-1)(x+1)\]
Vế phải chứng tỏ đã chia mẫu của vế trái cho \[x-1\]
Vậy phải chia tử của vế trái \[{{x}^{5}}1\] cho \[x-1\]
Vậy phải điền vào chỗ trống : \[{{x}^{4}}+{{x}^{3}}+{{x}^{2}}+x+1\]
Bài 1. Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a) \[\frac{5y}{7}=\frac{20xy}{28x}\] b) \[\frac{3x(x+5)}{2(x+5)}=\frac{3x}{2}\]
c) \[\frac{x+2}{x-1}=\frac{(x+2)(x+1)}{{{x}^{2}}-1}\] d) \[\frac{{{x}^{2}}-x-2}{x+1}=\frac{{{x}^{2}}-3x+2}{x-1}\]
e) \[\frac{{{x}^{3}}+8}{{{x}^{2}}-2x+4}=x+2\]
Giải.
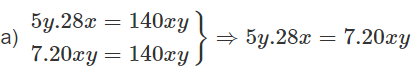
Nên \[\frac{5y}{7}=\frac{20xy}{28x}\]
b) \[3x(x+5).2=3x.2(x+5)=6x(x+5)\]
nên \[\frac{3x(x+5)}{2(x+5)}=\frac{3x}{2}\]
c) \[\frac{x+2}{x-1}=\frac{(x+2)(x+1)}{{{x}^{2}}-1}\]
Vì \[(x+2)({{x}^{2}}-1)=(x+2)(x+1)(x-1)\]
d)
\[\left( {{x}^{2}}-x-2 \right)\left( x-1 \right)=={{x}^{2}}.x+{{x}^{2}}.(-1)+(-x).x+(-x).(-1)+(-2).x+(-2).(-1)\]
\[={{x}^{3}}-{{x}^{2}}-{{x}^{2}}+x-2x+2=x3-2x2-x+2\]
\[\left( x+1 \right)\left( {{x}^{2}}-3x+2 \right)=x.{{x}^{2}}+x.\left( -3x \right)+x.2+1.{{x}^{2}}+1.\left( -3x \right)+1.2\]
\[={{x}^{3}}-3{{x}^{2}}+2x+{{x}^{2}}-3x+2=x3-2{{x}^{2}}-x+2\]
\[\Rightarrow (x2-x-2)(x-1)=(x+1)(x2-3x+2)\]
Vậy \[\frac{{{x}^{2}}-x-2}{x+1}=\frac{{{x}^{2}}-3x+2}{x-1}\]
e) \[\frac{{{x}^{3}}+8}{{{x}^{2}}-2x+4}=x+2\]
Vì \[{{x}^{3}}+8={{x}^{3}}+{{2}^{3}}=(x+2)(x22x+4)\]
Bài 2. Ba phân thức sau có bằng nhau không?
\[\frac{{{x}^{2}}-2x-3}{{{x}^{2}}+x};\frac{x-3}{x};\frac{{{x}^{2}}-4x+3}{{{x}^{2}}-x}\]
Giải.
Ta có:
\[({{x}^{2}}-2x-3)x={{x}^{3}}-2{{x}^{2}}-3x\]
\[({{x}^{2}}+x)(x-3)={{x}^{3}}-3{{x}^{2}}+{{x}^{2}}-3x=={{x}^{3}}-2{{x}^{2}}-3x\]
Nên \[({{x}^{2}}2x3)x=({{x}^{2}}+x)(x3)\]
do đó: \[\frac{{{x}^{2}}-2x-3}{{{x}^{2}}+x}=\frac{x-3}{x}\]
\[\left( x-3 \right)({{x}^{2}}-x)={{x}^{3}}-{{x}^{2}}-3{{x}^{2}}+3x\left( x-3 \right)({{x}^{2}}-x)={{x}^{3}}-4{{x}^{2}}+3x\]
\[x({{x}^{2}}-4x+3)={{x}^{3}}-4{{x}^{2}}+3x\]
Nên \[\left( x-3 \right)({{x}^{2}}-x)=x({{x}^{2}}-4x+3)\]
do đó \[\frac{x-3}{x}=\frac{{{x}^{2}}-4x+3}{{{x}^{2}}-x}\]
Vậy: \[\frac{{{x}^{2}}-2x-3}{{{x}^{2}}+x}=\frac{x-3}{x}=\frac{{{x}^{2}}-4x+3}{{{x}^{2}}-x}\]







