Các dạng toán cơ bản phần Tứ Giác trong chương trình Sách giáo khoa Toán lớp 8
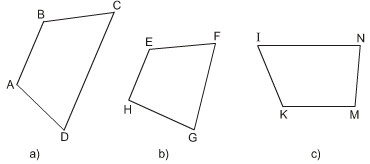
- Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình 19). Trên hình 20, có những tứ giác nào là hình thang, có những tứ giác nào không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình 20, tứ giác nào là hình thang
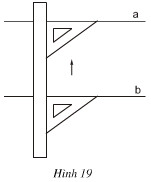
Hướng dẫn giải bài tập chi tiết:
Các bước tiến hành:
– Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.
– Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.
– Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.
– Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.
Các tứ giác ABCD, IKMN là hình thang.
Tứ giác EFGH không là hình thang.
- Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD.
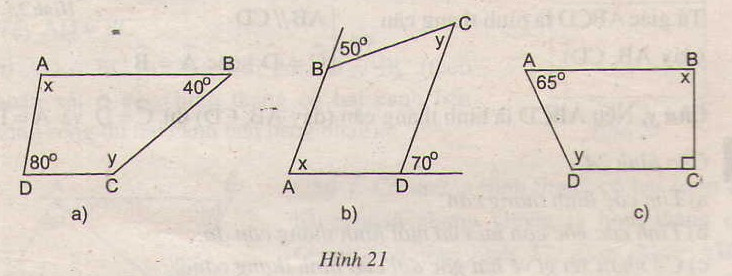
Bài giải chi tiết:
Dựa vào kiến thức hình học 8 bạn có thể áp dụng giải như sau:
a)
x = 1800 – 800 = 1000
y = 1800 – 400 = 1400
b)
x = 700 (đồng vị)
y = 500 (so le trong)
c)
x = 1800 – 900 = 900
y = 1800 – 650 = 1150
Một số dạng toán lớp 8 cơ bản phần Hình học với lời giải đơn giản nhất
1. Hình thang ABCD ( AB // CD) có \[\widehat{A}-\widehat{D}={{20}^{0}}\], \[\widehat{B}=2\widehat{C}\]. Tính các góc của hình thang
Giải
Ta có: \[\widehat{A}-\widehat{D}={{20}^{0}}\];\[\widehat{A}+\widehat{D}={{180}^{0}}\]
Từ \[\widehat{A}-\widehat{D}={{20}^{0}}\] \[\Rightarrow \widehat{A}={{20}^{0}}+\widehat{D}\]
Nên \[\widehat{A}+\widehat{D}={{20}^{0}}+\widehat{D}+\widehat{D}={{180}^{0}}\]
\[\Rightarrow \widehat{D}={{80}^{0}}\]
Thay \[\widehat{D}={{80}^{0}}\] vào \[\widehat{A}={{20}^{0}}+\widehat{D}\] ta được \[\widehat{A}={{20}^{0}}+{{80}^{0}}={{100}^{0}}\]
Lại có: \[\widehat{B}=2\widehat{C}\]; \[\widehat{B}+\widehat{C}={{180}^{0}}\]
Nên \[2\widehat{C}+\widehat{C}={{180}^{0}}\]
Hay \[3\widehat{C}={{180}^{0}}\Rightarrow \widehat{C}={{60}^{0}}\]
Do đó \[\widehat{B}=2\widehat{C}={{2.60}^{0}}={{120}^{0}}\]
9. Tứ giác ABCD có AB = BC và tia phân giác của góc A. Chứng minh rằng ABCD là hình thang
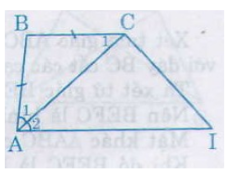
Ta có: AB = AC (gt)
Suy ra \[\Delta ABC\] cân
Nên \[\widehat{{{A}_{1}}}=\widehat{{{C}_{1}}}(1)\]
Lại có \[\widehat{{{A}_{1}}}=\widehat{{{A}_{2}}}(2)\] ( Vì AC là tia phân giác của \[\widehat{A}\])
Từ (1) và (2) suy ra \[\widehat{{{C}_{1}}}=\widehat{{{A}_{2}}}\]
Nên BC // AD ( do \[\widehat{{{C}_{1}}}\], \[\widehat{{{A}_{2}}}\] ở vị trí so le trong)
Vậy ABCD là hình thang
10. Đố hình 22 là hình vẽ một chiếc thang trên hình vẽ có bao nhiêu hình thang?
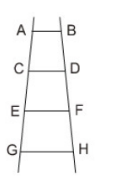
Bài giả: có tất cả 6 hình thang, dó là: ABCD, CDFE, EFHG, ABFE, CDHG, ABHG







