Chuyên đề: Áp dụng mệnh đề vào suy luận toán học

§2. ÁP DỤNG MỆNH ĐỀ VÀO SUY LUẬN TOÁN HỌC

TÓM TẮT LÍ THUYẾT

Định lí và chứng minh định lí:

Trong Toán học, định lí là một mệnh đề đúng. Nhiều định lí được phát biểu dưới dạng: \[''\forall x\in X,P(x)\Rightarrow Q(x)''\], P(x), Q(x) là các mệnh đề chứa biến
Có 2 cách để chứng minh định lí dưới dạng trên

Cách 1: Chứng minh trực tiếp gồm các bước sau:

Lấy x \[\in \]X bất kỳ mà P(x) đúng.
Chứng minh Q(x) đúng bằng suy luận và kiến thức Toán học đã biết.

Cách 2: Chứng minh bằng phản định lí gồm các bước sau:

Giả sử tồn tại \[{{x}_{0}}\in X\]sao cho P(x₀) đúng là Q(x₀) sai
Dùng suy luận và các kiến thức toán học để đi đến mâu thuẫn.

Định lí đảo, điều kiện cần, điều kiện đủ, điều kiện cần và đủ:

Cho định lí dưới dạng \[''\forall x\in X,P(x)\Rightarrow Q(x)''\] (1). Khi đó

P(x) là điều kiện đủ để có Q(x)

Q(x) là điều kiện cần đề có P(x)

Mệnh đề \[''\forall x\in X,Q(x)\Rightarrow P(x)''\] đúng thì được gọi là định lí đảo của định lí dạng (1)

Lúc đó (1) được gọi là định lí thuận và khi đó có thể gộp lại thành một định lí \[''\forall x\in X,Q(x)\Leftrightarrow P(x)''\], ta gọi là P(x) là điều kiện cần và đủ để có Q(x).

Ngoài ra còn nói “P(x) nếu và chỉ nếu Q(x)”, “P(x) khi và chỉ khi Q(x)”.

CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.

DẠNG TOÁN 1: PHƯƠNG PHÁP CHỨNG MINH BẰNG PHẢN CHỨNG

& 1. CÁC VÍ DỤ MINH HỌA

Ví dụ 1: Chứng minh rằng với mọi số tự nhiên n, n³ chia hết cho 3 thì n chia hết cho 3

Lời giải

Giả sử n không chia hết cho 3 khi đó n = 3k + 1 hoặc n = 3k + 2, k\[\in \mathbb{Z}\]

Với n = 3k + 1 ta có n³ = (3k +1)³ = 27k³ + 27k² + 9k + 1 không chia hết cho 3 (mâu thuẫn)

Với n = 3k + 2 ta có n³ = (3k +2)³ = 27k³ + 54k² + 36k + 4không chia hết cho 3 (mâu thuẫn)

Vậy n chia hết cho 3.

Ví dụ 2: Cho tam thức f(x) = ax² + bx + c, a\[\ne \]0. Chứng minh rằng nếu tồn tại số thực \[\alpha \]sao cho a.f(\[\alpha \]) ≤ 0 thì phương trình f(x) = 0 luôn có nghiệm.

Lời giải

Ta có \[f(x)=a{{\left( x+\frac{b}{2a} \right)}^{2}}-\frac{\Delta }{4a},\Delta ={{b}^{2}}-4ac\].

Giả sử phương trình đã cho vô nghiệm, nghĩa là Δ < 0.

Khi đó t có \[af(x)={{a}^{2}}{{\left( x+\frac{b}{2a} \right)}^{2}}-\frac{\Delta }{4}>0,\forall x\in \mathbb{R}\]

Suy ra không tồn tại \[\alpha \]sao cho a.f(\[\alpha \]) ≤ 0, trái với giả thiết.

Vậy điều ta giả sử ở trên là sai, hay phương trình đã cho luôn có nghiệm.

Ví dụ 3: Chứng minh rằng một tam giác có đường trung tuyến vừa là phân giác xuất phản từ một đỉnh là tam giác cân tại đỉnh đó.

Lời giải

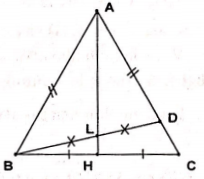
Giả sử tam giác ABC có AH vừa là đường trung tuyến vừa là đường phân giác và không cân tại A.

Không mất tính tổng quát xem như AC > AB

Trên AC lấy D sao cho AB = AD.

Gọi L là giao điểm của BD và AH.

Khi đó AB = AD, \[\widehat{BAL}=\widehat{LAD}\] và AL chung nên ΔABL = ΔADL

Do đó AL = LD hay L là trung điểm của BD

Suy ra LH là đường trung bình của ΔCBD

\[\Rightarrow \]LH//DC điều này mâu thuẫn vì LH, DC cắt nhau tại A

Vậy tam giác ABC cân tại A.

& 2. BÀI TẬP LUYỆN TẬP

Bài 1.12: Chứng minh bằng phương pháp phản chứng: Nếu phương trình bậc hai : ax² + bx + c = 0 vô nghiệm thì a và c cùng dấu.

Hướng dẫn giải

Giả sử phương trình vô nghiệm và a, c trái dấu . Với điều kiện a, c trái dấu ta có a.c < 0 suy ra Δ = b²– 4ac = b² + 4(-ac) > 0

Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm.

Vậy phương trình vô nghiệm thì a, c phải cùng dấu.

Bài 1.13: Chứng minh bằng phương pháp phản chứng: Nếu hai số nguyên dương có tổng bình phương chia hết cho 3 thì cả hai số đó phải chia hết cho 3.

Hướng dẫn giải

Giả sử trong hai số nguyên dương a và b có ít nhất một số không chia hết cho 3, chẳng hạn a không chia hết cho 3. Thế thì a có dạng a = 3k + 1 hoặc a = 3k + 2. Lúc đó a²= 3m + 2, nên nếu b chia hết cho 3 hoặc b không chia hết cho 3 thì a² + b² cũng có dạng 3n + 1 hoặc 3n + 2, tức là a² + b² không chia hết cho 3, trái giả thiết. Vậy nếu a² + b² chia hết cho 3 thì cả a và b đều chia hết cho 3.

Bài 1.14: Chứng minh rằng: Nếu độ dài các cạnh của tam giác thỏa mãn bất đẳng thức a² + b² > 5c² thì c là dộ dài cạnh nhỏ nhất của tam giác.

Hướng dẫn giải

Giả sử c không phải là cạnh nhỏ nhất của tam giác.

Không mất tính tổng quát, giả sử a ≤ c \[\Rightarrow \]a² ≤ c² (1)

Theo bất đẳng thức trong tam giác, ta có, b < a + c \[\Rightarrow \]b² < (a +c)² (2).

Do a ≤ c \[\Rightarrow \]( a +c)² ≤ 4c² (3)

Từ (2) và (3) suy ra b² ≤ 4c² (4)

Cộng vế với vế (1) và (4) ta có a² + b² ≤ 5c² mâu thuẫn với giả thiết

Vậy c là cạnh nhỏ nhất của tam giác.

Bài 1.15: Cho a, b, c dương nhỏ hơn 1. Chứng minh rằng ít nhất một trong ba bất đẳng thức sau sai \[a(1-b)>\frac{1}{4}\], \[b(1-c)>\frac{1}{4}\],\[c(1-a)>\frac{1}{4}\]

Hướng dẫn giải

Giả sử cả ba bất đẳng thức đều đúng.

Khi đó, nhân vế theo vế của các bất đẳng thức trên ta được:

\[a(1-b).b(1-c).c(1-a)>{{\left( \frac{1}{4} \right)}^{3}}\]hay \[a(1-a).b(1-b).c(1-c)>\frac{1}{64}\](*)

Mặt khác \[a(1-a)=-{{a}^{2}}+a=\frac{1}{4}-{{\left( a-\frac{1}{2} \right)}^{2}}\le \frac{1}{4}\]

Do 0 < a < 1\[\Rightarrow 0

Tương tự thì \[\Rightarrow 0

Nhân vế theo vế ta được \[a(1-a).b(1-b).c(1-c)\le \frac{1}{64}\] (**)

Bất đẳng thức (**) mâu thuẫn với (*)

Vậy có ít nhất một trong ba bất đẳng thức đã cho là sai. (đpcm)

Bài 1.16: Nếu a₁a₁ ≥ 2 (b₁ + b₂) thì ít nhất một trong hai phương trình x² + a₁x + b₁ = 0, x² + a₂x + b₂ = 0 có nghiệm.

Hướng dẫn giải

Giả sử cả hai phương trình trên vô nghiệm

Khi đó D₁ = a₁² – 4b₁ < 0, D₂ = a₂² – 4b₂

\[\Rightarrow \] a₁² – 4b₁ + a₂² – 4b₂ < 0 \[\Leftrightarrow \] a₁² + a₂²< 4(b₁ + b₂) (1)

Mà (a₁ + a₂)² ≥ 0 \[\Leftrightarrow \] a₁² + a₂²≥ 2a₁a₂(2)

Từ (1) và (2) suy ra 2a₁a₂ < 4 (b₁ + b₂) hay a₁a₂ < 2(b₁ + b₂) trái giả thiết

Vậy phải có ít nhất một trong hai sô Δ₁, Δ₂ lớn hơn 0 do đó ít nhất 1 trong 2 phương trình x² + a₁x + b₁ = 0, x² + a₂x + b₂ = 0 có nghiệm.

Bài 1.17: Chứng minh rằng \[\sqrt{2}\] là số vô tỉ.

Hướng dẫn giải

Dễ dàng chứng minh được nếu n² là số chẵn thì n là số chẵn.

Giả sử \[\sqrt{2}\] là số hữu tỉ, tức là \[\sqrt{2}=\frac{m}{n}\], trong đó m, n \[\in \mathbb{N}*\], (m, n) = 1

Từ \[\sqrt{2}=\frac{m}{n}\] \[\Rightarrow \]m² = 2n^{2\[\Rightarrow \]}m² là số chẵn

\[\Rightarrow \]m là số chẵn \[\Rightarrow \]m = 2k, k \[\in \mathbb{N}*\]

Từ m² = 2n^{2\[\Rightarrow \]}4k² = 2n^{2 \[\Rightarrow \]}n² = 2k^{2\[\Rightarrow \]}n² là số chẵn \[\Rightarrow \]n là số chẵn

Do đó m chẵn, n chẵn mâu thuẫn với (m, n) = 1.

Vậy \[\sqrt{2}\] là số vô tỉ.

Bài 1.18: Cho các số a, b, c thỏa mãn các điều kiện:

a+b+c>0(1)

ab+bc+ca>0(2)

abc>0(3)

Chứng minh rằng cả ba số a, b, c đều dương.

Hướng dẫn giải

Giả sử cả ba số a, b, c không đồng thời là số dương. Vậy có ít nhất một số không dương.

Do a, b, c có vai trò bình đẳng nên ta có thể giả sử a: ≤ 0

+ Nếu a = 0 mâu thuẫn với (3)

+ Nếu a < 0 thì từ (3) suy ra bc < 0

Ta có (2) \[\Leftrightarrow \]a(b +c) > -bc \[\Rightarrow \]a(b +c) > 0

\[\Rightarrow \]b + c < 0 \[\Rightarrow \]a + b + c < 0 mâu thuẫn (1).

Vậy cả ba số a, b, c đều dương.

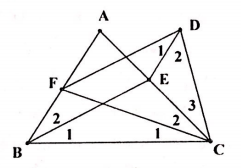
Bài 1.19: Chứng minh bằng phản chứng định lí sau: “Nếu tam giác ABC có các đường phân giác trong BE, CF bằng nhau thì tam giác ABC cân”.

Hướng dẫn giải

Xét tam giác BCE và CBF, ta thấy:

BC chung, BE = CF, BF > CE nên \[\widehat{{{C}_{1}}}>\widehat{{{B}_{1}}}\Rightarrow \widehat{C}>\widehat{B}\]. Mâu thuẫn

Trường hợp \[\widehat{C}>\widehat{B}\], chứng minh hoàn toàn tương tự như trên.

Do đó \[\widehat{B}=\widehat{C}\]. Vậy tam giác ABC cân tại A.

Bài 1.20: Cho 7 đoạn thẳng có độ dài lớn hơn 10 và nhỏ hơn 100. Chứng minh rằng luôn tìm được 3 đoạn để có thể ghép thành một tam giác.

Hướng dẫn giải

Trước hết sắp xếp các đoạn đã cho theo thứ tự tăng dần của độ dài a₁, a₂,…,a₇và chứng minh rằng trong dãy đã sắp xếp luôn tìm được 3 đoạn liên tiếp sao cho tổng của 2 đoạn đầu hớn hơn đoạn cuối (vì điều kiện để 3 đoạn có thể ghép thành một tam giác là tổng của hai đoạn lớn hơn đoạn thứ 3).

Giả sử điều kiện cần chứng minh là không xảy ra, nghĩa là đồng thời xảy ra các bất đẳng thức sau: a₁ + a₂ ≤ a₃; a₂ + a₃≤ a₄;…; a₅ + a₆ ≤ a₇.

Từ giả thiết a₁, a₂ có giá trị lớn hơn 10, ta nhận được a₃ > 20. Từ a₂ >10 và a₃ > 20 ta nhận được a₄ >30, a₅> 50, a₆ > 80 và a₇ > 130. Điều a₇ > 130 là mâu thuẫn với giả thiết các độ dài nhỏ hơn 100. Có mâu thuẫn này là do giả sử điều cần chứng minh không xảy ra.

Vậy, luôn tồn tại 3 đoạn liên tiếp sao cho tổng của 2 đoạn đầu hớn hơn đoạn cuối. Hay nói cách khác là 3 đoạn này có thể ghép thành một tam giác.

DẠNG TOÁN 2: SỬ DỤNG THUẬT TOÁN ĐIỀU KIỆN CẦN, ĐIỀU KIỆN ĐỦ, ĐIỀU KIỆN CẦN VÀ ĐỦ

& 1. CÁC VÍ DỤ MINH HỌA

Ví dụ 1: Cho định lí: “Cho số tự nhiên n, nếu n⁵ chia hết cho 5 thì n chia hết cho 5”. Định lí này được viết theo dạng P \[\Rightarrow \]Q.

Hãy xác định các mệnh đề P và Q.
Phát biểu định lí trên bằng cách dung thuật ngữ “điều kiện cần”.
Phát biểu định lí trên bằng cách dung thuật ngữ “điều kiện đủ”.
Hãy phát biểu định lí đảo (nếu có) của định lí trên rồi dung các thuật ngữ “điều kiện cần và đủ” để gộp cả hai định lí thuận và đảo.

Lời giải

P: “n là số tự nhiên, n⁵ chia hết cho 5”, Q: “n chia hết cho 5”.
Với n là số tự nhiên, n chia hết cho 5 là điều kiện cần đề n⁵ chia hết cho 5; hoặc phát biểu các khác : Với n là số tự nhiên, điều kiện cần đề n⁵ chia hết cho 5 là n chia hết cho 5.
Với n là số tự nhiên, n⁵ chia hết cho 5 là điều kiện đủ để n chia hết cho 5.
Định lí đảo: “Cho số tự nhiên n, nếu n chia hết cho 5 thì n⁵ chia hết cho 5”.
Thật vậy nếu n = 5k thì n⁵ = 5⁵.k⁵: số này chia hết cho 5.

Điều kiện cần và đủ để n chia hết cho 5 là n⁵ chia hết cho 5.

Ví dụ 2: Phát biểu các mệnh đề sau với thuật ngữ “Điều kiện cần”, “Điều kiện đủ”

Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau
Nếu số nguyên dương chia hết cho 6 thì chia hết cho 3
Nếu hình thang có hai đường chéo bằng nhau thì nó là hình thang cân
Nếu tam giác ABC vuông tại A và AH là đường cao thì AB² = BC.AH

Lời giải

Hai tam giác bằng nhau là điều kiện đủ để chúng có diện tích bằng nhau

Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau.

Số nguyên dương chia hết cho 6 là điều kiện đủ để nó chia hết cho 3

Số nguyên dương chia hết cho 3 là điều kiện cần để nó chia hết cho 6

Hình thang có hai đường chéo bằng nhau là điều kiện đủ để nó là hình thang cân

Hình thang cân là điều kiện cần để nó có hai đường chéo bằng nhau

Tam giác ABC vuông tại A và AH là đường cao là điều kiện đủ để AB² = BC.AH

Tam giác ABC có AB² = BC.AH là điều kiện cần để nó vuông tại A và AH là đường cao.

& 2. BÀI TẬP LUYỆN TẬP

Bài 1.21: Phát biểu các định lí sau đây bằng cách sử dụng khái niệm “Điều kiện cần” và “Điều kiện đủ”

Nếu trong mặt phẳng, hai đường thẳng cùng vuông góc với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau.
Nếu số nguyên dương có chữ số tận cùng là 5 thì chia hết cho 5.
Nếu tứ giác là hình thoi thì hai đường chéo vuông góc với nhau.
Nếu hai tam giác bằng nhau thì chúng có các góc tương ứng bằng nhau.
Nếu số nguyên dương a chia hết cho 24 thì chia hết cho 4 và 6.

Hướng dẫn giải

Trong mặt phẳng, hai đường thẳng cùng vuông góc với đường thẳng thứ 3 là điều kiện đủ để hai đường thẳng đó song song với nhau

Trong mặt phẳng, hai đường thẳng song song với nhau là điều kiện cần để hai đường thẳng đó cùng vuông góc với đường thẳng thứ 3.

Số nguyên dương có chữ số tận cùng là 5 là điều kiện đủ để chia hết cho 5.

Số nguyên dương chia hết cho 5 là điều kiện cần để có chữ số tận cùng là 5.

Tứ giác là hình thoi là điều kiện đủ để hai đường chéo vuông góc với nhau.

Tứ giác có hai đường chéo vuông góc với nhau là điều kiện cần để nó là hình thoi.

Hai tam giác bằng nhau là điều kiện đủ để chúng có các góc tương ứng bằng nhau.

Hai tam giác có các góc tương ứng bằng nhau là điều kiện cần để chúng bằng nhau.

Số nguyên dương a chia hết cho 24 là điều kiện đủ để nó chia hết cho 4 và 6.

Số nguyên dương a chia hết cho 4 và 6 là điều kiện cần để nó chia hết cho 24.

Bài 1.22: Dùng thuật ngữ điều kiện cần và đủ để phát biểu các thuật ngữ sau

Một tam giác là tam giác cân, nếu và chỉ nếu nó có hai góc bằng nhau
Tứ giác là hình bình hành khi và chỉ khi tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
\[x\ge y\Leftrightarrow \sqrt[3]{x}\ge \sqrt[3]{y}\]
Tứ giác MNPQ là hình bình hành khi và chỉ khi \[\overrightarrow{MN}=\overrightarrow{PQ}\].

Hướng dẫn giải

Một tam giác là tam giác cân là điều kiện cần và đủ để nó có hai góc bằng nhau
Tứ giác là hình bình hành là điều kiện cần và đủ để tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
\[x\ge y\]là điều kiện cần và đủ để \[\sqrt[3]{x}\ge \sqrt[3]{y}\]
Điều kiện cần và đủ để tứ giác MNPQ là hình bình hành là \[\overrightarrow{MN}=\overrightarrow{PQ}\].

Bài 1.23: Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ” để phát biểu định lí sau: