Chuyên đề: Chứng minh đường thẳng là tiếp tuyến đường tròn.

Chuyên đề: Chứng minh đường thẳng là tiếp tuyến đường tròn

A. Lý thuyết

Phương pháp 1: Chứng minh khoảng cách từ tâm O đến đường thẳng (d) bằng bán kính R (Phương pháp này thường được dung khi chưa biết giao điểm của (d) và (O) ).
Phương pháp 2: Nếu biết đường thẳng (d) và (O) có một giao điểm A. Ta chỉ cần chứng minh minh $OA\bot d$.
Phương pháp 3: (Phương pháp trùng khít). Để chứng minh một đường thẳng (d) là tiếp tuyến của (O) ta dựng đường thẳng (d’) là tiếp tuyến của (O) sau đó chứng minh (d) và (d’) trùng nhau. Do đó (d) là tiếp tuyến của (O).

B. Bài tập

I. Bài tập minh họa

Câu 1: Cho tam giác ABC có AB=3, AC=4, BC=5. Vẽ đường tròn (B;BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.

Hướng dẫn giải

Ta có: $B{{C}^{2}}={{5}^{2}}=25;A{{B}^{2}}+A{{C}^{2}}={{3}^{2}}+{{4}^{2}}=25\Rightarrow B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}$

$\Rightarrow \Delta ABC$ vuông tại A $\Rightarrow AB\bot AC$

Suy ra: AC là tiếp tuyến của (B;BA).

Câu 2: Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm AI. Chứng minh: MF là tiếp tuyến của (O).

Hướng dẫn giải

Ta chứng minh được I là trực tâm của tam giác ABC.

Trong tam giác vuông AFI có FM là trung tuyến nên MF = MA = MI, suy ra tam giác MFA cân tại M, suy ra $\widehat{AFM}=\widehat{MAF}$.

Ta có: $\widehat{OFC}=\widehat{FCO}$ (Tam giác OCF cân tại O).

Từ đó: \[\widehat{AFM}+\widehat{OFC}=\widehat{MAF}+\widehat{OCF}={{90}^{0}}\]. Suy ra $\widehat{MFO}={{90}^{0}}$ Vậy \[OF\bot FM,F\in \left( O \right)\] nên MF là tiếp tuyến của (O).

Câu 3: Cho đường tròn (O) đường kính AB. Ax, By là 2 tia tiếp tuyến của (O) (Ax, By cùng nửa mặt phẳng bờ là đường thẳng AB). Trên Ax lấy điểm C, trên By lấy điểm D sao cho $\widehat{COD}={{90}^{0}}$. Chứng minh rằng: CD tiếp xúc với đường tròn (O).

Hướng dẫn giải

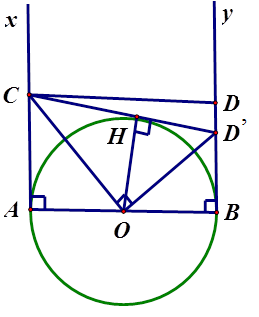
Từ C vẽ tiếp tuyến CD’ của đường tròn (O) (D’ thuộc By) tiếp xúc với (O) tại tiếp điểm H.

Ta có: OC là phân giác của $\widehat{AOH}$(t/c hai tiếp tuyến cắt nhau)

Và OD’ là phân giác của góc BOH.

Mà hai góc AOH và BOH là hai góc kề bù nên \[\widehat{OCD}\text{ }=\text{ }{{90}^{0}}\].

Ta có \[\widehat{COD}\text{ }=\widehat{COD}=\text{ }{{90}^{0}}\]. Mà D, D’ đều thuộc By nên suy ra ${D}'\equiv D$.

Vì CD’ là tiếp tuyến của (O) $\Rightarrow $ CD cũng là tiếp tuyến của (O).

Câu 4: Cho đường tròn (O; 3cm) và điểm A trên đường tròn. Qua A kẻ tiếp tuyến Ax, trên đó lấy đó lấy điểm B sao cho AB=OA.

a) Tính độ dài đoạn OB

b) Gọi I là trung điểm của đoạn OB, AI cắt đường tròn (O) ở C. Tứ giác CBAO là hình gì? Vì sao?

c) Chứng minh BC là tiếp tuyến của đường tròn (O).

Hướng dẫn giải

a) $OB=2\sqrt{3}\,cm$

b) Ta có: $OB\bot AC$

$\Delta AOC$cân tại O$\Rightarrow OABC$ là hình vuông.

c) Theo câu b tứ giác OABC là hình vuông $\Rightarrow OC\bot BC$

$\Rightarrow $ BC là tiếp tuyến của (O).

Câu 5: Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm.

a) Chứng minh rằng CB là tiếp tuyến của đường tròn

b) Cho bán kính của đường tròn bằng 15cm, AB=24cm. Tính độ dài OC.

Hướng dẫn giải

a) Ta có: $OC\bot AB$ $\Rightarrow $ OC là đi qua trung điểm của AB.

$\Rightarrow $OC là đường cao đồng thời là trung tuyến của $\Delta ABC$.

$\Rightarrow \Delta ABC$ cân tại C.

$\Rightarrow $ $\Rightarrow \Delta AOC=\Delta BOC\left( c-g-c \right)$.

$\Rightarrow OB\bot BC$

$\Rightarrow $BC là tiếp tuyến của (O)

b) OC=22,5cm

II. Bài tập tự luyện

Câu 1: Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chứng minh rằng DE là tiếp tuyến chung của (I) và (J).

Câu 2: Cho tam giác ABC nhọn, đường cao BD và CE cắt nhau tại H. Gọi I là trung điểm của BC. Chứng minh rằng ID, IE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE.

Câu 3: Cho nửa đường tròn (O) đường kính AB= 2R, dây cung AC. Gọi M là điểm chính giữa cung AC. Đường thẳng kẻ từ C song song với BM cắt tia AM ở K và cắt tia OM ở D. OD cắt AC tại H.

1. Chứng minh tứ giác CKMH nội tiếp.

2. Chứng minh CD = MB và DM = CB.

3. Xác định vị trí điểm C trên nửa đường tròn (O) để AD là tiếp tuyến của nửa

đường tròn.

4. Trong trường hợp AD là tiếp tuyến cửa nửa đường tròn (O), tính diện tích phần

tam giác ADC ở ngoài đường tròn (O) theo R.

Câu 4: Cho tam giác nhọn ABC có \[\widehat{B}\text{ }=\text{ }{{45}^{0}}\]. Vẽ đường tròn đường kính AC có tâm O, đường tròn này cắt BA và BC tại D và E.

1. Chứng minh AE = EB.

2. Gọi H là giao điểm của CD và AE. Chứng minh rằng đường trung trực của đoạn HE đi qua trung điểm I của BH.

3. Chứng minh OD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDE.

Câu 5: Cho đường tròn (O) đường kính AB. C là một điểm thay đổi trên đường tròn (O). Tiếp tuyến của (O) tại C cắt AB tại D. Qua O vẽ đường thẳng vuông góc với phân giác góc ODC, đường này cắt CD tại M. Chứng minh rằng đường thẳng d qua M song song với AB luôn tiếp xúc với (O) khi C thay đổi.

Hướng dẫn giải

Câu 1:

Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh

$ID\bot DE$ hay \[\widehat{DOE}\text{ }=\text{ }{{90}^{0}}\]^.Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có:\[\widehat{BDH}\text{ }=\widehat{CEH}\text{ }=\text{ }{{90}^{0}}\].

\[\Rightarrow \] Tứ giác ADHE là hình chữ nhật.

Gọi O là giao điểm của AH và DE, khi đó ta có OD = OH = OE = OA.

\[\Rightarrow \] \[\Delta ODH\] cân tại O \[\Leftrightarrow \widehat{ODH}\text{ }=\widehat{OHD}\]

Ta cũng có \[\Delta IDH\] cân tại I\[\Leftrightarrow \widehat{IDH}\text{ }=\widehat{IHD}\].

\[\Rightarrow \widehat{IDO\text{ }}=\text{ }{{90}^{0}}\Leftrightarrow ID\bot DE\]. Ta có $ID\bot DE,D\in \left( I \right)$\[\Rightarrow \]DE tiếp xúc với (I) tại D.

Chứng minh tương tự ta cũng có DE tiếp xúc với (J) tại E.

Câu 2:

Gọi O là trung điểm của AH.

Tam giác ADH vuông tại D có DO là trung tuyến nên ta có: $DO=\frac{AH}{2}=OA=OH$

Tam giác AEH vuông tại E có EO là trung tuyến nên ta có: $EO=\frac{AH}{2}=OA=OH$.

$\Rightarrow $OA = OD = OE, do đó O là tâm đường tròn ngoại tiếp tam giác ADE.

Tam giác OAD cân tại O\[\Leftrightarrow \widehat{ODA}\text{ }=\widehat{OAD}\] (1)

DBDC vuông tại D có DI là trung tuyến . Nên $DI=\frac{BC}{2}=IC$, nên tam giác ICD cân tại I.

\[\Rightarrow \widehat{IDC}\text{ }=\widehat{DCI}\] (2)

H là giao điểm hai đường cao BD và CE

\[\Rightarrow \]H là trực tâm của \[\Delta ABC\].

\[\Rightarrow \]$AH\bot BC$ tại F (3). Khi đó $\widehat{OAD}+\widehat{ICD}={{90}^{o}}$ (2)

Từ (1), (2) và (3) ta có:

\[\widehat{ODA}\text{ }+\widehat{IDC}\text{ }=\widehat{OAD}\text{ }+\widehat{ICD}\text{ }=\text{ }{{90}^{0}}\].

Ta có $OD\bot DI,\,D\in \left( O \right)\Rightarrow $ID tiếp xúc với (O) tại.

Chứng minh tương tự ta cũg có IE tiếp xúc với (O) tại E.

Câu 3:

1. $\widehat{H}+\widehat{K}={{180}^{0}}\Rightarrow $ tứ giác CKMH nội tiếp.

2. Tứ giác DMBC là hình bình hành.

3. $\Delta ADC$ có AK $\bot $ CD và DH $\bot $ AC nên M là trực tâm tam giác. Suy ra: CM $\bot $ AD

Vậy $AD\bot AB$ $\Leftrightarrow $ CM // AB $\Leftrightarrow \overset\frown{AM}=\overset\frown{BC}$.

Mà $\overset\frown{AM}=\overset\frown{MC}$ nên $\overset\frown{AM}=\overset\frown{BC}\Leftrightarrow \overset\frown{AM}=\overset\frown{MC}=\overset\frown{BC}$

$\Rightarrow $ sđ$\overset\frown{BC}$ = 60⁰.

4. Tính diện tích phần tam giác ADC ở ngoài (O) theo R:

Gọi S là diện tích phần tam giác ADC ở ngoài đường tròn (O).

S₁ là diện tích tứ giác AOCD.

S₂ là diện tích hình quạt góc ở tâm AOC.

Ta có: S = S₁ – S₂

$*$ Tính S₁:

AD là tiếp tuyến của đường tròn (O) $\Leftrightarrow \overset\frown{AM}=\overset\frown{MC}=\overset\frown{BC}={{60}^{0}}\Rightarrow \widehat{AOD}={{60}^{0}}$.

Do đó: $A\text{D}=AO.\tan {{60}^{0}}=R\sqrt{3}\Rightarrow {{S}_{A\text{D}O}}=\frac{1}{2}AD.AO=\frac{1}{2}.R\sqrt{3}.R=\frac{{{R}^{2}}\sqrt{3}}{2}$.

$\Delta AOD=\Delta COD$(c.g.c) \[\Rightarrow ~{{S}_{AOD}}=\text{ }{{S}_{COD}}\]\[\Rightarrow {{S}_{AOCD}}=\text{ }2{{S}_{ADO}}=2.~\frac{{{R}^{2}}\sqrt{3}}{2}={{R}^{2}}\sqrt{3}\].

$*$ Tính S₂:

$\overset\frown{AC}={{120}^{0}}$ $\Rightarrow $ S_{quạt AOC} = $\frac{\pi {{R}^{2}}{{.120}^{0}}}{{{360}^{0}}}$= $\frac{\pi {{R}^{2}}}{3}$

$*$ Tính S:

$S\text{ }=\text{ }{{S}_{1}}\text{- }{{S}_{2}}={{R}^{2}}\sqrt{3}-\frac{\pi {{R}^{2}}}{3}$ (đvdt)

Câu 4:

1. \[\widehat{AEC}\text{ }=\text{ }{{90}^{0}}\] (nội tiếp chắn nửa đường tròn )

\[\Rightarrow \widehat{AEB}\text{ }=\text{ }{{90}^{0}}\] ( vì là hai góc kề bù); Theo giả thiết \[\widehat{ABE}={{45}^{0}}\]

\[\Rightarrow \Delta AEB\]là tam giác vuông cân tại E \[\Rightarrow \] EA = EB.

2. Gọi K là trung điểm của HE (1); I là trung điểm của HB\[\Rightarrow \]IK là đường trung bình của tam giác HBE\[\Rightarrow \]IK // BE mà \[\widehat{AEC}\text{ }=\text{ }{{90}^{0}}\] nên BE \[\bot \] HE tại E \[\Rightarrow \] IK \[\bot \] HE tại K (2).

Từ (1) và (2) \[\Rightarrow \]IK là trung trực của HE. Vậy trung trực của đoạn HE đi qua trung điểm I của BH.

3. Theo trên I thuộc trung trực của HE \[\Rightarrow \] IE = IH mà I là trung điểm của BH \[\Rightarrow \] IE = IB.

\[\widehat{ADC}\text{ }=\text{ }{{90}^{0}}\] (nội tiếp chắn nửa đường tròn ) \[\Rightarrow \]\[\widehat{BDH}\text{ }=\text{ }{{90}^{0}}\] (kề bù \[\widehat{ADC}\]) \[\Rightarrow \]tam giác BDH vuông tại D có DI là trung tuyến (do I là trung điểm của BH)\[~\Rightarrow ID\text{ }=\text{ }\frac{1}{2}\text{ }BH\] hay ID = IB => IE = IB = ID => I là tâm đường tròn ngoại tiếp tam giác BDE bán kính ID.

Ta có \[\Delta DOC\] cân tại O (vì OD và OC là bán kính )\[\Rightarrow \widehat{{{D}_{1}}}=\widehat{{{C}_{1}}}\] (3)

\[\Delta IB\text{D}\] cân tại I (vì ID và IB là bán kính )\[~\Rightarrow \widehat{{{D}_{2}}}=\widehat{{{B}_{1}}}\] (4)

Theo trên ta có CD và AE là hai đường cao của tam giác ABC\[\Rightarrow \]H là trực tâm của tam giác ABC \[\Rightarrow \]BH cũng là đường cao của tam giác ABC\[\Rightarrow \] \[BH\bot AC\] tại F \[\Rightarrow \] \[\Delta AEB\] có \[\widehat{AFB}\text{ }=\text{ }{{90}^{0}}\].

Theo trên \[\Delta ADC\] có \[\widehat{ADC}\text{ }=\text{ }{{90}^{0}}\Rightarrow \widehat{{{B}_{1}}}=\widehat{{{C}_{1}}}\]( cùng phụ \[\widehat{BAC}\]) (5).

Từ (3), (4), (5) \[\Rightarrow \widehat{{{D}_{1}}}=\widehat{{{D}_{2}}}\] mà \[\widehat{{{D}_{2}}}+\widehat{IDH}\text{ }=\widehat{BDC}\text{ }=\text{ }{{90}^{0}}\Rightarrow \widehat{{{D}_{1}}}+\widehat{IDH}\text{ }=\text{ }{{90}^{0}}=\widehat{IDO}\Rightarrow \]OD \[\bot \] ID tại D \[\Rightarrow \] OD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDE.

Câu 5: