Đồ thị của hàm số bậc nhất
I . Lí thuyết:
1 . Đồ thị của hàm số y = ax + b ( a ≠ 0 )
Đồ thị của hàm số y = ax + b ( a ≠ 0 ) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b, song song với đường thẳng y = ax nếu b ≠ 0 và trùng với đường thẳng y = ax nếu b = 0.
Chú ý : Đồ thị hàm số bậc nhật y = ax + b (a ≠ 0 )còn được gọi là đường thẳng y = ax + b ; b được gọi là tung độ gốc của đường thẳng.
2 . Cách vẽ đồ thị hàm số bậc nhất: y = ax + b (a ≠ 0 )
- Khi b = 0 thì y = ax. Đồ thị y = ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A(1;a) ( đã biết ).
- Xét trường hợp y = ax + b với a ≠ 0 và b≠ 0.
Ta đã biết đồ thị hàm số y = ax + b là một đường thẳng , do đó về nguyên tắc ta chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng qua hai điểm đó.
+ Cách thứ nhất :
Xác định hai điểm bất kì của đồ thị, chẳng hạn :
Cho x = 1, tính được y = a + b, ta có điểm A(1 ; a + b)
Cho x = -1 , tính được y = -a + b, ta có điểm B(-1 ; b – a)
+ Cách thứ hai :
Xác định giao điểm của đồ thị với hai trục tọa độ :
Cho x = 0, tính được y = b, ta có điểm C(0;b)
Cho y = 0, tính được x = \[-\frac{b}{a}\], ta có điểm (\[-\frac{b}{a}\];0)
Vẽ đường thẳng qua A; B hoặc qua C; D ta được đồ thị của hàm số y = ax + b
Dạng đồ thị của hàm số y = ax + b (a ≠ 0 )
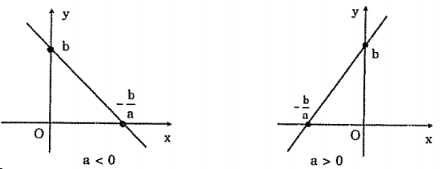
II . Bài tập ví dụ :
Ví dụ 1 : Cho các hàm số sau : y = 2x -3 và y = -3x + 4.
a, Vẽ đồ thị các hàm số trên.
b, Điểm nào sau đây thuộc đồ thị hàm số trên?
\[A\left( -\frac{1}{3};5 \right)\];\[B\left( \frac{5}{2};2 \right)\]
Giải
a,
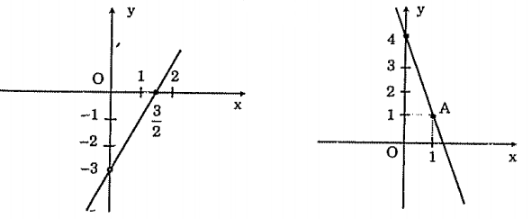
b, Thế \[{{x}_{A}}=-\frac{1}{3}\]vào hàm số y = -3x + 4 ta có \[{{y}_{A}}=-3\left( -\frac{1}{3} \right)+4\]= 5
Vậy điểm A thuộc đồ thị hàm số y = 2x – 3.
- Điểm B thuộc đồ thị hàm số y = 2x – 3.
Ví dụ 2 : a, Vẽ đồ thị các hàm số sau trên cùng mặt phẳng tọa độ:
\[y=\frac{3}{4}x-3\] và \[y=\frac{-1}{2}x+2\].
b, Gọi giao điểm của đường thẳng \[y=\frac{3}{4}x-3\,\] với các trục Oy,Ox lần lượt là A, B. Gọi giao điểm của đường thẳng \[y=\frac{-1}{2}x+2\] với trục Oy là C. Tính các góc của tam giác ABC.
Giải
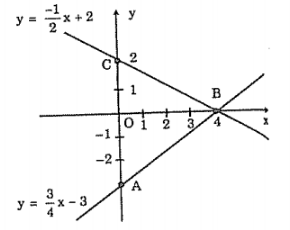a, Hình bên.
b, \[\tan \widehat{OCB}=2\Rightarrow \widehat{OCB}\approx 63{}^\circ \]
\[\tan \widehat{OAB}=\frac{4}{3}\Rightarrow \widehat{OAB}\approx 53{}^\circ \]
\[\widehat{ABC}=180{}^\circ -\left( \widehat{OCB}+\widehat{OAB} \right)=64{}^\circ \]
Ví dụ 3: Cho hàm số \[y=f(x)=\frac{2}{5}x-2\]
a, Vẽ đồ thị (D) của hàm số f(x).
b, Điểm nào sau đây nằm trên (D):
\[A\left( 1;3 \right);B\left( -5;-4 \right);C\left( \frac{5}{2};-1 \right);D\left( -2;\frac{14}{5} \right)\]
c, Tìm tọa độ điểm M ϵ (D) và N ϵ (D) khi biết : \[{{x}_{M}}=\frac{-5}{2};{{y}_{N}}=-2\].
Giải
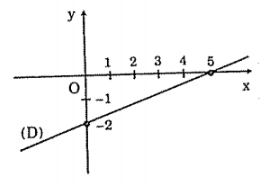a, Hình bên.
b, Điểm B và C nằm trên (D).
c, Thế \[{{x}_{M}}=\frac{-5}{2}\]vaò hàm số \[\frac{2}{5}x-2\] ta có \[{{y}_{M}}=-3\]
Vậy \[M\left( -\frac{5}{2};3 \right);N\left( 0;-2 \right)\]
III . Bài tập tự luyện :
Bài 1: a, Vẽ đồ thị các hàm số : y = x – 3; y = 3x – 3; y = -2x -3 Trên cùng một mặt phẳng tọa độ.
b, Có nhận xét gì về đồ thị các hàm số này ?
Bài 2 : Cho hàm số y = (3-2m)x – 1.
a, Với giá trị nào của m thì hàm số đồng biến?
b, Với giá trị nào của m thì hàm số nghịch biến ?
c, Xác định giá trị của m để đồ thị hàm số đi qua điểm A(-2;-3).
d, Vẽ đồ thị hàm số với giá trị m vừa tìm được ở (c).
Bài 3: a, Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau : y = 2x + 4 ; y = -x + 1 .b, Tìm tọa độ giao điểm của hai đường thẳng trên.
Bài 4 : a, Vẽ đồ thị hàm số y = x – 2 (d).
b, Tính khoangr cách từ gốc tọa độ đến đường thẳng (d).
Bài 5 : a, Vẽ trên cùng hệ trục tọa độ Oxy đồ thị hàm số sau : y = x + 4 ; y= -x + 2 .
b, Tìm tọa độ giao điểm M của hai đường thẳng;
c, Gọi giao điểm của đường thẳng y = x + 4 với trục Ox, Oy the thứ tự là A, B . Gọi giao điểm của đường thẳng y = -x +2 với Õ là C . TÍnh diện tích tam giác ABC.
Bài 6 : Vẽ tập hợp các điểm M(x;y) có tọa độ thỏa mãn phương trình : \[{{x}^{2}}+{{y}^{2}}-2xy-4=0\]
Bài 7 : a, Vẽ đồ thị của hàm số y = | x – 1 | + | x – 3 |.
b, Định giá trị của m để phương trình :
| x – 1 | + | x – 3 | = 0 có đúng một nghiệm dương.
