Các bài toán nâng cao chuyên đề hệ thức Viet

Câu 1:

cho phương trình ấn x: ${{x}^{2}}-2\left( m-1 \right)x-3-m=0$

1, Chứng tỏ rằng phương trình có nghiệm với mọi số m

2, tìm m sao cho nghiệm x₁; x₂ của phương trình thỏa mãn điều kiện

$x_{1}^{2}+x_{2}^{2}\ge 10$

Câu 2:

Gọi x₁ và x₂ là hai nghiệm của phương trình \[{{x}^{2}}-3x\text{ }+a=0\]

Gọi t₁; t₂ là hai nghiệm của phương trình \[{{t}^{2}}-12t+b=0\]

Cho biết $\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{x}_{2}}}{{{t}_{1}}}=\frac{{{t}_{1}}}{{{t}_{2}}}$ . Tính a và b

Câu 3:

Cho phương trình \[\left( m-1 \right){{x}^{2}}-2\left( m+1 \right)x+m=0\text{ }\left( 1 \right)\]

Giải và biện luận phương trình (1) theo m
Khi phương trình (1) có hai nghiệm phân biệt \[{{x}_{1}};\text{ }{{x}_{2}}\]

Tìm một hệ thức liên hệ giữa \[{{x}_{1}};\text{ }{{x}_{2}}\] độc lập đối với m
Tìm m sao cho $\left| {{x}_{1}}-{{x}_{2}} \right|\ge 2$

Câu 4:

Cho phương trình \[{{x}^{2}}+px-1=0\] (p là số lẻ) có hai nghiệm phân biệt x₁ và x₂. Chứng minh rằng nếu n là số tự nhiên thì $x_{1}^{n}+x_{2}^{n}$ và$x_{1}^{n+1}+x_{2}^{n+1}$ đều là các số nguyên và chúng nguyên tố cùng nhau.

Câu 5:

Cho x,y>0 thỏa mãn hệ thức$\sqrt{x}(\sqrt{x}+\sqrt{y})=3\sqrt{y}\left( \sqrt{x}+5\sqrt{y} \right)(1)$

Hãy tính giá trị biểu thức $E=\frac{2x+\sqrt{xy}+3y}{x+\sqrt{xy}-y}$

Câu 6:

a, Không giải phương trình này hãy tính hiệu các lập phương của các nghiệm lớn và nghiệm nhỏ của phương trình :${{x}^{2}}-\frac{\sqrt{85}}{4}x+1\frac{5}{16}=0$

b. Với giá trị nào của số nguyên a các nghiệm của phương trình

\[\text{a}{{\text{x}}^{2}}+\left( 2a-1 \right)x+a-2=0\] là các số hữu tỷ.

Câu 7:

cho phương trình \[{{x}^{2}}+~ax+b=0\] . Xác định a và b để phương trình có hai nghiệm phân biệt x₁ và x₂ thỏa mãn x₁ – x₂ =5 và $x_{1}^{3}-x_{2}^{3}=35$ .Tính các nghiệm đó

Câu 8:

cho phương trình ${{x}^{2}}-2(m-1)x+{{m}^{2}}-3m+4=0$

Xác định m để phương trình có hai nghiệm phân biệt x₁ và x₂ thỏa mãn $\frac{1}{{{x}_{1}}}+\frac{1}{{{x}_{2}}}=1$
Lập một hệ thức độc lập giữa x₁ và x₂ độc lập với m.

Câu 9:

Cho phương trình $\left( m+2 \right){{x}^{2}}-2\left( m-1 \right)x+3-m=0$

Xác định m để phương trình có hai nghiệm x₁; x₂ thỏa mãn hệ thức:

$x_{1}^{2}+x_{2}^{2}={{x}_{1}}+{{x}_{2}}$

Lập một hệ thức giữa x₁ và x₂ không phụ thuộc vào m
Viết một phương trình bậc hai có các nghiệm là:

${{X}_{1}}=\frac{{{x}_{1}}-1}{{{x}_{1}}+1};{{X}_{2}}=\frac{{{x}_{2}}-1}{{{x}_{2}}+1}$

Câu 10:

Giả sửa và b là hai số khác nhau. Chứng minh rằng nếu phương trình:

${{x}^{2}}$ \[+ax+2b=0~~\] (1)

${{x}^{2}}+bx+2a=0$ (2)

Có đúng một nghiệm chung thì các nghiệm số còn lại của (1) và (2) là nghiệm của phương trình ${{x}^{2}}+2x+ab=0$

Câu 11:

cho phương trình \[a{{x}^{2}}+bx+c=0\text{ }\left( a\ne 0 \right)\]

Chứng minh rằng điều kiện cần và đủ để phương trình có hai nghiệm mà nghiệm này gấp đôi nghiệm kia là \[9ac=2{{b}^{2}}\]

Câu 12:

Cho phương trình : có 2 nghiệm phân biệt Không giải phương trình trên, hãy lập phương trình bậc 2 có ẩn là y thoả mãn : và

Câu 13:

Cho phương trình : có 2 nghiệm . Lập hệ thức liên hệ giữa sao cho chúng không phụ thuộc vào m.

Câu 14:

Cho phương trình :

Gọi là các nghiệm của phương trình. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức sau:

Câu 15:

Xét phương trình: ${{x}^{4}}-2({{m}^{2}}+2)+5{{m}^{2}}+3=0$ (1) m là tham số.

Chứng minh rằng phương trình luôn có 4 nghiệm phân biệt với mọi m.
Gọi các nghiệm là ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ . Hãy tính theo m giá trị của biểu thức:

M=$\frac{1}{x_{1}^{2}}+\frac{1}{x_{2}^{2}}+\frac{1}{x_{3}^{2}}+\frac{1}{x_{4}^{2}}$.

Câu 16:

Cho phương trình x$^{2}$- ax + a - 1 = 0 có hai nghiệm ${{x}_{1}},{{x}_{2}}$

a) Không giải phương trình hãy tính giá trị biểu thức $M=\frac{3x_{1}^{2}+3x_{2}^{2}-3}{x_{1}^{2}{{x}_{2}}+x_{2}^{2}{{x}_{1}}}$

b) Tìm a để tổng bình phương hai nghiệm đạt GTNN ?

Câu 17:

a) Tìm m để phương trình $2{{x}^{2}}+2mx+{{m}^{2}}-2=0$ có hai nghiệm phân biệt

b) Gọi x₁; x₂ là hai nghiệm của nó, tìm GTLN của biểu thức:

$A=\left| 2{{x}_{1}}{{x}_{2}}+{{x}_{1}}+{{x}_{2}}-4 \right|$.

Câu 18:

Cho đa thức \[f(x)={{x}^{4}}+4{{x}^{3}}-2{{x}^{2}}-12x+1\] có các nghiệm là \[{{x}_{i}}\]; \[i=\overline{1,4}\]. Hãy tính tổng sau:

\[S=\underset{i=1}{\overset{4}{\mathop \Sigma }}\,\frac{2x_{i}^{2}+1}{{{(x_{i}^{2}-1)}^{2}}}\].

Câu 19:

Cho tam thức bậc hai f(x) = ax² +bx+c ( a khác 0) có hai nghiệm x₁;x₂thuộc [0;1]. Tìm giá trị lớn nhất của biểu thức :

\[A=\frac{(a-b)(2a-b)}{a(a-b+c)}\].

Câu 20:

Cho phương trình ax²+bx+c=0(1) với a>0 có hai nghiệm x₁;x₂ thuộc \[\left[ 2;+\infty \right)\]. Chứng minh rằng :

(2+\[(4a-b)(2+\sqrt{\frac{c}{a}})\ge 2(4a-2b+c)\] (1)

Câu 21:

Gỉa sử phương trình ax³ +(b-a)x²+(c-a)x-c=0(1), với \[a\ne 0\]có 3 nghiệm là độ dài 3 cạnh của một tam giác. Chứng minh rằng :

\[\frac{2a-b}{a+c-b}+\frac{a}{b}>0\](2).

Câu 22:

Xét phương trình bậc hai :

\[a{{x}^{2}}+bx+c=0,a\ne 0\].

Giả sử x₁; x₂ là các nghiệm của nó.

Tính \[{{S}_{n}}={{x}_{1}}^{n}+x_{2}^{n}\],\[n\in N\].

Câu 23:

Tìm đa thức bậc 5 có hệ số nguyên nhận số thực \[\varepsilon =\sqrt[5]{\frac{2}{5}}+\sqrt[5]{\frac{5}{2}}\] làm nghiệm.

Câu 24:

Tìm chữ số tận cùng của phần nguyên của số \[{{(5+3\sqrt{3})}^{2013}}\]

Câu 25:

Tìm m để phương trình :

\[{{x}^{4}}-(2m+3){{x}^{2}}+m+5=0\] (1)

Có các nghiệm thỏa mãn : \[-2<{{x}_{1}}<-1<{{x}_{2}}<0<{{x}_{3}}<1<{{x}_{4}}<3\] (*).

Câu 26:

Cho phương trình : \[f(x)={{x}^{2}}-(m+2)x+5m+1=0\] (1).

Tìm m sao cho:

1. 1. Phương trình chỉ có một nghiệm thỏa mãn x>1.
  2. Phương trình có ít nhất một nghiệm thỏa mãn \[\left| x \right|>4\].
  3. Phương trình có nghiệm thuộc \[\left( -1;1 \right).\]
  4. Phương trình có ít nhất một nghiệm thỏa mãn \[x<2\] .

Câu 27:

Tìm m để phương trình :

\[{{x}^{2}}-2x-m\left| x-1 \right|+{{m}^{2}}=0\] (1)

có nghiệm .

Câu 28:

Cho Cho phương trình x² – (2m-1)x + m – 1 = 0. Tìm GTLN cña $x_{1}^{2}\left( 1-x_{2}^{2} \right)+x_{2}^{2}\left( 1-4x_{1}^{2} \right)$

Câu 29:

Giả sử x₁, x₂ là nghiệm của phương trình

2008x² - (2008m - 2009)x - 2008 = 0

Chứng minh

A= $\frac{3}{2}{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+2{{\left( \frac{{{x}_{1}}-{{x}_{2}}}{2}+\frac{1}{{{x}_{1}}}-\frac{1}{{{x}_{2}}} \right)}^{2}}\ge 24$

Câu 30:

Cho ba số a, b, c thoả mãn điều kiện sau:

a > 0, a² = bc, a + b + c = abc. Chứng minh rằng:

Lời giải chi tiết

Câu 1:

Ta có: ${{x}^{2}}-2\left( m-1 \right)x-3-m=0$

Có

Với mọi giá trị của m

Suy ra phương trình luôn luôn có hai nghiệm phân biệt

Ta có

Câu 2:

Áp dụng định lí viet ta có:

X₁+x₂=3 và x₁x₂=a

T₁+t₂=12 và t₁t₂

Đặt k= $\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{x}_{2}}}{{{t}_{1}}}=\frac{{{t}_{1}}}{{{t}_{2}}}$⇒ x₁=kx₂ x₂=kt₁; t₁=kt₂

Thế vào và rút ra k² =$\frac{1}{4}$

Nếu k=$\frac{1}{2}$ thì a=2 và b=32
Nếu k=$-\frac{1}{2}$ thì a=-18 và b=-288

Câu 3:

Nếu m=1 $\Rightarrow $ phương trình có nghiệm x=$\frac{1}{4}$
Nếu m≠1 xét ∆’ =(m+1)² –m(m-1)=3m+1

Với m <$\frac{-1}{3}$ phương trình vô nghiệm

Với m=$\frac{-1}{3}$ phương trình có nghiệm kép

Với m>$\frac{-1}{3}$ và m≠1 phương trình có hai nghiệm phân biệt.

Áp dụng hệ thức Viet ta có:

x1+x2=2(m+1)m-1x1.x2=mm-1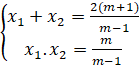 $\Rightarrow {{x}_{1}}+{{x}_{2}}-4{{x}_{1}}{{x}_{2}}+2=0$

Ta có: $$ $\left| {{x}_{1}}-{{x}_{2}} \right|\ge 2$ ⇔ ${{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}\ge 4$

$\Leftrightarrow {{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-4{{x}_{1}}{{x}_{2}}\ge 4\Leftrightarrow \frac{4{{\left( m+1 \right)}^{2}}}{{{\left( m-1 \right)}^{2}}}-\frac{4m}{m-1}\ge 4$

Giải bất phương trình ta tìm được giá trị của m

Câu 5:

Trong điều kiện (1) chia cả hai vế cho x>0 ta có:

⇔ 1+t=3t(1+5t) với t=$\sqrt{\frac{y}{x}}>0$

⇔15t²+2t-1=0 ⇔ t₁=$\frac{1}{5}$ hoặc t₂=-$\frac{1}{3}$ ( loại)

Khi t=$\frac{1}{5}$ ta chia cả tử và mẫu của E cho x>0 ta được

E=$\frac{2+t+3{{t}^{2}}}{1+t-{{t}^{2}}}=2$

Câu 6:

Gọi x₁ và x₂ (x₂ < x₁) là hai nghiệm của phương trình

Ta có: x₁+x₂=$\frac{\sqrt{85}}{4}$ và x₁x₂=1$\frac{5}{16}$

Vì x₁>x₂ $\Rightarrow {{x}_{1}}-{{x}_{2}}=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}}=\sqrt{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-4{{x}_{1}}{{x}_{2}}}$

Từ đó ta tính được $x_{1}^{3}-x_{2}^{3}=1$

Xét a=0 và a$\ne $ 0 . a=n(n+1) với n là số nguyên.

Câu 7:

Điều kiện cần: giả sử phương trình có hai nghiệm x₁; x₂ thỏa mãn điều kiện

Theo định lý Viet ta có x₁+x₂= -a và x₁x₂=b

Từ x₁ – x₂=5 ⇒

Từ $x_{1}^{3}-x_{2}^{3}=35$

Vậy từ (1) và (2) ta có hệ

Điều kiện đủ: Thay các giá trị của a và b tìm được để giải phương trình và tìm nghiệm x₁; x₂

Câu 8:

M phải thỏa mãn đồng thời

⇒ không có m thỏa mãn

Khi m≥3 phương trình có hai nghiệm phân biệt x₁ và x₂; theo định lí viet ta có:

x1+x2=2(m-1)x1.x2=m2-3m+4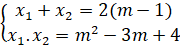

$\Rightarrow m-1=\frac{{{x}_{1}}+{{x}_{2}}}{2}$

${{x}_{1}}{{x}_{2}}={{\left( m-1 \right)}^{2}}-(m-1)+2$

$\Rightarrow {{x}_{1}}{{x}_{2}}={{\left( \frac{{{x}_{1}}+{{x}_{2}}}{2} \right)}^{2}}-\left( \frac{{{x}_{1}}+{{x}_{2}}}{2} \right)+2$

Đó là hệ thức giữa x₁ và x₂ độc lập với m.

Câu 9:

M phải thỏa mãn đồng thời:

Tìm được m=$\frac{3+\sqrt{13}}{2}$ .

Khi ∆’ ≥0 ⇔ m≤-1 hoặc m≥$\frac{5}{2}$ (m≠-2)

Ta có: x₁+x₂=$\frac{2\left( m-1 \right)}{m+2}$, x₁x₂=$\frac{3-m}{m+2}$

⇒ x₁ +x₂=2-$\frac{6}{m+2}$ , x₁x₂=-1+ $\frac{5}{m+2}$

⇒ 5(x₁+x₂) =4-6x₁x₂

Hệ thức này không phụ thuộc vào m

Ta có: X₁+X₂= $\frac{{{x}_{1}}-1}{{{x}_{1}}+1}+\frac{{{x}_{2}}-1}{{{x}_{2}}+1}=\frac{({{x}_{1}}-1)({{x}_{2}}+1)+({{x}_{2}}-1)({{x}_{1}}+1)}{({{x}_{1}}+1)({{x}_{2}}+1)}$

X₁X₂=$(\frac{{{x}_{1}}-1}{{{x}_{1}}+1}.\frac{{{x}_{2}}-1}{{{x}_{2}}+1})$

Khai triển ra, rút gọn và áp dụng định lí Viet ta có:

X₁+X₂=$\frac{2\left( 1-2m \right)}{3+2m}$ và ${{X}_{1}}.{{X}_{2}}=\frac{7-2m}{3+2m}$

Vậy X₁ và X₂ là hai nghiệm của phương trình:

$\left( 3+2m \right){{X}^{2}}-2(1-2m)X+7-2m=0$

Câu 10:

Giả sử (1) có hai nghiệm phân biệt x₁ ≠ x₀ ⇒ $x_{0}^{2}$ +ax₀ +2b=0

Có hai nghiệm phân biệt x₂ ≠ x₀ ⇒ $x_{0}^{2}$ +bx₀ +2a=0

⇒ (a-b)x₀ +2b-2a=0 ⇔ (a-b)x₀ = 2(a-b)

Vì a≠b ⇒ x₀=2 thế vào (1) ta có: 4+2a+2b=0 ⇒ a=-b-2

Thay a vào (1) ta có: x² – (b+2)x +2b=0 ⇒ (x-2)(x-b)=0

⇒ x₀=2 và x₁=b

Thayb=-a-2 vào (2), làm tương tự ta có: x₂=a

⇒ x₁+x₂=a+b và x₁x₂=ab

⇒ theo định lí đảo viet ta có x₁ và x₂là hai nghiệm của phương trình

X²-(a+b)x+ab=0 (vì a+b=-2 )⇒ x² +2x+ab=0

Câu 11:

Điều kiện cần: Giả sử phương trình có hai nghiệm x₁ và x₂ thỏa mãn hoặc x₁=2x₂ hoặc 2x₁=x₂

⇒ $\left( {{x}_{1}}-2{{x}_{2}} \right)\left( {{x}_{2}}-2{{x}_{1}} \right)=0\Rightarrow {{x}_{1}}{{x}_{2}}-2\left( x_{1}^{2}+x_{2}^{2} \right)+4{{x}_{1}}{{x}_{2}}=0$

Điều kiện đủ: Giả sử có 9ac= 2b²

Xét ∆=b²-4ac= b² -$\frac{8{{b}^{2}}}{9}=\frac{{{b}^{2}}}{9}\Rightarrow {{x}_{1}}=\frac{4b}{6a}$ và ${{x}_{2}}=-\frac{2b}{6a}$

$\Rightarrow {{x}_{1}}=2{{x}_{2}}$

Câu 12:

Theo h ệ th ức VI- ÉT ta c ó:

\[S={{y}_{1}}+{{y}_{2}}={{x}_{2}}+\frac{1}{{{x}_{1}}}+{{x}_{1}}+\frac{1}{{{x}_{2}}}=({{x}_{1}}+{{x}_{2}})+\left( \frac{1}{{{x}_{1}}}+\frac{1}{{{x}_{2}}} \right)=({{x}_{1}}+{{x}_{2}})+\frac{{{x}_{1}}+{{x}_{2}}}{{{x}_{1}}{{x}_{2}}}=3+\frac{3}{2}=\frac{9}{2}\]

\[P={{y}_{1}}{{y}_{2}}=({{x}_{2}}+\frac{1}{{{x}_{1}}})({{x}_{1}}+\frac{1}{{{x}_{2}}})={{x}_{1}}{{x}_{2}}+1+1+\frac{1}{{{x}_{1}}{{x}_{2}}}=2+1+1+\frac{1}{2}=\frac{9}{2}\]

Vậy phương trình cần lập có dạng: \[{{y}^{2}}-Sy+P=0\]

hay \[{{y}^{2}}-\frac{9}{2}y+\frac{9}{2}=0\Leftrightarrow 2{{y}^{2}}-9y+9=0\]

Câu 13:

Để phương trình trên có 2 nghiệm x₁ và x₂ th ì :

Theo hệ th ức VI- ÉT ta có :

Rút m từ (1) ta có :

\[\frac{2}{m-1}={{x}_{1}}+{{x}_{2}}-2\Leftrightarrow m-1=\frac{2}{{{x}_{1}}+{{x}_{2}}-2}\] (3)

Rút m từ (2) ta có :

\[\frac{3}{m-1}=1-{{x}_{1}}{{x}_{2}}\Leftrightarrow m-1=\frac{3}{1-{{x}_{1}}{{x}_{2}}}\] (4)

Đồng nhất các vế của (3) và (4) ta có:

\[\frac{2}{{{x}_{1}}+{{x}_{2}}-2}=\frac{3}{1-{{x}_{1}}{{x}_{2}}}\Leftrightarrow 2\left( 1-{{x}_{1}}{{x}_{2}} \right)=3\left( {{x}_{1}}+{{x}_{2}}-2 \right)\Leftrightarrow 3\left( {{x}_{1}}+{{x}_{2}} \right)+2{{x}_{1}}{{x}_{2}}-8=0\]

Câu 14:

Ta có: Theo hệ thức VI-ÉT thì :

\[\Rightarrow B=\frac{2{{x}_{1}}{{x}_{2}}+3}{x_{1}^{2}+x_{2}^{2}+2\left( {{x}_{1}}{{x}_{2}}+1 \right)}=\frac{2{{x}_{1}}{{x}_{2}}+3}{{{({{x}_{1}}+{{x}_{2}})}^{2}}+2}=\frac{2(m-1)+3}{{{m}^{2}}+2}=\frac{2m+1}{{{m}^{2}}+2}\]

Cách 1: Thêm bớt để đưa về dạng như phần (*) đã hướng dẫn

Ta biến đổi B như sau:

\[B=\frac{{{m}^{2}}+2-\left( {{m}^{2}}-2m+1 \right)}{{{m}^{2}}+2}=1-\frac{{{\left( m-1 \right)}^{2}}}{{{m}^{2}}+2}\]

Vì \[{{\left( m-1 \right)}^{2}}\ge 0\Rightarrow \frac{{{\left( m-1 \right)}^{2}}}{{{m}^{2}}+2}\ge 0\Rightarrow B\le 1\]

Vậy \[\max \text{B=1}\Leftrightarrow \] m = 1

Với cách thêm bớt khác ta lại có:

\[B=\frac{\frac{1}{2}{{m}^{2}}+2m+1-\frac{1}{2}{{m}^{2}}}{{{m}^{2}}+2}=\frac{\frac{1}{2}\left( {{m}^{2}}+4m+4 \right)-\frac{1}{2}\left( {{m}^{2}}+2 \right)}{{{m}^{2}}+2}=\frac{{{\left( m+2 \right)}^{2}}}{2\left( {{m}^{2}}+2 \right)}-\frac{1}{2}\]

Vì \[{{\left( m+2 \right)}^{2}}\ge 0\Rightarrow \frac{{{\left( m+2 \right)}^{2}}}{2\left( {{m}^{2}}+2 \right)}\ge 0\Rightarrow B\ge -\frac{1}{2}\]

Vậy \[\min B=-\frac{1}{2}\Leftrightarrow m=-2\]

Cách 2: Đưa về giải phương trình bậc 2 với ẩn là m và B là tham số, ta sẽ tìm điều kiện cho tham số B để phương trình đã cho luôn có nghiệm với mọi m.

\[B=\frac{2m+1}{{{m}^{2}}+2}\Leftrightarrow B{{m}^{2}}-2m+2B-1=0\] (Với m là ẩn, B là tham số) (**)

Ta có: \[\Delta =1-B(2B-1)=1-2{{B}^{2}}+B\]

Để phương trình (**) luôn có nghiệm với mọi m thì D ³ 0

hay \[-2{{B}^{2}}+B+1\ge 0\Leftrightarrow 2{{B}^{2}}-B-1\le 0\Leftrightarrow \left( 2B+1 \right)\left( B-1 \right)\le 0\]

Vậy: \[\max \text{B=1}\Leftrightarrow \] m = 1

\[\min B=-\frac{1}{2}\Leftrightarrow m=-2\]

Câu 15:

1) Đặt x$^{2}$ = y ( y$\ge $ 0 ) Pt (1) trở thành:

${{y}^{2}}-2({{m}^{2}}+2)y+5{{m}^{2}}+3=0$ (2)

Do \[\Delta >0,\forall m\] nên phương trình (2) luôn có hai nghiệm phân biêt.

Theo định lý Vi-et ta có:

$S={{y}_{1}}+{{y}_{2}}=\frac{-b}{a}=\frac{2({{m}^{2}}+2)}{1}=2({{m}^{2}}+2)$>0, \[\forall m\]

$P={{y}_{1}}.{{y}_{2}}=\frac{c}{a}=5{{m}^{2}}+3$>0, \[\forall m\]

$\Rightarrow {{y}_{1}},{{y}_{2}}$cùng dương.

Vậy (2) luôn có hai nghiệm dương phân biệt nên (1) luôn có 4 nghiệm phân biệt.

2) Theo kết quả trên ta có ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}\ne 0$

Vậy ${{x}_{1}}=\sqrt{{{y}_{1}}},{{x}_{2}}=-\sqrt{{{y}_{1}}}$ , ${{x}_{3}}=\sqrt{{{y}_{2}}},{{x}_{4}}=-\sqrt{{{y}_{2}}}$

$M=\frac{1}{{{(\sqrt{{{y}_{1}}})}^{2}}}+\frac{1}{{{(-\sqrt{{{y}_{1}}})}^{2}}}+\frac{1}{{{(\sqrt{{{y}_{2}}})}^{2}}}+\frac{1}{{{(-\sqrt{{{y}_{2}}})}^{2}}}$ = \[\frac{2}{{{y}_{1}}}+\frac{2}{{{y}_{2}}}\] = \[\frac{2({{y}_{1}}+{{y}_{2}})}{{{y}_{1}}+{{y}_{2}}}\]

Thay kết quả S và P vào M ta có:

$M=\frac{2.2({{m}^{2}}+2)}{5{{m}^{2}}+3}=\frac{4({{m}^{2}}+2)}{5{{m}^{2}}+3}$

Kết luận: $M=\frac{4({{m}^{2}}+2)}{5{{m}^{2}}+3}$

Câu 16:

a) Ta có: $M=\frac{3(x_{1}^{2}+x_{2}^{2}-1)}{{{x}_{1}}{{x}_{2}}({{x}_{1}}+{{x}_{2}})}=\frac{3\left[ {{({{x}_{1}}+{{x}_{2}})}^{2}}-2{{x}_{1}}{{x}_{2}}-1 \right]}{{{x}_{1}}{{x}_{2}}({{x}_{1}}+{{x}_{2}})}$

Theo định lý Vi-et ta có :

$S={{x}_{1}}+{{x}_{2}}=a;P={{x}_{1}}.{{x}_{2}}=a-1$

Vậy $M=\frac{3\left[ {{a}^{2}}-2(a-1)-1 \right]}{a(a-1)}=\frac{3\left[ (a+1)(a-1)-2(a-1) \right]}{a(a-1)}$

$=\frac{3{{(a-1)}^{2}}}{a(a-1)}=\frac{3{{(a-1)}^{2}}}{a(a-1)}=\frac{3(a-1)}{a}$ (ĐK : $a\ne 0,a\ne 1$)

b) Ta có $S={{x}_{1}}+{{x}_{2}}=a$ (1)

$P={{x}_{1}}.{{x}_{2}}=a-1$ (2)

Đặt A= x₁² +x₂² =(x₁ +x₂ )² -2x₁x₂= a² -2a+2= (a-1)²+1\[\ge \] 1

và A=1 khi a=1.

Vậy giá trị nhỏ nhất của A là 1 khi a=1.

Câu 17:

a) Ta có: ${{\Delta }^{,}}={{m}^{2}}-2({{m}^{2}}-2)=-{{m}^{2}}+4$.

Phương trình có hai nghiệm khi và chỉ khi:

\[\Delta '=4-{{m}^{2}}>0\]

b) Theo định lý Vi-et ta có :

${{x}_{1}}+{{x}_{2}}=-m;{{x}_{1}}{{x}_{2}}=\frac{{{m}^{2}}-2}{2}$

Vậy $A=\left| 2{{x}_{1}}{{x}_{2}}+{{x}_{1}}+{{x}_{2}}-4 \right|=\left| (m+2)(m-3) \right|$=\[-\left( \text{m}+\text{2} \right)\left( \text{m}-\text{3} \right)\],vì m \[\in \](-2;2)

Do đó $A=(m+2)(3-m)=-{{m}^{2}}+m+6=-{{(m-\frac{1}{2})}^{2}}+\frac{25}{4}\le \frac{25}{4}$

Vậy GTLN của A là $\frac{25}{4}$khi và chỉ khi \[m=\frac{1}{2}\].

Câu 18:

Ta viết lại :

\[f(x)={{({{x}^{2}}+2x)}^{2}}-6({{x}^{2}}+2x)+9=8\]

\[\Leftrightarrow \]\[{{({{x}^{2}}+2x-3)}^{2}}=8\]

Gọi các nghiệm của (1) là \[{{x}_{1}};{{x}_{2}}\]; các nghiệm của (2) là \[{{x}_{3}};{{x}_{4}}\].

Ta có :

\[{{S}_{1}}=\frac{2x_{1}^{2}+1}{{{(x_{1}^{2}-1)}^{_{2}}}}+\frac{2x_{2}^{2}+1}{{{(x_{2}^{2}-1)}^{_{2}}}}\]=\[\frac{2x_{1}^{2}+1}{{{(x_{1}^{{}}-1)}^{2}}{{(x_{1}^{{}}+1)}^{2}}}+\frac{2x_{2}^{2}+1}{{{(x_{2}^{{}}-1)}^{2}}{{(x_{2}^{{}}+1)}^{2}}}\]=

\[=\frac{2x_{1}^{2}+1}{{{(x_{1}^{{}}-1)}^{2}}(4-\sqrt{8})}+\frac{2x_{2}^{2}+1}{{{(x_{2}^{{}}-1)}^{2}}(4-\sqrt{8})}\]

\[=\frac{1}{(4-\sqrt{8})}\left[ \frac{(2x_{1}^{2}+1){{({{x}_{2}}-1)}^{2}}+(2x_{2}^{2}+1){{({{x}_{1}}-1)}^{2}}}{{{\left[ ({{x}_{1}}-1)({{x}_{2}}-1) \right]}^{2}}} \right]\]\[=\frac{1}{(4-\sqrt{8})}\left[ \frac{(2x_{1}^{2}+1)(x_{2}^{2}-2{{x}_{2}}+1)+(2x_{2}^{2}+1)(x_{1}^{2}-2{{x}_{1}}+1)}{{{\left[ ({{x}_{1}}{{x}_{2}}-{{x}_{1}}-{{x}_{2}}+1) \right]}^{2}}} \right]\]

\[=\frac{1}{(4-\sqrt{8})}\left[ \frac{4x_{1}^{2}x_{2}^{2}-4{{x}_{1}}{{x}_{2}}({{x}_{1}}+{{x}_{2}})+3(x_{1}^{2}+x_{2}^{2})-2({{x}_{1}}+{{x}_{2}})+2}{{{\left[ ({{x}_{1}}{{x}_{2}}-{{x}_{1}}-{{x}_{2}}+1) \right]}^{2}}} \right]\].

Áp dụng định lý Vi-et ta có: \[{{x}_{1}}+{{x}_{2}}=-2\] ; \[{{x}_{1}}{{x}_{2}}=-3+\sqrt{8}\].

Thay vào biểu thức trên ta có: \[{{S}_{1}}=\frac{1}{4+\sqrt{8}}\frac{80+22\sqrt{8}}{8}\].

Thực hiện việc tính toán tương tự đối với phương trình (2) ta có :

\[S={{S}_{1}}+{{S}_{2}}=\frac{9}{2}\].

Câu 19:

Theo định lý Vi-et ta có: \[{{x}_{1}}+{{x}_{2}}=\frac{-b}{a};{{x}_{1}}{{x}_{2}}=\frac{c}{a}\]. Biến đổi biểu thức A ta được:

\[\le 2+\frac{1+{{x}_{1}}{{x}_{2}}+{{x}_{1}}+{{x}_{2}}}{1+{{x}_{1}}+{{x}_{2}}+{{x}_{1}}{{x}_{2}}}\le \] 3.

Lại có với b=-2a=-2c thì A=3. Nên giá trị lớn nhất của A là 3.

Câu 20:

Vì x₁;x₂là hai nghiệm của (1) nên theo hệ thức Vi-et ta có:

\[{{x}_{1}}+{{x}_{2}}=\frac{-b}{a};{{x}_{1}}{{x}_{2}}=\frac{c}{a}\].

Biến đổi bất đẳng thức (1) bằng cách chia hai vế cho a ta được:

\[(4-\frac{b}{a})(2+\sqrt{\frac{c}{a}})\ge 2(4-2\frac{b}{a}+\frac{c}{a})\] \[\Leftrightarrow (4+{{x}_{1}}+{{x}_{2}})(2+\sqrt{{{x}_{1}}{{x}_{2}}})\ge 2(4+2{{x}_{1}}+2{{x}_{2}}+{{x}_{1}}{{x}_{2}})\Leftrightarrow \frac{(2+{{x}_{1}})+(2+{{x}_{2}})}{(2+{{x}_{1}})(2+{{x}_{2}})}\ge \frac{2}{2+{{\sqrt{{{x}_{1}}x}}_{2}}}\].

\[\Leftrightarrow \frac{1}{2+{{x}_{1}}}+\frac{1}{2+{{x}_{2}}}\ge \frac{2}{2+\sqrt{{{x}_{1}}{{x}_{2}}}}\Leftrightarrow \frac{1}{1+\frac{{{x}_{1}}}{2}}+\frac{1}{1+\frac{{{x}_{2}}}{2}}\ge \frac{2}{1+\sqrt{\frac{{{x}_{1}}}{2}\frac{{{x}_{2}}}{2}}}\].

Đặt \[u=\frac{{{x}_{1}}}{2};v=\frac{{{x}_{2}}}{2}\] ta thu được bất đẳng thức quen thuộc :

\[\frac{1}{1+u}+\frac{1}{1+v}\ge \frac{2}{1+\sqrt{uv}}\].

( có thể chứng minh bằng biến đổi tương đương)

Từ đó ta có điều phải chứng minh.

Câu 21:

Dễ thấy (1) có nghiệm x=1, hạ bậc ta được: (x-1)(ax²+bx+c)=0.

Gọi x₁; x₂ là các nghiệm của phương trình : ax²+bx+c=0.

Theo định lý Vi-et ta có:

\[{{x}_{1}}+{{x}_{2}}=\frac{-b}{a};{{x}_{1}}{{x}_{2}}=\frac{c}{a}\].

Biến đổi (2) như sau

\[\frac{2-\frac{b}{a}}{1+\frac{c}{a}-\frac{b}{a}}+\frac{a}{b}>0\]\[\Leftrightarrow \]\[\frac{2+{{x}_{1}}+{{x}_{2}}}{1+{{x}_{1}}+{{x}_{2}}+{{x}_{1}}{{x}_{2}}}-\frac{1}{{{x}_{1}}+{{x}_{2}}}>0\]

\[\Leftrightarrow \](2+x₁+x₂)(x₁+x₂)>(1+x₁+x₂+x₁x₂)

\[\Leftrightarrow \]x₁+x₂-1+x₁²+x₂² +x₁x₂>0.

Bất đẳng thức cuối đúng vì \[{{x}_{1}};\] \[{{x}_{2}};\] 1 là độ dài ba cạnh của tam giác.

Câu 22:

Đặt \[{{S}_{n}}={{x}_{1}}^{n}+x_{2}^{n}\],\[n\in N\].

Lúc đó ta có hệ thức truy hồi tuyến tính sau :

aS_n+2 +bS_n+1 +cS_n =0(1).

Chứng minh :

ta có :S_n+2= x₁ⁿ⁺² +x₂ⁿ⁺² = (x₁ⁿ⁺¹ + x₂ⁿ⁺¹)(x₁+x₂)- x₁x₂(x₁ⁿ + x₂ⁿ)

= S_n+1(\[\frac{-b}{a}\])-\[\frac{c}{a}\]S_n^{. \[\Leftrightarrow \]} aS_n+2 +bS_n+1 +cS_n = 0( đpcm).

Câu 23:

Ta đặt \[{{x}_{1}}=\sqrt[5]{\frac{2}{5}}\]; \[{{x}_{1}}=\sqrt[5]{\frac{5}{2}}\].

Vậy thì : \[\sqrt[5]{\frac{2}{5}}+\sqrt[5]{\frac{5}{2}}=\varepsilon \]; \[{{x}_{1}}{{x}_{2}}=1\].

Nên theo định lý Vi-et ta có \[{{x}_{1}}\]; \[{{x}_{2}}\] là nghiệm của phương trình:

\[{{x}^{2}}-\varepsilon x+1=0\] (1).

Theo hệ thức truy hồi ta có: \[{{S}_{n+2}}=\varepsilon {{S}_{n+1}}-{{S}_{n}}\] (*)

Với \[{{S}_{0}}=2\]; \[{{S}_{1}}=\varepsilon \]. Từ đó ta tính được :

\[{{S}_{2}}={{\varepsilon }^{2}}-2\]; \[{{S}_{3}}=\varepsilon ({{\varepsilon }^{2}}-2)-\varepsilon ={{\varepsilon }^{3}}-3\varepsilon \];

\[{{S}_{4}}=\varepsilon ({{\varepsilon }^{3}}-3\varepsilon )-({{\varepsilon }^{2}}-2)={{\varepsilon }^{4}}-4{{\varepsilon }^{2}}+2\]; \[{{S}_{5}}=\varepsilon ({{\varepsilon }^{4}}-4{{\varepsilon }^{2}}+2)-({{\varepsilon }^{3}}-3\varepsilon )={{\varepsilon }^{5}}-5{{\varepsilon }^{3}}+5\varepsilon \].

Nhưng mặt khác ta lại có:

\[{{S}_{5}}=\frac{2}{5}+\frac{5}{2}=\frac{29}{10}\].

Từ đó ta có được :

\[{{\varepsilon }^{5}}-5{{\varepsilon }^{3}}+5\varepsilon =\frac{29}{10}\] \[\Leftrightarrow 10{{\varepsilon }^{5}}-50{{\varepsilon }^{3}}+50\varepsilon -29=0\].

Điều đó chứng tỏ \[\varepsilon \] là nghiệm phương trình:

10x⁵ -50x³ +50x -29 =0 .

Đây chính là phương trình cần tìm.

Câu 24:

Ta đặt \[{{x}_{1}}=5+3\sqrt{3}\] ; \[{{x}_{2}}=5-3\sqrt{3}\]. Khi đó x₁ ; x₂ là nghiệm của phương trình:

x² -10x -2 = 0

Đặt \[{{S}_{n}}=x_{1}^{n}+x_{2}^{n}\]. Theo hệ thức truy hồi ta có:

\[{{S}_{n+2}}=10{{S}_{n+1}}+2{{S}_{n}}\].

Ta có S₁ =10 nên từ hệ thức trên ta suy ra S_nluôn chia hết cho 10 khi n là số lẻ.

Để ý rằng -12 <0 , nên suy ra

Vậy nên \[\left[ x_{1}^{n} \right]={{S}_{n}}\]. Vì 2013 là số lẻ nên S₂₀₁₃ chia hết cho 10.

Vậy chữ số tận cùng của phần nguyên của số \[{{(5+3\sqrt{3})}^{2013}}\] là số 0.

Câu 25:

Đây là phương trình trùng phương.

Đặt t=x². Ta đưa về phương trình : \[{{t}^{2}}-(2m+3)t+m+5=0\](2).

Để (1) có 4 nghiệm phân biệt thì (2) phải có hai nghiệm dương phân biệt.

Ta giả sử hai nghiệm của (2) là : \[0<{{t}_{1}}<{{t}_{2}}\].

Khi đó \[{{x}_{1}}=-\sqrt{{{t}_{2}}}\];\[{{x}_{2}}=-\sqrt{{{t}_{1}}}\]; \[{{x}_{3}}=\sqrt{{{t}_{1}}}\] ; \[{{x}_{4}}=\sqrt{{{t}_{2}}}\].

Do đó từ giả thiết ta có : \[-2<-\sqrt{{{t}_{2}}}<-1<-\sqrt{{{t}_{1}}}<0<\sqrt{{{t}_{1}}}<1<\sqrt{{{t}_{2}}}<3\].

\[\Leftrightarrow \] \[0<{{t}_{1}}<1<{{t}_{2}}<2\] (**).

Ta tách điều kiện (**) ra làm hai điều kiện đồng thời:

Xử lý tương tự ở trên ta có kết quả không có m nào thỏa mãn.

Câu 26:

có 3 trường hợp xảy ra:

TH1: \[{{x}_{1}}<1<{{x}_{2}}\Leftrightarrow af(1)<0\Leftrightarrow m<0\].

Ta giải gián tiếp.

Tìm m để phương trình không có nghiệm thỏa mãn \[\left| x \right|>4\].

TH1: f(x) vô nghiệm

TH2: f(x) có cả hai nghiệm thuộc khoảng [-4;4]

Như vậy f(x) không có nghiệm thỏa mãn \[\left| x \right|>4\] khi \[-\frac{25}{9}\le m<16\].

Vậy f(x) có ít nhất một nghiệm thỏa mãn \[\left| x \right|>4\] khi

Có 4 trường hợp xảy ra:

TH4: f(x) có cả hai nghiệm thuộc khoảng (-1;1).

Tóm lại :

Có 3 trường hợp:

Kết hợp các trường hợp ta được \[m\le 0\].

Câu 27:

Đặt \[t=\left| x-1 \right|\ge 0\] , thì \[{{x}^{2}}-2x={{t}^{2}}-1\].

Phương trình trở thành: \[{{t}^{2}}-mt+{{m}^{2}}-1=0\] (2).

Để (1) có nghiệm thì (2) phải có ít nhất một nghiệm \[t\ge 0\].

TH1: (2) có nghiệm t=0 \[\Leftrightarrow f(0)=0\Leftrightarrow {{m}^{2}}-1=0\Leftrightarrow m=\pm 1\].

TH2: (2) có hai nghiệm trái dấu

TH3: (2) có cả hai nghiệm dương

Kết hợp lại ta được : \[-1\le m\le \frac{2\sqrt{3}}{3}\].

Câu 28:

Phương trình đã cho là phương trình bậc hai có a = 1 ; b = 2m - 1 ; c = m - 1

Vì $\Delta >0$nên phương trình có hai nghiệm phân biệt với mọi m.

Theo định lý Viét có

Ta có $A=x_{1}^{2}\left( 1-x_{2}^{2} \right)+x_{2}^{2}\left( 1-4x_{1}^{2} \right)=x_{1}^{2}+x_{2}^{2}-5x_{1}^{2}x_{2}^{2}={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}{{x}_{2}}-5{{\left( x_{1}^{{}}x_{2}^{{}} \right)}^{2}}$ (3)

Thay (1) và (2) vào (3) ta có: