SÓNG CƠ VÀ PHƯƠNG TRUYỀN SÓNG
I. LÝ THUYẾT:
1.
Sóng cơ: là dao động cơ lan truyền trong một môi trường.
ü Lưu
ý:
· Sóng cơ không lan truyền được trong chân không.
· Khi
sóng truyền đi chỉ có các đỉnh sóng hay các vùng nén dãn (pha dao động – trạng
thái dao động) truyền đi còn các phần tử môi trường không bị truyền đi mà chỉ
dao động xung quanh VTCB của chúng.
2.
Phân loại:
a.
Sóng ngang:
-
Là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với
phương truyền sóng.
-
Sóng ngang truyền trong môi trường có biến dạng lệch: trong chất rắn và trên bề
mặt chất lỏng (sóng trên mặt nước là sóng ngang).
b.
Sóng dọc:
-
Là sóng trong đó các phần tử của môi trường dao động theo phương trùng với
phương truyền sóng.
-
Sóng dọc truyền trong môi trường có biến dạng nén – dãn: trong chất khí, chất lỏng
và chất rắn (sóng truyền trên một lò xo ống dài là sóng dọc).
3.
Các đại lượng đặc trưng của sóng:
a.
Chu kì (T) và tần số sóng (f):
- Là chu kì, tần số của phần tử môi trường có sóng truyền qua và bằng chu kì , tần số của nguồn sóng.
$T=\frac{1}{f}=\frac{2\pi
}{\omega }$ $f=\frac{1}{T}=\frac{\omega
}{2\pi }$
(ω là tần số góc của sóng)
ü Lưu
ý: Chu kì và tần số không đổi khi sóng truyền từ môi trường này sang môi trường
khác.
b.
Tốc độ truyền sóng (v):
-
Là tốc độ truyền pha dao động trong môi trường: $v=\frac{s}{t}$
-
Trong đó: s là quãng đường sóng truyền được trong thời gian t.
· Đối
với một môi trường nhất định thì tốc độ truyền sóng không đổi.
·
Tốc độ truyền sóng khác với tốc độ dao động
của các phần tử môi trường.
ü Lưu
ý: Vận tốc cực đại và gia tốc cực đại của các phần tử môi trường:
${{v}_{\max
}}=\omega A$ ${{a}_{\max
}}={{\omega }^{2}}A=\omega {{v}_{\max }}$
c.
Bước sóng ($\lambda $):
-
Bước sóng là khoảng cách giữa hai điểm sóng gần nhau nhất trên cùng một phương
truyền sóng dao động cùng pha.
-
Bước sóng là quãng đường sóng truyền được trong một chu kì.
$\lambda
=vT=\frac{v}{f}$
-
Các công thức liên hệ:
$v=\frac{\lambda }{T}=\lambda f$ $T=\frac{\lambda }{v}$ $f=\frac{v}{\lambda }$
ü Lưu
ý:
·
Khi sóng truyền từ môi trường này sang
môi trường khác thì bước sóng và tốc độ truyền sóng thay đổi.
·
Những điểm cách nhau một số nguyên lần
bước sóng ($k\lambda $) hoặc một số chẵn lần nữa bược sóng ($2k\frac{\lambda
}{2}$) trên cùng một phương truyền sóng thì dao động cùng pha.
·
Những điểm cách nhau một số bán nguyên lần
bước sóng $\left[ \left( k+\frac{1}{2} \right)\lambda\right]$ hoặc một số lẻ lần nửa bước sóng $\left[
\left( 2k+1 \right)\frac{\lambda }{2} \right]$ trên cùng một phương trên sóng
thì dao động ngược pha.
·
Khoảng cách giữa hai điểm gần nhau nhất
trên cùng một phương truyền sóng dao động cùng pha bằng bước sóng ($\lambda $).
·
Khoảng cách giữa hai điểm gần nhau nhất
trên cùng một phương truyền sóng dao động ngược pha bằng bước sóng ($\frac{\lambda
}{2}$).
· Khoảng
cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động
vuông pha bằng một phần tư bước sóng ($\frac{\lambda
}{4}$).
d.
Biên độ sóng (A):
-
Biên độ sóng tại mỗi điểm trong không gian chính là biên độ dao động của phần tử
môi trường tại điểm đó.
e.
Năng lượng sóng (W):
-
Năng lượng sóng là năng lượng dao động của các phần tử của môi trường có sóng
truyền qua.
-
Năng lượng sóng tại mỗi điểm tỉ lệ với bình phương biên độ sóng tại điểm đó.
-
Quá trình truyền sóng là quá trình truyền năng lượng.
4.
Phương trình sóng:
Tại
điểm O: ${{u}_{o}}=A\cos \omega t$
a.
Phương trình sóng tại M:
-
Biểu thức sóng tại M cách O khoảng x:
\[{{u}_{M}}=A\cos
\left[ 2\pi \left( \frac{t}{T}-\frac{x}{\lambda } \right) \right]=A\cos \left(
\omega t-\frac{2\pi x}{\lambda } \right)=A\cos \left( \omega t-\frac{\omega
x}{v} \right)\]
-
Phương trình sóng cho biết:
· Li
độ (u) của mỗi phần tử sóng theo thời gian (t) và tọa độ (x) của điểm đó.
·
Sóng có tính tuần hoàn theo thời gian với
chu kì T và theo không gian với bước sóng $\lambda $.
ü Lưu
ý 1:
·
Khoảng cách giữa n đỉnh (ngọc, gợn lồi)
sóng liên tiếp:
$L=\left( n-1
\right)\lambda $ →$\lambda =\frac{L}{n-1}$
·
Phao nhô lên cao n lần trong thời gian $\Delta
t$:
$\Delta t=\left( n-1
\right)T$→$T=\frac{\Delta t}{n-1}$
ü Lưu
ý 2:
· Nếu 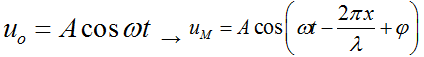
b.
Độ lệch pha giữa hai điểm cách nguồn những khoảng ${{d}_{1}}$ và ${{d}_{2}}$:
$\Delta
\varphi =\frac{2\pi }{\lambda }\left( {{d}_{1}}-{{d}_{2}} \right)=\frac{\omega
}{v}\left( {{d}_{1}}-{{d}_{2}} \right)$
ü Nếu 2 dao động cùng pha: $\Delta \varphi =2k\pi $ → ${{d}_{1}}-{{d}_{2}}=k\lambda $
ü Nếu
2 dao động ngược pha: $\Delta \varphi =\left( 2k+1 \right)\pi $ → ${{d}_{1}}-{{d}_{2}}=\left(
k+\frac{1}{2} \right)\lambda $
ü Nếu
2 điểm gần nhau nhất cùng pha: $\lambda $
ü Nếu
2 điểm gần nhau nhất ngược pha: $\frac{\lambda }{2}$
ü Nếu
2 điểm gần nhất vuông pha: $\frac{\lambda }{4}$.
II. BÀI TẬP:
Câu
1: Một nguồn phát sóng cơ dao động theo phương trình $u=4\cos
\left( 4\pi t-\frac{\pi }{4} \right)$ (cm). Biết dao động hai điểm gần nhau nhất
trên cùng một phương truyền sóng cách nhau 0,5m có độ lệch pha là . Tốc độ truyền
sóng đó:
A.
1m/s B. 2m/s C. 1,5m/s D. 6m/s
HD:
$\Delta \varphi =\frac{\pi }{3}=\frac{\omega x}{v}$ → $v=\frac{\omega x}{\Delta
\varphi }=\frac{4\pi .0,5}{\frac{\pi }{3}}=6$ m/s
Câu
2: Một sóng hình sin truyền theo phương Ox
từ nguồn O với tần số 20Hz, có tốc độ truyền sóng nằm trong khoảng từ 0,7m/s đến
1m/s. Gọi A và B là hai điểm nằm trên Ox, ở cùng một phía so với O và cách nhau
10cm. Hai phần tử môi trường tại A và B luôn dao động ngược pha với nhau. Tốc độ
truyền sóng là:
A.
100cm/s B. 80cm/s C. 85cm/s D.
90cm/s
HD:
$\Delta \varphi =\frac{2\pi d}{\lambda }=\frac{2\pi df}{v}=\left( 2k+1
\right)\pi $ → $v=\frac{4}{\left( 2k+1 \right)}$ (m/s)
Thay vào điều kiện 0,7m/s
Câu
3: Sóng cơ truyền trên một sợi dây đàn hồi
rất dài với tốc đọ là 4m/s. Hai điểm trên dây cách nhau 40cm, người ta thấy
chúng luôn dao động vuông pha. Biết tần số f có giá trị trong khoảng từ 8Hz đến
13 Hz. Tính tần số.
A.
8,5Hz B. 10Hz C. 12Hz D. 12,5Hz
HD:
$\Delta \varphi =\frac{2\pi d}{\lambda }=\frac{2\pi df}{v}=\left( 2k+1
\right)\frac{\pi }{2}$ → $f=5k+2,5$(Hz)
Thay vào điều kiện 8Hz
Câu 4: Một nguồn O phát sóng cơ dao động theo phương trình ${{u}_{o}}=2\cos \left( 20\pi t+\frac{\pi }{3} \right)$ (trong đó u tính bằng mm, t tính bằng s). Xét sóng truyền theo một đường thẳng từ O đến điểm M (M cách O một khoảng 45cm) với tốc độ 1m/s. Trong khoảng từ O đến M có bao nhiêu điểm dao động cùng pha với dao động tại nguồn O?
A. 4 B.
3 C. 2 D. 5
HD: $\Delta \varphi =\frac{2\pi d}{\lambda
}=\frac{\omega d}{v}=k2\pi $ → $d=k\frac{2\pi v}{\omega }=k\frac{2\pi .1}{20\pi
}=0,1k$ (m)
Thay vào điều kiện
0m
Câu
5: Một nguồn O phát sóng cơ dao động theo phương trình
${{u}_{o}}=2\cos \left( 20\pi t+\frac{\pi }{3} \right)$(trong đó u tính bằng mm, t tính bằng
s). Xét trên một phương truyền sóng từ O đến điểm M rồi đến điểm N với tốc đọ
1m/s. Biết OM=10cm và ON=55cm. Trong đoạn MN có bao nhiêu dao động vuông pha với
dao động tại nguồn O?
A. 10 B. 8 C. 9 D. 5
HD: Độ lệch pha của một điểm trên MN cách O một khoảng d là: $\Delta \varphi =\frac{\omega d}{v}=\frac{20\pi d}{100}=\frac{\pi d}{5}$ $$

Điểm
này dao động vuông pha với O thì $\Delta \varphi =\left( 2k+1 \right)\frac{\pi
}{2}$ → $d=5k+2,5$ (cm).
Thay
vào điều kiện OM≤d≤ON
→
10≤5k+2,5≤55 → 1,5≤k≤10,5 → k=2; 3; 4; 5; 6; 7; 8; 9; 10 → Có 9 giá trị.
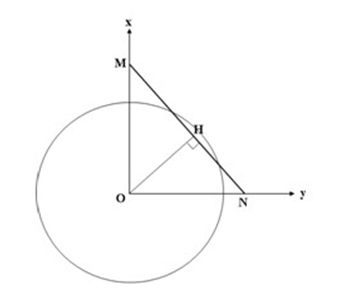
Chú
ý: Trường hợp O, M, N không thẳng hàng
Từ
O kẻ đường thẳng vuông góc với MN cắt tại H, chia MN thàng hai đoạn MH và HN,
tìm số điểm trên từng đoạn rồi cộng lại dựa vào điều kiện
OH≤d≤OM
OH<><>
III. TRẮC NGHIỆM:
Câu
1: Sóng cơ lan truyền trên sợi dây, qua hai điểm M và
N cách nhau 150cm và M sớm pha hơn N là $\frac{\pi }{3}+k\pi $(k là số nguyên).
Từ M đến N chỉ có 3 điểm vuông pha với M. Biết tần số f=10Hz. TÍnh tốc độ truyền
sóng trên dây.
A.
100cm/s B. 800cm/s C. 900cm/s D. 80cm/s
HD:
Vì chỉ có 3 điểm vuông pha với M nên: $\frac{5\pi }{2}\le \Delta \varphi \le
\frac{7\pi }{2}$ hay $\frac{5\pi }{2}\le \frac{\pi }{3}+k\pi \le \frac{7\pi
}{2}$→ 2,2≤k≤3,2 → k=3
$\Delta
\varphi =\frac{2\pi d}{\lambda }=\frac{2\pi df}{v}=\frac{20\pi
.150}{v}=\frac{\pi }{3}+3\pi $ → v=900cm/s
Câu
2: Sóng truyền với tốc độ 6m/s từ điểm O đếm điểm M nằm
trên cùng một phương truyền sóng cách nhau 3,4m. Coi biên đọi sóng không đổi.
Viết phương trình sóng tại M, biết phương trình sóng tại O${{u}_{o}}=5\cos
\left( 5\pi t+\frac{\pi }{6} \right)$
A.${{u}_{o}}=5\cos \left( 5\pi t-\frac{17\pi }{6} \right)$ B. ${{u}_{o}}=5\cos \left( 5\pi t-\frac{8\pi }{3} \right)$
C.${{u}_{o}}=5\cos \left( 5\pi t+\frac{4\pi }{3} \right)$ D.${{u}_{o}}=5\cos \left( 5\pi t-\frac{2\pi }{3} \right)$
HD: Dao động tại M trễ pha hơn dao động tại O là:
$\Delta \varphi =\frac{2\pi
d}{\lambda }=\frac{2\pi d}{vT}=\frac{\omega d}{v}=\frac{5\pi
.3,4}{6}=\frac{17\pi }{6}$ → ${{u}_{M}}=5\cos \left( 5\pi t+\frac{\pi
}{6}-\frac{17\pi }{6} \right)=5\cos \left( 5\pi t-\frac{8\pi }{3} \right)$
Câu 3: Tạo sóng ngang trên một dây đàn hồi Ox. Một điểm
M cách nguồn phát sóng tại O một khoảng d=50cm có phương trình dao động ${{u}_{M}}=2\cos
0,5\pi \left( t-\frac{1}{20} \right)$, tốc độ truyền sóng trên dây là 10m/s.
Phương trình dao động tại nguồn O.
A.${{u}_{o}}=2\cos 0,5\pi \left( t-0,1 \right)$ B. ${{u}_{o}}=2\cos 0,5\pi t$
C.${{u}_{o}}=2\cos \left( 5\pi t \right)$ D.${{u}_{o}}=2\cos \left( 5\pi t-\frac{2\pi }{3} \right)$
HD: (tương tự câu trên).
Câu 4: Sóng trên với tốc độ 5m/s giữa hai điểm O và M
nằm trên cùng một phương trình sóng. Biết phương trình sóng tại O là ${{u}_{o}}=5\cos
\left( 5\pi t+\frac{\pi }{3} \right)$. Xác định khoảng cách OM và cho biết chiều
truyền sóng:
A. Truyền từ O đến M,
OM=0,5m.
B. Truyền từ M đến O, OM=0,5m.
C. Truyền từ O đến M,
OM=0,25m.
D. Truyền từ M đến O,
OM=0,25m.
HD: Dao động tại M sớm hơn tại O là $\Delta
\varphi =\frac{\pi }{2}$ nên sóng truyền từ M đến O và $\Delta \varphi
=\frac{\omega d}{v}$ → d=0,5m
Câu 5: Một sóng cơ học lan truyền dọc theo một đường
thẳng với biên độ không đổi, phương trình sóng tại nguồn O là $u=A\cos \left(
\frac{2\pi t}{T} \right)$ . Một điểm M cách nguồn O bằng 7/6 lần bước sóng ở thời
điểm t=1,5T có li độ -3cm. Biên độ sóng tại A là:
A. 6cm B.
5cm C. 4cm D. 7cm
HD: Dao động tại M trễ pha hơn dao động tại O là: $\Delta
\varphi =\frac{2\pi d}{\lambda }=\frac{7\pi }{3}$
→ ${{u}_{M}}=A\cos \left(
\frac{2\pi t}{T}-\frac{7\pi }{3} \right)$ → ${{u}_{M\left( 1,5T \right)}}=A\cos
\left( \frac{2\pi t}{T}1,5T-\frac{7\pi }{3} \right)=-3$→ A=6cm
Câu 6: Sóng cơ truyền trong một môi trường dọc theo
trục Ox với phương trình $u=\cos \left( 20t-4x \right)$ . Vận tốc truyền sóng
này trong môi trường trên bằng:
A. 5m/s B.
50cm/s C. 40cm/s D. 4m/s
HD:
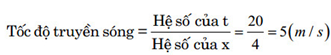
Câu 7: Một sóng có học truyền theo phương Ox với
biên độ không đổi. Phương trình dao động tại nguồn O có dạng $u=6\sin \left(
\frac{\pi t}{3} \right)$ .Tại thời điểm ${{t}_{1}}$ li độ của điểm O là 3cm. Vận
tốc dao động tại O sau thời điểm đó 1,5s là
A. $-\frac{\pi }{3}$ cm/s B. $-\pi $ cm/s C. $\pi $ cm/s D. $\frac{\pi }{3}$ cm/s
HD:
$T=\frac{2\pi }{\omega }=6$→$\frac{T}{4}=1,5$→${{t}_{2}}-{{t}_{2}}=\left( 2,0+1 \right)\frac{T}{4}$→${{v}_{2}}=-\omega
{{u}_{1}}=-\frac{\pi }{3}.3=-\pi $ (cm/s)
Câu 8: Nguồn sóng ở O dao động với tần số 10Hz, dao động
truyền đi với vận tốc 0,4m/s trên phương Oy. Trên phương này có 2 điểm P và Q theo
thứ tự đó PQ=15cm. Cho biên độ A=4cm và biên độ không thay đổi khi truyền sóng.
Nếu tại thời điểm nào đó P có li độ 3cm thì vận tốc dao động tại Q là:
A. +60π cm/s B.
-60π cm/s C. +20π cm/s D. -20π cm/s
HD:
$\Delta \varphi =\frac{2\pi
d}{\lambda }=\frac{2\pi df}{v}=7\pi +\frac{\pi }{2}=\left( 2.7+1
\right)\frac{\pi }{2}$
Vì n=7 là số lẻ nên ${{v}_{Q}}=+\omega
{{u}_{P}}=+60\pi $ cm/s
Câu 9: Một nguồn phát sóng cơ dao động với phương
trình $u=4\cos \left( 4\pi t-\frac{\pi }{4} \right)$ . Biết dao động tại hai điểm
gần nhau nhất trên cùng một phương truyền sóng cách nhau 0,5m có độ lệch pha là
. Tình tốc độ truyền sóng:
A. 5m/s B. 6m/s C. 8m/s D.
12m/s
Câu 10: Một sóng cơ truyền trong môi trường đàn hồi.
Phương trình dao động của nguồn O có dạng $u=4\cos \left( \frac{\pi }{3}t
\right)$. Tính độ lệch phâ của dao động tại một điểm M bất kì sau khoảng thời
gian 0,5s
A.$\frac{\pi }{6}$ B. $\frac{\pi
}{3}$ C. $\frac{\pi }{4}$ D. $\frac{\pi }{2}$
HD: $\omega
=\frac{\pi }{3}$ → độ lệch pha của điểm M là: $\Delta \varphi =\omega .\Delta
t=\frac{\pi }{6}$







