CÁC DẠNG TOÁN CĂN BẬC HAI SỐ HỌC TRONG CHƯƠNG TRÌNH SÁCH GIÁO KHOA LỚP 9
Bài 1: Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng 121; 144; 169; 225; 256; 324; 361; 400.
Hướng dẫn giải:
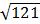 =11. Hai căn bậc hai của 121 là 11 và -11.
=11. Hai căn bậc hai của 121 là 11 và -11.
 =12. Hai căn bậc hai của 144 là 12 và -12.
=12. Hai căn bậc hai của 144 là 12 và -12.
 =13. Hai căn bậc hai của 169 là 13 và -13.
=13. Hai căn bậc hai của 169 là 13 và -13.
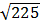 =15. Hai căn bậc hai của 225 là 15 và -15.
=15. Hai căn bậc hai của 225 là 15 và -15.
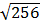 =16. Hai căn bậc hai của 256 là 16 và -16.
=16. Hai căn bậc hai của 256 là 16 và -16.
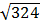 = 18. Hai căn bậc hai của 324 là 18 và -18.
= 18. Hai căn bậc hai của 324 là 18 và -18.
 = 19. Hai căn bậc hai của 361 là 19 và -19.
= 19. Hai căn bậc hai của 361 là 19 và -19.
 = 20. Hai căn bậc hai của 400 là 20 và -20.
= 20. Hai căn bậc hai của 400 là 20 và -20.
Bài 2: So sánh hai căn bậc 2
a) 2 và 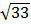 ; b) 6 và
; b) 6 và 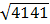 ; c) 7 và =
; c) 7 và =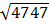
Lời giải:
a) Ta có: 2 =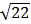 =
=  = 22 = 4 và 4 > 34 > 3 nên ta suy ra
= 22 = 4 và 4 > 34 > 3 nên ta suy ra  >
> 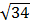 > 3
> 3
Vậy 2 >  > 3.
> 3.
b) Ta có 6 =  = 36 và 36 < 41 nên ta suy ra 36 < 41
= 36 và 36 < 41 nên ta suy ra 36 < 41
Vậy 6 <  < 41.
< 41.
c) Tương tự như hai câu trên, ta cũng viết lại là:
7 = 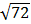 =
= 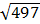 = 49 và 49 > 47nên ta suy ra
= 49 và 49 > 47nên ta suy ra  >
> 
Vậy 7 >  > 47
> 47
Bài 3: Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau ( làm tròn đến chữ số thập phân thứ 3)
1. a) x2 = 2 ; b) x2 = 3
2. c) x2 = 3,5; d) x2 = 4,12
Hướng dẫn giải:
Nghiệm của phương trình x2 = a ( với a 0) là căn bậc hai của a.
0) là căn bậc hai của a.
1. a) x2 = 2 ⟺ x =
x = 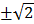 x2 = 2
x2 = 2 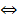 x =
x = 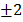
Tính bằng máy tính ta được: x 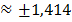
b) x2 = 3 
tính bằng máy tính ta được: x≈±1,732
2. c) x2 = 3,5 ⟺x=± 3,5 x2 = 3,5 ⟺x= ±3,5
Tính bằng máy tính ta được:
x ≈±1,871
d) x2 = 4,12 
Tính bằng máy tính ta được:
x≈±2,03
Bài 4: Tìm số x không âm, biết:
1. a) 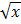 =15x = 15; b) 2x = 142x =14
=15x = 15; b) 2x = 142x =14
2. c)  <
< 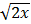 < 2; d)
< 2; d) 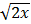 < 42x < 4.
< 42x < 4.
Hướng dẫn giải:
a) Vận dụng điều lưu ý trong phần tóm tắt kiến thức bài học:
“ Nếu a ≥0 thì a = (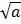 )2a = (a)2”
)2a = (a)2”
.png)
.png)
c) Là một bất phương trình của hai số không âm, ta sẽ bình phương cả hai vế:
\[\sqrt{x}<\sqrt{2}\Leftrightarrow {{\left( \sqrt{x} \right)}^{2}}={{\left( \sqrt{2} \right)}^{2}}\Leftrightarrow x<4x<2\Leftrightarrow {{\left( x \right)}^{2}}<\left( 2 \right)\Leftrightarrow x<4\]
d) Là một bất phương trình của hai số không âm, ta sẽ bình phương cả hai vế:
\[\sqrt{2x}<4\Leftrightarrow {{\left( \sqrt{2x} \right)}^{2}}<{{4}^{2}}\Leftrightarrow 2x<16\Leftrightarrow x<8\]
Bài 5: Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của một hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
Hướng dẫn giải:
Gọi x là độ dài hình vuông, x > 0.
Diện tích của hình vuông là x2.
Diện tích của hình chữ nhật là 3,5.14 =49 (m2)
Theo đề bài, diện tích hình vuông = diện tích hình chữ nhật = 49
Cạnh của hình vuông bằng \[\sqrt{49}=\pm 7(m)\]. Vì x > 0 nên x = 7.
Vậy độ dài cạnh hình vuông là 7m.







