KIẾN THỨC CƠ BẢN VỀ ĐỘ DÀI ĐƯỜNG TRÒN, CUNG TRÒN
Trong chương trình toán lớp 9 cơ bản có các bài toán thuộc lý thuyết về độ dài đường tròn , cung tròn bao gồm:
1. Công thức tính độ dài đường tròn, cung tròn.
Độ dài CC của một đường tròn có bán kính RR được tính theo công thức:
\[C=2\pi RC=2\pi R\]
Nếu gọi d là đường kính đường tròn \[\left( d=2R \right)\] thì:
\[C=\pi dC=\pi d\]
2. Cách tính độ dài đường tròn
Trên đường tròn bán kính RR, độ dài II của một cung \[n\circ \]được tính theo công thức:
\[II=\pi Rn\circ 180\circ \]
Dưới đây là một số dạng toán hình học lớp 9 cơ bạn mà bạn có thể gặp trong chương trình sách giáo khoa.
Bài 1: Cho tam giác ABC, đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Bài giải:
.png)
a) Gọi O là trung điểm của BC.
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
\[EO=\frac{1}{2}BC\]; \[DO=\frac{1}{2}BC\].
Suy ra \[OE=OD=OB=OC\left( =\frac{1}{2}BC \right)\].
Do đó 4 điểm B, E, D, C cùng thuộc đường tròn \[\left( O \right)\]đường kính BC.
b) Xét đường \[\left( O;\frac{BC}{2} \right)\], BC là đường kính, DE là một dây cung không đi qua tâm, do đó DE < BC.
Bài 2: Cho đường tròn \[\left( O \right)\] đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Bài giải:
.png)
Vẽ OM  CD
CD
Xét tam giác OCD có:
.png)
Tam giác OCD cân tại O có OM là đường cao nên cũng đồng thời là đường trung tuyến.
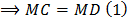
Xét hình thang AHKB, ta có:
OM ∕∕ AH ∕∕BK ( cùng vuông góc với CD)
\[AO=BO=\frac{AB}{2}\]
Vậy MO là đường trung bình của hình thang AHKB
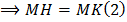
Từ (1) và (2) ⇒CH=DK
Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.
Bài 3: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng mình rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
.png)
Bài giải:
Gọi O là giao điểm hai đường chéo của hình chữ nhật, ta có OA = OB =OC = OD = R.
Bốn điểm A, B, C, D cách đều điểm O nên bốn điểm này cùng thuộc một đường tròn.
Xét tam giác ABC vuông tại B, có:
\[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}={{12}^{2}}+{{5}^{2}}=169\Rightarrow AC=13.\]
Bán kính của đường tròn là \[R=\frac{13}{2}=6,5\].
Nhận xét: Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.
Bài 4: Chứng mình các định lý sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Hướng dẫn giải :
.png)
a) Xét tam giác ABC vuông tại A.
Gọi O là trung điểm của cạnh huyền BC, ta có:
OA = OB = OC =R .
Vậy O chính là tâm của đường tròn ngoại tiếp tam giác ABC.
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC.
.png)
Ta có OA = OB =OC = R
Suy ra \[OA=\frac{1}{2}BC\], dó đó tam giác ABC vuông tại A.
Nhận xét: Định lý trong bài tập này thường được dùng để giải nhiều bài tập về nhận biết tam giác vuông.







