GIAO THOA SÓNG

CHUYÊN ĐỀ GIAO THOA SÓNG

A, TÓM TẮT KIẾN THỨC

1, Định nghĩa: là sự tổng hợp của hai sóng kết hợp trong không gian, trong đó có những chỗ biên độ sóng được tăng cường hay bị giảm bớt.

2, Nguồn sóng kết hợp, sóng kết hợp

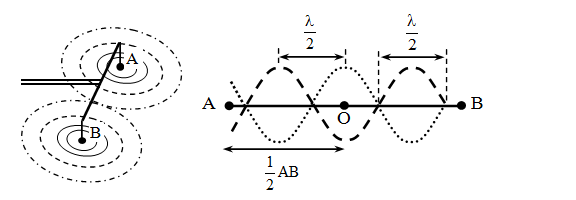
a) Nguồn kết hợp

- Hai nguồn giao động cùng tần số và có độ lệch pha không đổi ( theo thời gian ) gọi là 2 nguồn kết hợp

b) Sóng kết hợp

- Hai sóng do hai nguồn kết hợp tạo ra gọi là hai sóng kết hợp

3, Định nghĩa giao thoa sóng

- Là sự kết hợp của 2 hai nhiều  sóng kết hợp trong không gian đó có những điểm cố định mà biên độ sóng được tang cường nhau ( Cực đại giao thoa) hoặc giảm bớt nhau ( cực tiểu giao thoa)

4, Điều kiện xảy ra giao thoa sóng

- Hai sóng gặp nhau phải là hai sóng kết hợp và dao động cùng phương

5, Lý thuyết về giao thoa

- Khảo sát giao thoa sóng trên mặt nước

Giả sử 2 nguồn kết hợp cùng pha, có phương trình:

${{u}_{1}}={{u}_{2}}=A.\cos (\omega t+\varphi )$

Phương trình sóng tại M do ${{S}_{1}}$ và từ ${{S}_{2}}$ truyền đến

${{u}_{1M}}=A.\cos (\omega t+\varphi -\frac{2\pi .{{d}_{1}}}{\lambda })$

${{u}_{2M}}=A.\cos (\omega t+\varphi -\frac{2\pi .{{d}_{2}}}{\lambda })$

Phương trình sóng tổng hợp

$\Leftrightarrow u=2A.\cos \frac{\pi }{\lambda }({{d}_{2}}-{{d}_{1}}).\cos (\omega t+\varphi -\frac{\pi }{\lambda }({{d}_{2}}+{{d}_{1}})$

Biên độ sóng tổng hợp

${{A}_{th}}=2.A.\left| \cos \frac{\pi }{\lambda }({{d}_{2}}-{{d}_{1}}) \right|$

Vị trí cực đại giao thoa ${{A}_{\max }}=2A$

$\Leftrightarrow \cos \frac{\pi }{\lambda }({{d}_{2}}-{{d}_{1}})=\pm 1=\cos k\pi $

$\Leftrightarrow {{d}_{2}}-{{d}_{1}}=k\lambda $ ($k\in Z$ )

b) Vị trí cực tiểu giao thoa ${{A}_{\min }}=0$

$\Leftrightarrow \cos \frac{\pi }{\lambda }({{d}_{2}}-{{d}_{1}})=0=\cos (2k'+1)\frac{\pi }{2}$

$\Leftrightarrow {{d}_{2}}-{{d}_{1}}=(2k'+1)\frac{\lambda }{2}$

$\Leftrightarrow {{d}_{2}}-{{d}_{1}}=(k'+\frac{1}{2})\lambda $

Đường trung trực của ${{S}_{1}}{{S}_{2}}$ là đường cực đại giao thoa (k=0)

6, Ý nghĩa của hiện tượng giao thoa

- Hiện tượng giao thoa là hiện tượng đặc trung cho quá trình sóng

* Chú ý

a) Trên đoạn thẳng ${{S}_{1}}{{S}_{2}}$ khoảng cách giữa 2 điểm cực đại hoặc cực tiểu giao thoa kế tiếp là $\frac{\lambda }{2}$

b) Nếu 2 nguồn kết hợp có độ lớn lệch pha bất kì

Phương trình sóng tại M

$u=2A.\cos (\frac{\pi }{\lambda }({{d}_{2}}-{{d}_{1}})-\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{2}).\cos (\omega t-\frac{\pi }{\lambda }({{d}_{2}}+{{d}_{1}})+\frac{{{\varphi }_{2}}+{{\varphi }_{1}}}{2})$

+) Vị trí cực đại giao thoa: ${{d}_{2}}-{{d}_{1}}=(k+\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{2\pi }).\lambda $

+) Vị trí cực tiểu giao thoa: ${{d}_{2}}-{{d}_{1}}=(k+\frac{1}{2}+\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{2\pi }).\lambda $

c) Nếu hai nuồn kết hợp ngược pha

Cực đại giao thoa: ${{d}_{2}}-{{d}_{1}}=(k+\frac{1}{2}).\lambda $

Cực tiểu giao thoa: ${{d}_{2}}-{{d}_{1}}=k.\lambda $

B, BÀI TẬP MẪU

Câu 1: Trên mặt nước có hai nguồn phát sóng kết hợp A, B có cùng biên độ a = 2 cm, cùng tần số f = 20 Hz, ngược pha nhau. Coi biên độ sóng không đổi, vận tốc sóng v = 80 cm/s. Biên độ dao động tổng hợp tại điểm M có AM = 12 cm, BM = 10 cm là: 

    A. 4 cm                     B. 2 cm.                      C.\[\text{2}\sqrt{\text{2}}\]cm.                     D. 0 cm.

Hướng dẫn giải:

Ta có $\text{ }\!\!\lambda\!\!\text{ }=\frac{\text{v}}{\text{f}}=\text{ 4 cm}$, AM – BM = 2cm = $(k+\frac{1}{2})\lambda $ (với k = 0)

Hai nguồn ngược pha nên điểm M dao động cực đại Þ Biên độ dao động tổng hợp tại M: a = 4 cm.

Câu 2: Cho hai nguồn kết hợp A, B dao động với phương trình u_A = u_B = 2.cos(10πt) cm. Tốc độ truyền sóng là v = 3 m/s.

a) Viết phương trình sóng tại M cách A, B một khoảng lần lượt d₁ = 15 cm; d₂ = 20 cm.

b) Tính biên độ và pha ban đầu của sóng tại N cách A và B lần lượt 45 cm và 60 cm.

Hướng dẫn

a) Từ phương trình ta có ƒ = 5 Hz bước sóng λ = v/ƒ = 300/5 = 60 cm.

          Phương trình sóng tại M do các nguồn truyền đến là

Phương trình dao động tổng hợp tại M là:

\[{{u}_{M}}=\text{ }{{u}_{AM}}+\text{ }{{u}_{BM}}\] = 2cos(10πt-\[\frac{2\pi {{d}_{1}}}{\lambda }\]) + 2cos(ωt -\[\frac{2\pi {{d}_{2}}}{\lambda }\]) = 4cos\[\left( \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right)\]cos\[\left( 10\pi t-\frac{\pi \left( {{d}_{2}}+{{d}_{1}} \right)}{\lambda } \right)\]

    Thay các giá trị của d₁ = 15 cm; d₂ = 20 cm, λ = 60 cm vào ta được

u_M = 4cos\[\frac{\pi }{12}\]cos\[\left( 10\pi t-\frac{7\pi }{12} \right)\] cm

b) Áp dụng công thức tính biên độ và pha ban đầu ta được

    A_N = \[\left| 2a\cos \left( \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right) \right|\]= \[\left| 4\cos \left( \frac{\pi \left( 60-15 \right)}{60} \right) \right|\]= 2\[\sqrt{2}\] cm

    Pha ban đầu tại N là φ_N = \[-\frac{\pi \left( {{d}_{2}}+{{d}_{1}} \right)}{\lambda }=-\frac{\pi \left( 60+40 \right)}{60}\] = - \[\frac{-7\pi }{4}\]

Câu 3: Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp S₁ và S₂ cách nhau 10 cm dao động cùng pha và có bước sóng 2 cm. Coi biên độ sóng không đổi khi truyền đi.

  a. Tìm số điểm dao động với biên độ cực đại, số điểm dao động với biên độ cực tiểu quan sát được.

  b. Tìm vị trí các điểm dao động với biên độ cực đại  trên đoạn S₁S₂.

Hướng dẫn giải :

Vì các nguồn dao động cùng pha.

 a. Ta có số đường hoặc số điểm dao động cực đại:

$-\frac{l}{\text{ }\!\!\lambda\!\!\text{ }}<\text{k}<\frac{l}{\text{ }\!\!\lambda\!\!\text{ }}$ => $-\frac{10}{2}<\text{k}<\frac{10}{2}$ => – 5< k < 5. Suy ra: k = 0; ± 1;±2 ;±3; ±4.

Vậy có 9 số điểm (đường) dao động cực đại.

Ta có số đường hoặc số điểm dao động cực tiểu:

   => – 5,5< k < 4,5.

Suy ra: k = 0; ± 1;±2 ;±3; ±4; - 5.

Vậy có 10 số điểm (đường) dao động cực tiểu.      

b. Tìm vị trí các điểm dao động với biên độ cực đại  trên đoạn S₁S₂.

Ta có:  \[{{d}_{1}}+\text{ }{{d}_{2}}=\text{ }{{S}_{1}}{{S}_{2~~~~~~~~~~~~~~~~~}}~\] (1) 

   \[{{d}_{1}}\text{ }{{d}_{2}}~=\text{ }{{S}_{1}}{{S}_{2}}\]            (2)

Suy ra: \[{{d}_{1}}\] = $\frac{{{\text{S}}_{\text{1}}}{{\text{S}}_{\text{2}}}}{\text{2}}+\frac{\text{k }\!\!\lambda\!\!\text{ }}{\text{2}}$=$\frac{10}{2}+\frac{\text{k}2}{2}$ = 5+ k với  \[k\text{ }=\text{ }0;\pm 1;\pm 2\text{ };\pm 3;\pm 4.\]

Vậy có 9 điểm dao động với biên độ cực đại  trên đoạn\[{{S}_{1}}{{S}_{2}}\] .

Khoảng cách giữa 2 điểm dao động cực đại liên tiếp bằng $\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{2}}$ = 1 cm.

Câu 4: Hai nguồn sóng cơ S₁ và S₂ trên mặt chất lỏng cách nhau 20 cm dao động theo phương trình \[{{\text{u}}_{\text{1}}}={{\text{u}}_{\text{2}}}=4\cos \text{40 }\!\!\pi\!\!\text{ t}\] (cm, s), lan truyền trong môi trường với tốc độ v = 1,2 m/s.

1.  Xét các điểm trên đoạn thẳng nối S₁ với S₂.

     a. Tính khoảng cách giữa hai điểm liên tiếp có biên độ cực đại.

     b. Trên S₁S₂ có bao nhiêu điểm dao động với biên độ cực đại.

2.  Xét điểm M cách S₁ khoảng 12 cm và cách S₂ khoảng 16 cm. Xác định số đường cực đại đi qua  S₂M.

Hướng dẫn giải :

1a.  Khoảng cách giữa hai điểm liên tiếp có biên độ cực đại:  $\lambda $ = vT = \[v\frac{\text{2}\pi }{\omega }\]= 6 cm.

Hai nguồn này là hai nguồn kết hợp (và cùng pha) nên trên mặt chất lỏng sẽ có hiện tượng giao thoa nên các điểm dao động cực đại trên đoạn  l = S₁S₂ = 20 cm  sẽ có:  $\Rightarrow $ \[{{\text{d}}_{\text{1}}}=\frac{1}{2}\text{k }\!\!\lambda\!\!\text{ }+\frac{1}{2}l\]. 

Khoảng cách giữa hai điểm liên tiếp cực đại thứ k và thứ (k + 1) là : \[\Delta \text{d}={{\text{d}}_{1(\text{k}+1)}}-{{\text{d}}_{\text{1k}}}=\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{2}}\]= 3 cm.

Trên đoạn thẳng nối 2 nguồn, khoảng cách giữa hai cực đại liên tiếp bằng \[\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{2}}\].

1b. Số điểm dao động với biên độ cực đại trên S₁S₂ :

Do các điểm dao động cực đại trên S₁S₂ luôn có :

 \[-3,33<\text{k}<3,33\] \[\to \] có 7 điểm dao động cực đại.

2. Số đường cực đại đi qua đoạn S₂M

Giả thiết tại M là một vân cực đại, ta có:

 \[{{\text{d}}_{2}}-{{d}_{1}}=k\lambda \to k=\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }=\frac{16-12}{6}\approx 0,667\]

=> M không phải là vân cực đại mà M nằm trong khoảng vân cực đại số 0 và vân cực đại số 1 => trên  S₂M chỉ có 4 cực đại.

Câu 5: Âm thoa có tần số f = 100 Hz tạo ra trên mặt nước hai nguồn dao động O₁ và O₂ dao động cùng pha cùng tần số. Biết trên mặt nước xuất hiện một hệ gợn lồi gồm một gợn thẳng và 14 gợn dạng hypebol mỗi bên. Khoảng cách giữa 2 gợn ngoài cùng đo được là 2,8 cm.

     a. Tính vận tốc truyền sóng trên mặt nước. 

     b. Xác định trạng thái dao động của hai điểm M₁ và M₂ trên mặt nước. Biết O₁M₁ = 4,5 cm; O₂M₁ = 3,5 cm và O₁M₂ = 4 cm; O₂M₂ = 3,5 cm.

Hướng dẫn

a. Tính vận tốc truyền sóng trên mặt nước 

Theo đề mỗi  bên 7 gợn ta có 14. $\frac{\text{ }\!\!\lambda\!\!\text{ }}{2}$= 2,8

Suy ra \[\lambda \] = 0,4cm.

Vận tốc v = \[\lambda \]f  = 0,4.100 = 40 cm/s.

b. Xác định trạng thái dao động của hai điểm M₁ và M₂.

Dùng công thức hiệu đường đi của sóng từ hai nguồn đến M₁ là:

\[{{d}_{1}}-{{d}_{2}}=(\Delta {{\varphi }_{M1}}-\Delta \varphi )\frac{\lambda }{2\pi }\]     

Với 2 nguồn cùng pha nên \[\Delta \varphi \] = 0, suy ra:

        \[{{d}_{1}}-{{d}_{2}}=\frac{\lambda }{2\pi }\Delta {{\varphi }_{M1}}=>\Delta {{\varphi }_{M1}}=({{d}_{1}}-{{d}_{2}})\frac{2\pi }{\lambda }\].

Thế số : \[\text{ }\!\!\Delta\!\!\text{ }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{M}}}=(4,5-3,5)\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{0,4}}\]=5$\pi $ = (2k + 1) $\pi $ , dao động thành phần ngược pha nên tại M₁  có trạng thái dao động cực tiểu (biên độ cực tiểu).

Tương tự  tại M₂:  \[{{d}_{1}}-{{d}_{2}}=\frac{\lambda }{2\pi }\Delta {{\varphi }_{M2}}=>\Delta {{\varphi }_{M2}}=({{d}_{1}}-{{d}_{2}})\frac{2\pi }{\lambda }\].

Thế số : \[\Delta {{\varphi }_{M}}=(4-3,5)\frac{2\pi }{0,4}=0,5.\frac{2\pi }{0,4}=2,5\pi =(2k+1)\frac{\pi }{2}\] => hai dao động thành phần vuông pha nên tại M₂  có biên độ dao động A sao cho \[{{\text{A}}^{2}}=\text{A}_{1}^{2}+\text{A}_{2}^{2}\]  với A₁ và A₂ là biên độ của 2 hai động thành phần tại M₂ do 2 nguồn truyền tới.

C, BÀI TẬP TỰ LUYỆN           

1. Trên mặt nước có hai nguồn sóng nước giống nhau A và B dao động cùng pha, cách nhau một khoảng AB = 12 cm. C là một điểm trên mặt nước, cách đều hai nguồn và cách trung điểm O của đoạn AB một khoảng CO = 8 cm. Biết bước sóng \[\lambda \] = 1,6 cm. Số điểm dao động ngược pha với nguồn có trên đoạn CO là: A. 4.                B. 5. C. 2. D. 3.

2. Hai nguồn kết hợp \[{{S}_{1}}v\grave{a}\text{ }{{S}_{2}}\] cách nhau một khoảng là 11 cm đều dao động theo phương trình \[u\text{ }=\text{ }acos\left( 20\pi t \right)\] mm trên mặt nước. Biết tốc độ truyền sóng trên mặt nước 0,4 m/s và biên độ sóng không đổi khi truyền đi. Hỏi điểm gần nhất dao động ngược pha với các nguồn nằm trên đường trung trực của \[{{S}_{1}}{{S}_{2}}\] cách nguồn \[{{S}_{1}}\] bao nhiêu?        A. 32 cm.   B. 18 cm.    C. 24 cm.                           D. 6 cm.

3. Hai nguồn kết hợp \[{{S}_{1}},\text{ }{{S}_{2}}\] cách nhau một khoảng là 50 mm đều dao động theo phương trình \[u\text{ }=\text{ }asin\left( 200\pi t \right)\] mm trên mặt nước. Biết vận tốc truyền sóng trên mặt nước v = 0,8 m/s và biên độ sóng không đổi khi truyền đi. Hỏi điểm gần nhất dao động cùng pha với nguồn trên đường trung trực của \[{{S}_{1}}{{S}_{2}}\] cách nguồn \[{{S}_{1}}\] bao nhiêu?

   A. 32 mm.                 B. 28 mm.                 C. 24 mm.                 D. 12 mm.

4. Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12 cm đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng \[\lambda \] = 1,6 cm. C và D là hai điểm khác nhau trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8 cm. Số điểm dao động cùng pha với nguồn ở trên đoạn CD là: A. 3.   B. 10.         C. 5.        D.6

5. Dùng một âm thoa có tần số rung ƒ = 100 Hz người ta tạo ra tại hai điểm S₁, S₂ trên mặt nước hai nguồn sóng cùng biên độ, cùng pha. Biết \[{{S}_{1}}{{S}_{2}}\] = 3,2 cm, tốc độ truyền sóng là v = 40 cm/s. Gọi I là trung điểm của \[{{S}_{1}}{{S}_{2}}\]. Tính khoảng cách từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực \[{{S}_{1}}{{S}_{2}}\] là:                       

A. 1,8 cm.                     B. 1,3 cm.                 C. 1,2 cm.                 D. 1,1 cm.

6. Có 2 nguồn sóng kết hợp \[{{S}_{1}}v\grave{a}\text{ }{{S}_{2}}\] dao động cùng biên độ, cùng pha và \[{{S}_{1}}{{S}_{2}}\] = 2,1 cm. Khoảng cách giữa 2 cực đại ngoài cùng trên đoạn \[{{S}_{1}}{{S}_{2}}\] là 2 cm. Biết tần số sóng ƒ = 100 Hz. Tốc độ truyền sóng là v = 20 cm/s. Trên mặt nước quan sát được số đường cực đại mỗi bên của đường trung trực \[{{S}_{1}}{{S}_{2}}\] là

   A. 10.                        B. 20.                        C. 40.                        D. 5.

7. Trong thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A và B dao động với phương trình lần lượt là \[{{u}_{A}}=\text{ }{{u}_{B}}=\text{ }4cos\left( 20\pi t \right),\] tốc độ truyền sóng trên mặt nước là 30 cm/s, coi biên độ sóng là không đổi. Tại điểm M nằm trên AB, cách trung điểm O của AB là 3,75 cm thì dao động với biên độ: 

A. 8 cm.                        B. 4 cm.                    C. 0 cm.                    D. 6 cm.

8. Một nguồn O phát sóng cơ dao động theo phương trình \[{{u}_{O}}=\text{ }2cos\left( 20\pi t\text{ }+\text{ }\pi /3 \right)\] (Trong đó u tính bằng đơn vị mm, t tính bằng đơn vị s). Xét sóng truyền theo một đường thẳng từ O đến điểm M với tốc độ không đổi 1 m/s. Trong khoảng từ O đến M có bao nhiêu điểm dao động cùng pha với dao động tại nguồn O? Biết M cách O một khoảng 45 cm:

 A. 4.      B. 3.        C. 2.                               D. 5.

9. tại hai điểm S₁S₂ trên mặt nước tạo ra sóng kết hợp có biểu thức\[{{u}_{1}}=\text{ }{{u}_{2}}=\text{ }Acos\left( \omega t \right)\] . Sóng do hai nguồn tạo ra trên mặt nước có bước sóng λ. khoảng cách giữa hai điểm \[{{S}_{1}}{{S}_{2}}\] bằng 13\[\lambda \] . Điểm M nằm trên đường trung trực S₁S₂ dao động cùng pha với hai nguồn kết hợp \[{{S}_{1}}{{S}_{2}}\] cách trung điểm của \[{{S}_{1}}{{S}_{2}}\] một đoạn nhỏ xấp xỉ bằng:  

A. 3,6\[\lambda \].         B. 5,5\[\lambda \].     C. 2,6\[\lambda \].     D. 4,5\[\lambda \].

10. Trong thí nghiệm dao thoa sóng trên mặt nước, hai nguồn A,B dao động cùng ha với tần số ƒ = 40 Hz cách nhau 25 cm, vận tốc truyền sóng là v = 60 cm/s. Một điểm M nằm trên đường trung trực của AB cách trung điểm I của AB 16 cm. Trên đoạn IM có bao nhiêu điểm giao động cùng pha với nguồn.

   A. 4.                                                            B. 3.                          C. 6. D. 5.

11. Trên mặt nước có 2 nguồn sóng ngang cùng tần số 25 Hz, cùng pha và cách nhau 32 cm. Tốc độ truyền sóng là 30cm/s. M là điểm trên mặt nước cách đều 2 nguồn sóng và cách N một khoảng 12 cm(với N là trung điểm đoạn thẳng nối hai nguồn). Số điểm trên MN dao động cùng pha 2 nguồn là

   A. 10.                        B. 6.                          C. 13.                        D. 3.

12. Trên mặt chất lỏng có 2 nguồn sóng kết hợ A và B cách nhau 10 cm, cùng dao động vs tần số 80 Hz và pha ban đầu bằng 0. Vận tốc truyền sóng trên mặt chất lỏng là 40 cm/s. Điểm gần nhất nằm trên đường trung trực của AB dao động ngược pha với A và B cách trung điểm O của AB 1 đoạn là

   A. 1,6 cm.                 B. 2,29 cm.               C. 3,38 cm.               D. 4,58 cm.

13. Trên mặt chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 10 cm. Khi đó tại vùng giữa hai nguồn người ta quan sát thấy xuất hiện 10 dãy dao động cực đại và cắt đoạn AB thành 11 đoạn mà hai đoạn gần các nguồn chỉ dài bằng một nửa các đoạn còn lại. Biết tốc độ truyền sóng trên mặt chất lỏng đó là 50 cm/s. Tần số dao động củ a hai nguồn bằng

   A. 30 Hz.                   B. 25 Hz.                   C. 40 Hz.                   D. 15 Hz.

14. Trên mặt nước phẳng lặng có hai nguồn điểm dao động\[{{S}_{1}}v\grave{a}\text{ }{{S}_{2}}\] . Biết \[{{S}_{1}}{{S}_{2}}\] = 10 cm, tần số và biên độ dao động của \[{{S}_{1}},\text{ }{{S}_{2}}\] là ƒ = 120 Hz, a = 0,5 cm. Khi đó trên mặt nước, tại vùng giữa \[{{S}_{1}}v\grave{a}\text{ }{{S}_{2}}\]người ta quan sát thấy có 5 gợn lồi và những gợn này chia đoạn \[{{S}_{1}}{{S}_{2}}\] thành 6 đoạn mà hai đoạn ở hai đầu chỉ dài bằng một nữa các đoạn còn lại. Bước sóng \[\lambda \] có giá trị là:

A. \[\lambda \] = 4 cm. B. \[\lambda \] = 8 cm.  C. \[\lambda \] = 2 cm. D. \[\lambda \] = 6 cm.

15. Trên mặt chất lỏng có hai nguồn sóng kết hợp phát ra hai dao động\[{{u}_{1}}=\text{ }acos\omega t;\text{ }{{u}_{2}}=\text{ }asin\omega t\] . khoảng cách giữa hai nguồn là\[{{S}_{1}}{{S}_{2}}=\text{ }3,25\lambda \] . Hỏi trên đoạn \[{{S}_{1}}{{S}_{2}}\] có mấy điểm cực đại dao động cùng pha với \[{{u}_{2}}:\]              

A. 3 điểm.                     B. 4 điểm.                 C. 5 điểm.                 D. 6 điểm

16. Trên mặt chất lỏng có hai nguồn kết hợp \[{{S}_{1}},\text{ }{{S}_{2}}\] dao động với phương trình tượng ứng\[{{u}_{1}}=\text{ }acos\omega t\text{ }v\grave{a}\text{ }{{u}_{2}}=\text{ }asin\omega t\] . Khoảng cách giữa hai nguồn là\[{{S}_{1}}{{S}_{2}}=\text{ }2,75\lambda \] . Trên đoạn\[{{S}_{1}}{{S}_{2}}\] , số điểm dao động với biên độ cực đại và cùng pha với \[{{u}_{1}}\] là:

 A. 3 điểm                     B. 4 điểm.                 C. 5 điểm.                 D. 6 điểm.

17. Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn \[{{S}_{1}}{{S}_{2}}=\text{ }9\lambda \] phát ra dao động cùng pha nhau. Trên đoạn\[{{S}_{1}}{{S}_{2}}\] , số điểm có biên độ cực đại cùng pha với nhau và cùng pha với nguồn (không kể hai nguồn) là:

A. 12 B. 6                   C. 8                           D. 10

18. Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn \[{{S}_{1}}{{S}_{2}}=\text{ }9\lambda \]phát ra dao động\[u\text{ }=\text{ }cos\left( \omega t \right)\] . Trên đoạn\[{{S}_{1}}{{S}_{2}}\] , số điểm có biên độ cực đại cùng pha với nhau và ngược pha với nguồn (không kể hai nguồn) là:

 A. 8. B. 9                   C. 17.                        D. 16.

19. Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoản 8cm. Hỏi trên đoạn CO, số điểm dao động cùng pha với nguồn là:                           

A. 2 B. 3                     C. 4                           D. 5

20. Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6 cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoảng 8 cm. Hỏi trên đoạn CO, số điểm dao động ngược pha với nguồn là:                          

A. 2 B. 3                     C. 4                           D. 5

Bài viết gợi ý: