Bài tập lượng tử ánh sáng có lời giải chi tiết (Phần 2)

1. Tóm tắt lý thuyết và công thức:

   Tiên đề Bo : $\varepsilon =h{{f}_{nm}}=\frac{hc}{{{\lambda }_{nm}}}={{E}_{n}}-{{E}_{m}}$

+ Bán kính quỹ đạo dừng thứ n của electron trong nguyên tử hiđrô:

                           r_n = n²r₀   Với r₀ =5,3.10^-11m là bán kính Bo (ở quỹ đạo K)

+ Khi nguyên tử đang ở mức năng lượng cao chuyển xuống mức năng lượng thấp thì phát ra  photon, ngược lại chuyển từ mức năng lượng thấp chuyển lên mức năng lượng cao nguyên tử sẽ hấp thu photon

                                                                     

 

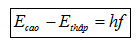
+Bước sóng phát ra khi nguyên tử chuyển mức năng lượng:$\varepsilon ={{E}_{n}}-{{E}_{m}}$

           

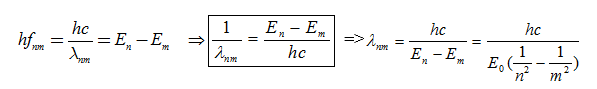
+Tần số của phôtôn bức xạ . 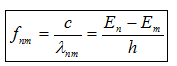             Với  E_n > E_m.

+Mối liên hệ giữa các bước sóng và tần số của các vạch quang phổ của nguyên từ hiđrô

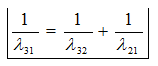                                                          và  ${{f}_{31}}={{f}_{32}}+{{f}_{21}}$ (như cộng véctơ)

+Công thức thực nghiệm: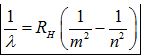            

+Hằng số Rydberg: ${{R}_{H}}=\frac{{{E}_{0}}}{h.c}=\frac{13,6.e}{h.c}=1,{{0969140.10}^{7}}m=1,{{097.10}^{7}}m$

Các dãy Quang phổ của nguyên tử hidrô

- Dãy Laiman: khi e ( n>1) về quĩ đạo K(m=1) thì phát ra các vạch thuộc dãy  Laiman: m = 1; n = 2,3,4…

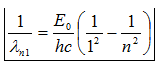                                                   với  $n\ge 2$   Các vạch thuộc vùng tử ngoại

- Dãy Banme: Khi e chuyển từ quĩ đạo ngoài (n>2) về quĩ đạo L(m=2) thì phát ra các vạch thuộc dãy Banme .   m = 2; n = 3,4,5…:    

         

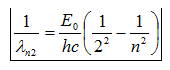
với $n\ge 3$  Gồm 4 vạch : đỏ ${{H}_{\alpha }}(0,656\mu m)$ , lam ${{H}_{\beta }}(0,486\mu m)$ ,

                                    chàm ${{H}_{\gamma }}(0,434\mu m)$,  tím ${{H}_{\delta }}(0,410\mu m)$và một phần ở vùng tử ngoại

Dãy Pasen : khi các e chuyển từ quĩ đạo bên ngoài (n>3) về quĩ đạo M(m=3) : m = 3; n  = 4,5,6…:     

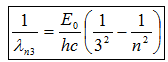                                                 với $n\ge 4$   Các vạch thuộc vùng hồng ngoại

Năng lượng của êlectron trong nguyên tử Hiđrô có biểu thức: 

+Năng lượng electron trong nguyên tử hiđrô: 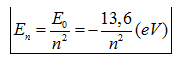   Với lượng tử số

             

E₀ = - 13,6eV: năng lượng ở trạng thái cơ bản ( Chú ý E₀ < 0 )

-n = 1 ứng với quỹ đạo K ( năng lượng thấp nhất )

-n = 2 ứng với quỹ đạo L...

    – $m=1;\quad n=2,\ 3,\ 4,\ ...$dãy Laiman (tử ngoại);

    – $m=2;\quad n=\ 3,\ 4,\ 5...$dãy Banme (một phần nhìn thấy)

    – $m=3;\quad n=\ 4,\ 5,6,...$dãy Pasen (hồng ngoại).

 Các bức xạ của dãy Banmer( nhìn thấy):

   + Vạch đỏ  ${{H}_{\alpha }}$: ${{\lambda }_{\alpha }}={{\lambda }_{ML}}={{\lambda }_{32}}$: $\frac{hc}{{{\lambda }_{32}}}={{E}_{3}}-{{E}_{2}}$

   + Vạch lam ${{H}_{\beta }}$:${{\lambda }_{\beta }}={{\lambda }_{NL}}={{\lambda }_{42}}$: $\frac{hc}{{{\lambda }_{42}}}={{E}_{4}}-{{E}_{2}}$

   + Vạch chàm${{H}_{\gamma }}$:${{\lambda }_{\gamma }}={{\lambda }_{OL}}={{\lambda }_{52}}$: $\frac{hc}{{{\lambda }_{52}}}={{E}_{5}}-{{E}_{2}}$

   + Vạch tím  ${{H}_{\theta }}$:${{\lambda }_{\theta }}={{\lambda }_{PL}}={{\lambda }_{62}}$: $\frac{hc}{{{\lambda }_{62}}}={{E}_{6}}-{{E}_{2}}$

                

                                       

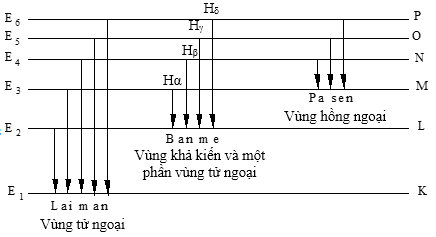
Các vạch có bước sóng dài nhất của các dãy:

   + Dãy Laiman: ${{\lambda }_{21}}$: $\frac{hc}{{{\lambda }_{21}}}={{E}_{2}}-{{E}_{1}}$;   + Dãy Banmer:${{\lambda }_{32}}$: $\frac{hc}{{{\lambda }_{32}}}={{E}_{3}}-{{E}_{2}}$;  + Dãy Paschen:${{\lambda }_{43}}$:$\frac{hc}{{{\lambda }_{43}}}={{E}_{4}}-{{E}_{3}}$

Chú ý: Khi nguyên tử ở trạng thái kích thích thứ n có thể (khả dĩ) phát ra số bức xạ điện từ cho bởi:

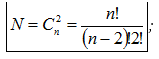trong đó $C_{n}^{2}$ là tổ hợp chập 2 của n.

 

2.Các dạng bài tập:   

DẠNG 1: Tìm năng lượng của một photon, tần số hay bước sóng:

Hướng dẫn: Áp dụng công thức $\varepsilon =hf=\frac{hc}{\lambda }$. Hay ${{E}_{cao}}-{{E}_{th\hat{a}p}}=hf$  để suy ra các đại lượng chưa biết.

Ví dụ 1: Chiếu một chùm sáng đơn sắc có bước sóng bằng 0,72 \[\mu m\]. Tìm tần số và năng lượng photon?

HD Giải :  Áp dụng công thức f=c/\[\lambda \] và $\varepsilon =hf=\frac{hc}{\lambda }$

Ví dụ 2:   Êlectron trong nguyên tử hiđrô chuyển từ mức năng lượng thứ 3 về mức năng lượng thứ nhất. Tính năng lượng phôtôn phát ra và tần số của phôtôn đó. Cho biết năng lượng của nguyên tử hiđro ở mức năng lượng thứ n là E_n = -$\frac{13,6}{{{n}^{2}}}(eV)$. Hằng số Plăng h = 6,625.10^-34 (J.s)

HD Giải : Tính $\Delta $E và f của phôtôn.

Năng lượng của phôtôn phát ra :    $\Delta E={{E}_{3}}-{{E}_{1}}=-13,6\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{1}^{2}}} \right)=12,088(eV)$.  

Tần số dao động của phôtôn :            f = $\frac{\Delta E}{h}\approx 2,{{92.10}^{15}}(Hz)$.

 

DẠNG 2:  Tìm động năng cực đại của electron khi xảy ra hiên tượng quang điện:

Hướng dẫn: Công thức: $\varepsilon =hf=\frac{hc}{\lambda }=A+\frac{mv_{0M\text{ax}}^{2}}{2}$ với \[{{E}_{}}=\frac{mv_{m\text{ax}}^{2}}{2}\] từ đó suy ra E_đ. Lưu ý: 1eV=1,6.10^-19J

Ví dụ 1:  Catốt của tế bào quang điện làm bằng vônfram, biết công thoát của electron với vônfram là 7,2.10^-19J. Chiếu vào catốt ánh sáng có bước sóng \[\lambda =0,18\mu m\]. Động năng cực đại của êlectrôn khi bức ra khỏi catôt là bao nhiêu?

HD Giải:  Công thức $\varepsilon =hf=\frac{hc}{\lambda }=A+\frac{mv_{0M\text{ax}}^{2}}{2}$. với \[{{E}_{}}=\frac{mv_{m\text{ax}}^{2}}{2}\]Từ đó ta suy ra E_đmax

Mở rộng: bài toán tương tự tìm Vmax ta cũng tìm E_đmax ...

 

DẠNG 3: Tìm vận tốc cực đại của electron khi đập vào catot.

Hướng dẫn: Vận dụng công thức: E_đ = A = |e|U_AK là năng lượng do điện trường cung cấp:       

                     \[/e/{{U}_{AK}}=Ed=\frac{mv_{{}}^{2}}{2}\]_. Từ đó suy ra được v

Ví dụ 1:  Hiệu điện thế giữa Anot và catot của ống Culitzơ là  20kV. Cho e=1,6.10^-19C, h=6,625.10^-34Js, c=3.10⁸m/s. Bỏ qua động năng ban đầu của electron. Tính vận tốc của electron khi đập vào catot?

HD Giải:  Vận dụng công thức  E_đ=A=|e| U_AK và |e|U_AK=E_đ=mv²/2 .  ta có v=8,4.10⁷m/s.

DẠNG 4: Tìm số electron bay ra khỏi anot, số photon đập vào anot trong một thời gian t bất kỳ. Tìm hiệu suất quang điện.

Hướng dẫn:

-Tìm số electron bay ra khỏi catot là số electron tạo ra dòng quang điện do vậy ta vận dụng công thức: I=q/t=n_e|e|/t  từ đó suy ra n_e

-Tìm số photon đập vào anot: Ta tìm năng lượng của chùm photon và lấy năng lượng của chùm photon chia cho năng lượng của một photon thì ta có số photon cần tìm. Với bài toán này đề thường cho công suất bức xạ P nên ta có: n_p=A_p/$\varepsilon $=P.t/hf.

- Muốn tìm hiện suất quang điện ta dùng công thức:  H=n_e/n_p

Ví dụ 1: : Chiếu một chùm bức xạ vào tế bào quang điện có catot làm bằng Na thì cường độ dòng quang điện bão hòa là 3\[\mu A\]. Số electron bị bứt ra ra khỏi catot trong hai phút là bao nhiêu?

HD Giải: Áp dụng công thức I=q/t=n_e|e|/t   ta suy ra được n_e=I.t/|e|. Lưu ý đổi đơn vị của I ra ampe

 

Ví dụ 2:  Chiếu vào catốt một ánh sáng có bước sóng 0,546μm, thì dòng quang điện bảo hoà có giá trị là 2mA. Công suất bức xạ là 1,515W . Hiệu suất lượng tử là bao nhiêu ?.

HD Giải :  Áp dụng công thức : I=q/t=n_e|e|/t  ta tìm được n_e; công thức n_p=A_p/$\varepsilon $=P.t/hf.  

                   ta tìm được n_p và công thức H=n_e/n_p  để tìm H. Lưu ý:H tính ra %

 

DẠNG 5: Tìm hiệu điện thế hãm để không một electron bay về anot (hay dòng quang điện triệt tiêu)

Hướng dẫn: - Hiện tượng các electron không về được anot do điện trường sinh công cản cản trở chúng.

-Muốn vậy thì: Công cản điện trường có giá trị bé nhất bằng động năng ban đầu cực đại của các electron quang điện. Ta có: \[\left| e{{U}_{h}} \right|=\frac{mv_{0M\text{ax}}^{2}}{2}\]suy ra: U_h=$\frac{mv_{0}^{2}}{2|e|}$

-Lưu ý: Khi chọn kết quả thì U_h<0. Trong bài toán trắc nghiệm nếu không có giá trị âm thì chọn giá trị độ lớn.

Ví dụ 1:  Chiếu một ánh sáng có bước sóng 0,45$\mu m$ vào catot của một tế bào quang điện. Công thoát kim loại làm catot là 2eV. Tìm hiệu điện thế giữa anot và catot để dòng quang điện triệt tiêu?

HD Giải:  Vận dụng U_h=$\frac{mv_{0}^{2}}{2|e|}$   nhưng ta phải tìm E_đ=$\varepsilon $-A. Với E_đ=$\frac{1}{2}mv_{0}^{2}$ Từ đó ta tìm được U_h=-0,76V

 

DẠNG 6: Xác định bước sóng ánh sáng (hay tần số) mà photon phát ra trong quá trình nguyên tử chuyển từ quỹ đạo có năng lượng cao về quỹ đạo có mức năng lượng thấp hơn.

Hướng dẫn: - Khi chuyển từ mức năng lượng cao về mức thấp thì nguyên tử phát ra photon có năng lượng:

                        $\varepsilon =h{{f}_{nm}}=\frac{hc}{{{\lambda }_{nm}}}={{E}_{n}}-{{E}_{m}}$(E_n>E­_m) (10)    từ đó suy ra được: Bước sóng hay tần số.

                      - Lưu ý: thường ta lên vẽ biểu đồ mức lượng để giải.

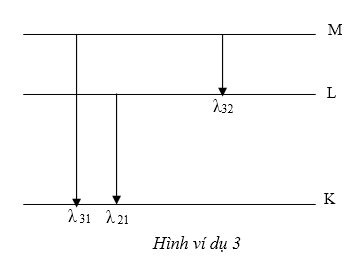
Ví dụ 1:  Nguyên tử Hydro bị kích thích chuyển lên quỹ đạo có năng lượng cao. Sau đó chuyển từ quỹ đạo có lượng E₃ về E₁ thì phát ra ánh sáng đơn sắc có tần số f₃₁=4200Hz. Khi chuyển từ E₃ về E₂ thì phát ra ánh sáng đơn sắc có tần số f₃₂= 3200Hz. Tìm tần số ánh sáng khi nó chuyển từ mức năng lượng E₂ về E₁?

HD Giải :  Vận dụng công thức $\varepsilon =h{{f}_{nm}}=\frac{hc}{{{\lambda }_{nm}}}={{E}_{n}}-{{E}_{m}}$(E_m>E­_n) (10)  ta có:

                   E₃-E₁=(E₃-E₂)+(E₂-E₁) $\Leftrightarrow $hf₃₁=hf₃₂+hf₂₁ $\Leftrightarrow $f₃₁=f₃₂+f₂₁ Suy ra:f₂₁=f₃₁-f₃₂

                   Mở rộng: Nếu tìm bước sóng ta cũng có: $\frac{1}{{{\lambda }_{31}}}=\frac{1}{{{\lambda }_{32}}}+\frac{1}{{{\lambda }_{21}}}$ từ đây suy ra các bước sóng cần tìm.

Ví dụ 2:  Trong quang phổ hiđrô, bước sóng λ (μm) của các vạch quang phổ như sau: Vạch thứ nhất của dãy Lai-man λ₂₁ =0,1216 μm; Vạch H_α của dãy Ban-me λ_­Hα = 0,6563μm.Vạch đầu của dãy Pa-sen λ₄₃ =1,8751μm

 Tính bước sóng của hai vạch quang phổ thứ hai, thứ ba của dãy Lai-man và của vạch H_β .

                                             

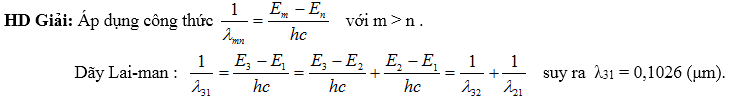
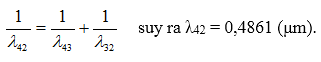
Ví dụ 3: Khi kích thích nguyên tử hiđro ở trạnh thái cơ bản, bán kính quỹ đạo dừng của êlectron tăng lên 9 lần. Tính các bước sóng của các bức xạ mà nguyên tử hiđro có thể phát ra, biết rằng năng lượng của các trạng thái dừng của nguyên tử hiđrô là E_n = $-\frac{13,6}{{{n}^{2}}}(eV)$ với n = 1;2;… Cho : h = 6,625.10^-34 (J.s) ; c = 3.10⁸ (m/s).

 

HD Giải: Nguyên tử hiđro ở trạng thái kích thích, êlectron ở trạng thái dừng ứng với n² = 9 => n =3

 

Sau đó electron trở về lớp trong có thể phát ra các bức xạ có bước sóng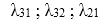

• Dãy Lai-man .                                                                                               

                                                                                                                                                            

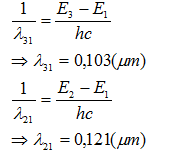
          Dãy Ban-me .

          $\frac{1}{{{\lambda }_{32}}}=\frac{{{E}_{3}}-{{E}_{2}}}{hc}\Rightarrow {{\lambda }_{32}}=0,657(\mu m)$      

                                                                 

       3.Bài tập có lời giải hoặc hướng dẫn:

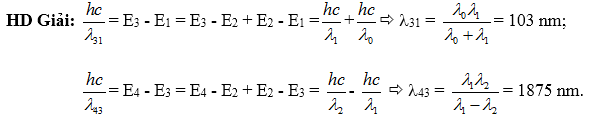
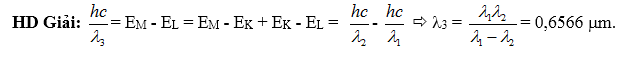
HD Giải:

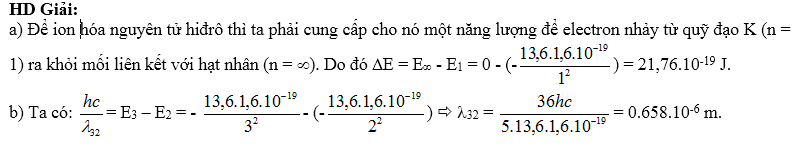
HD Giải:   E₃ = - $\frac{13,6}{{{3}^{2}}}$eV = - 1,511 eV; E₂ = - $\frac{13,6}{{{2}^{2}}}$eV = - 3,400 eV;

                   E₃ - E₂ = $\frac{hc}{{{\lambda }_{32}}}$ suy ra 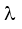₃₂ = $\frac{hc}{{{E}_{3}}-{{E}_{2}}}$ = 6,576.10^-7 m = 0,6576 mm.

 

HD Giải: 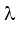  _LK = $\frac{hc}{{{E}_{L}}-{{E}_{K}}}$= 0,1218.10^-6m; 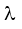_MK = $\frac{hc}{{{E}_{M}}-{{E}_{K}}}$= 0,1027.10^-6m;

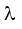                   _NK = $\frac{hc}{{{E}_{N}}-{{E}_{K}}}$= 0,0974.10^-6m; 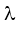_OK = $\frac{hc}{{{E}_{O}}-{{E}_{K}}}$= 0,0951.10^-6m.

HD Giải:  $\frac{hc}{{{\lambda }_{\alpha }}}$= E_M - E_L = E_M - E_K - (E_L - E_K) = $\frac{hc}{{{\lambda }_{L2}}}$- $\frac{hc}{{{\lambda }_{L1}}}$ suy ra 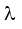_a =$\frac{{{\lambda }_{L1}}{{\lambda }_{L2}}}{{{\lambda }_{L1}}-{{\lambda }_{L2}}}$= 0,6739 mm.

                 $\frac{hc}{{{\lambda }_{L2}}}$= E_M – E_K suy ra E_K = - E_M - $\frac{hc}{{{\lambda }_{L2}}}$= - 13,54 eV; E_L = E_K + $\frac{hc}{{{\lambda }_{L1}}}$= - 3,36 eV.

HD Giải:  n = $\frac{W}{\varepsilon }=\frac{W}{\frac{hc}{\lambda }}=\frac{W\lambda }{hc}$; n’ = $\frac{W'}{\varepsilon '}=\frac{W'}{\frac{hc}{\lambda '}}=\frac{W'\lambda '}{hc}$; suy ra H = $\frac{n'}{n}=\frac{W'\lambda '}{W\lambda }=\frac{0,01W\lambda '}{W\lambda }$= 0,017 = 1,7 %.

ĐS: a. ${{f}_{21}}=2,{{469.10}^{15}}Hz$  

       b. ${{\lambda }_{31}}0,102523\mu m$.....

4. Luyện tập trắc nghiệm:

Câu 1: Trong nguyên tử hyđrô, xét các mức năng lượng từ K đến P có bao nhiêu khả năng kích thích để êlêctrôn tăng bán kính quỹ đạo lên 4 lần ?

A. 1                               B.  2                                C.  3 *                           D.  4

Câu 2 : Trong nguyên tử hiđrô, êlectrôn từ quỹ đạo L chuyển về quỹ đạo K có năng lượng E_K = –13,6eV. Bước sóng bức xạ phát ra bằng là l=0,1218mm. Mức năng lượng ứng với quỹ đạo L bằng :

A.  3,2eV                       B. –3,4eV *                     С. –4,1eV                      D. –5,6eV

Câu 3 : Chùm nguyên tử H đang ở trạng thái cơ bản, bị kích thích  phát sáng thì chúng có thể phát ra tối đa 3 vạch quang phổ. Khi bị kích thích electron trong nguyên tử H đã chuyển sang quỹ đạo :

      A.  M *                          B.  L                                C.  O                             D.  N 

Câu 4: Cho: 1eV = 1,6.10^-19J ; h = 6,625.10^-34Js ; c = 3.10⁸m/s . Khi êlectrôn (êlectron) trong nguyên tử hiđrô chuyển từ quĩ đạo dừng có năng lượng E_m = - 0,85eV sang quĩ đạo dừng có năng lượng E = - 13,60eV thì nguyên tử phát bức xạ điện từ có bước sóng

      A. 0,0974 μm.*             B. 0,4340 μm.                 C. 0,4860 μm.               D. 0,6563 μm.

Câu 5 : Trong nguyên tử hiđrô, bán kính Bo là r_o = 5,3.10^-11m. Bán kính quỹ đạo dừng N là

      A. 47,7.10^-11m.             B. 84,8.10^-11m.*              C. 21,2.10^-11m.             D. 132,5.10^-11m.

HD:  Quỹ đạo dừng N ứng với n = 4  => r = n²r₀ = 16.5,3.10^-11 = 8,48.10^-10m.= 84,8.10^-11m.*

Câu 6: Cho bán kính quỹ đạo Bo thứ nhất 0,53.10^-10 m. Bán kính quỹ đạo Bo thứ năm là:

     A. 2,65. 10^-10 m            B. 0,106. 10^-10 m               C. 10,25. 10^-10 m           D. 13,25. 10^-10 m

Câu 7 : Biết hằng số Plăng h = 6,625.10^-34J.s và độ lớn của điện tích nguyên tố là 1,6.10^-19C. Khi nguyên tử hiđrô chuyển từ trạng thái dừng có năng lượng -1,514 eV sang trang thái dừng có năng lượng -3,407 eV thì nguyên tử phát ra bức xạ có tần số

      A. 2,571.10¹³ Hz.          B. 4,572.10¹⁴Hz.*           C. 3,879.10¹⁴Hz.          D. 6,542.10¹²Hz.

Câu 8: Cho: 1eV = 1,6.10^-19 J; h = 6,625.10^-34 J.s; c = 3.10⁸ m/s. Khi êlectrôn (êlectron) trong nguyên tử hiđrô chuyển từ quĩ đạo dừng có năng lượng -0,85 eV sang quĩ đạo dừng có năng lượng -13,60 eV thì nguyên tử phát bức xạ điện từ có bước sóng

      A. 0,4340 mm                B. 0,4860 mm                  C. 0,0974 mm *             D. 0,6563 mm

Câu 9.,Một nguyên tử hiđrô chuyển từ trạng thái dừng có năng lượng  E_M = -1,5eV sang trạng thái năng lượng E_L = -3,4ev Bước sóng của bức xạ phát ra là:

      A. 0,434mm                 B. 0,486mm                       C. 0,564                      D. 0,654mm*

Câu 10. Bước sóng dài nhất trong dãy Banme là 0,6560 μm. Bước sóng dài nhất trong dãy Laiman là 0,1220 μm. Bước sóng dài thứ hai của dãy Laiman là

      A. 0,0528 μm                  B. 0,1029 μm*                       C. 0,1112 μm                  D. 0,1211 μm

 

  Câu 11: Trong quang phổ vạch của hiđrô bước sóng dài nhất trong dãy Laiman bằng 1215A⁰ , bước sóng ngắn nhất trongdãy Ban-me bằng 3650A⁰ .Tìm năng lượng ion hoá nguyên tử hiđro khi electron ở trên quỹ đạo có năng lương thấp nhất là : ( cho h= 6,625.10^-34Js ; c= 3.10⁸m/s    ;  1A⁰=10^-10 m)

 A. 13,6(ev)                        B. -13,6(ev)                         C. 13,1(ev)                            D. -13,1(ev)

    Câu 12. Mức năng lượng của các quỹ đạo dừng của nguyên tử hiđrô lần lượt từ trong ra ngoài là E₁ = - 13,6 eV; E₂ = - 3,4 eV; E₃ = - 1,5 eV; E₄ = - 0,85 eV. Nguyên tử ở trạng thái cơ bản có khả năng hấp thụ các phôtôn có năng lượng nào dưới đây để nhảy lên một trong các mức trên:

   A. 12,2 eV                   B. 3,4 eV                            C. 10,2 eV                       D. 1,9 eV

Câu 13. Cho h = 6,625.10^-34J.s ; c = 3.10⁸ m/s. Mức năng lượng của các quỹ đạo dừng của nguyên tử hiđrô lần lượt từ  trong ra ngoài là – 13,6 eV; - 3,4 eV; - 1,5 eV … với: E_n = $-\frac{13,6}{{{n}^{2}}}\text{ eV}$; n = 1, 2, 3 …

Khi electron chuyển từ mức năng lượng ứng với n = 3 về n = 1 thì sẽ phát ra bức xạ có tần số:

   A. 2,9.10¹⁴ Hz               B. 2,9.10¹⁵ Hz                   C. 2,9.10¹⁶ Hz                                   D. 2,9.10¹⁷ Hz

Câu 14. Một electron có động năng 12,4 eV đến va chạm với nguyên tử hiđrô đứng yên, ở trạng thái cơ bản. Sau va chạm nguyên tử hiđrô vẫn đứng yên nhưng chuyển lên mức kích thích đầu tiên. Động năng của electron còn lại là:     

A. 10,2 eV                     B. 2,2 eV                     C. 1,2 eV                              D. Một giá trị khác.

Câu 15: Khi electron ở quĩ đạo dừng thứ n thì năng lượng của nguyên tử Hydro được tính theo công thức ${{E}_{n}}=-\frac{13,6}{{{n}^{2}}}$eV (n = 1, 2, 3, ...). Khi electron trong nguyên tử Hydro chuyển từ quĩ đạo dừng thứ n = 3 sang quĩ đạo dừng n = 2 thì nguyên tử Hydro phát ra photon ứng với bức xạ có bước sóng bằng:

   

Câu 16: Bước sóng ứng với bốn vạch quang phổ Hyđro là vạch tím: $0,4102\mu m$; vạch chàm: $0,4340\mu m$; vạch lam: $0,4861\mu m$; vạch đỏ: $0,6563\mu m$. Bốn vạch này ứng với sự chuyển của êlectron trong nguyên tử Hyđro từ các quỹ đạo M, N, O và P về quỹ đạo L. Hỏi vạch lam ứng với sự chuyển nào ?

    A. Sự chuyển $M\to L$  B. Sự chuyển \[N\to L\]     C. Sự chuyển $O\to L$      D. Sự chuyển $P\to L$

 

Bài viết gợi ý: