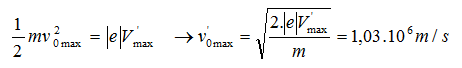1. Các công thức
+Năng lượng của phôtôn ánh sáng
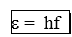
Trong chân không: e = $\frac{hc}{\lambda }$.
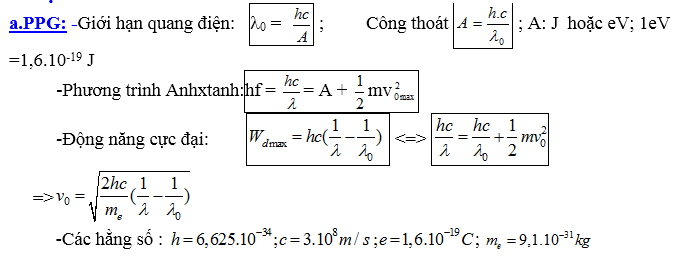
+Công thức Anhxtanh:
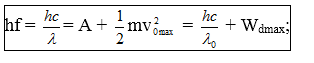
+Giới hạn quang điện :
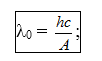
+ Công thoát của e ra khỏi kim loại 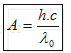
v0Max là vận tốc ban đầu của electron quang điện khi thoát khỏi catốt
f, l là tần số, bước sóng của ánh sáng kích thích
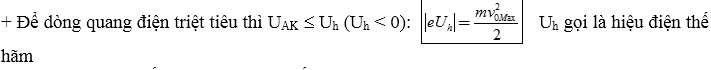
Lưu ý: Trong một số bài toán người ta lấy Uh > 0 thì đó là độ lớn.
+ Xét vật cô lập về điện, có điện thế cực đại VMax và khoảng cách cực đại dMax mà electron chuyển động trong điện trường cản có cường độ E được tính theo công thức: $\left| e \right|{{V}_{M\text{ax}}}=\frac{1}{2}mv_{0M\text{ax}}^{2}=\left| e \right|E{{d}_{M\text{ax}}}$
+ Với U là hiệu điện thế giữa anot và catot, vA là vận tốc cực đại của electron khi đập vào anốt, vK = v0Max là vận tốc ban đầu cực đại của electron khi rời catốt thì:
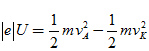
+Số hạt photôn đập vào: 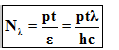
+Công suất của nguồn sáng: 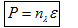
${{n}_{\lambda }}$ là số photon phát ra trong mỗi giây.$\varepsilon $ là lượng tử ánh sáng.
+Cường độ dòng quang điện bão hòa: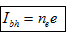 (Giả sử n= ne , với n là số electron đến được Anốt)
(Giả sử n= ne , với n là số electron đến được Anốt)
${{n}_{e}}$ là số quang electron bức ra khỏi catot mỗi giây = n số electron tới anot mỗi giây
$e$ là điện tích nguyên tố.
+Hiệu điện thế hãm: 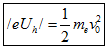
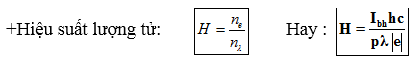
${{n}_{e}}$ là số electron bức ra khỏi catot kim loại mỗi giây. ${{n}_{\lambda }}$ là số photon đập vào catot trong mỗi giây.
2. Các hằng số Vật Lý và đổi đơn vị Vật Lý :
+Hằng số Plank: h = 6,625.10-34 J.s
+Vận tốc ánh sáng trong chân không: c = 3.108 m/s
+Điện tích nguyên tố : |e| = 1,6.10-19 C; hay e = 1,6.10-19 C
+Khối lượng của e : m (hay me ) = 9,1.10-31 kg
+Đổi đơn vị: 1eV=1,6.10-19J. 1MeV=1,6.10-13J.
3. Các dạng bài tập: Cho 1 eV = 1,6.10-19 J ; h = 6,625.10-34 Js ; c = 3.108 m/s; me = 9,1.10-31 kg.
b.Các Ví dụ :
Ví dụ 1: Giới hạn quang điện của kẽm là lo = 0,35mm. Tính công thoát của êlectron khỏi kẽm?
HD giải: Từ công thức: \[{{\lambda }_{0}}=\frac{hc}{A}=>A=\frac{hc}{{{\lambda }_{0}}}\] \[=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{35.10}^{-6}}}\]=5,67857.10-19 J =3,549eV
Ví dụ 2: (TN-2008): Giới hạn quang điện của đồng (Cu) là λ0 = 0,30 μm. Biết hằng số h = 6,625.10-34 J.s và vận tốc truyền ánh sáng trong chân không c = 3.108 m/s. Công thoát của êlectrôn khỏi bề mặt của đồng là
A.6,625.10-19 J. B. 6,265.10-19 J. C. 8,526.10-19 J. D. 8,625.10-19 J.
HD Giải: Công thoát: $A=\frac{hc}{{{\lambda }_{0}}}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{3.10}^{-6}}}=\text{6,625}\text{.1}{{\text{0}}^{\text{-19}}}\text{ J}.$Đáp án A
Ví dụ 3: Gới hạn quang điện của Ge là 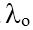 = 1,88mm. Tính năng lượng kích họat (năng lượng cần thiết để giải phóng một êlectron liên kết thành êlectron dẫn) của Ge?
= 1,88mm. Tính năng lượng kích họat (năng lượng cần thiết để giải phóng một êlectron liên kết thành êlectron dẫn) của Ge?
HD giải: Từ công thức: \[{{\lambda }_{0}}=\frac{hc}{A}=>A=\frac{hc}{{{\lambda }_{0}}}\] \[=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{1,{{88.10}^{-6}}}\]=1,057.10-19 J = 0,66eV
Ví dụ 4: Một kim loại có công thoát là 2,5eV. Tính giới hạn quang điện của kim loại đó :
A. 0,4969$\mu $m B. 0,649$\mu $m C. 0,325$\mu $m D. 0,229$\mu $m
HD Giải: Giới hạn quang điện \[{{\lambda }_{0}}=\frac{hc}{A}=\frac{{{6.625.10}^{-34}}{{.3.10}^{8}}}{2.5.1,{{6.10}^{-19}}}\] =4,96875.10-7 m = 0,4969mm .Đáp án A
Ví dụ 5: Giới hạn quang điện của KL dùng làm Kotot là 0,66mm. Tính:
1. Công thoát của KL dùng làm K theo đơn vị J và eV.
2. Tính động năng cực đại ban đầu và vận tốc cực đại của e quang điện khi bứt ra khỏi K, biết ánh sáng chiếu vào có bước sóng là 0,5mm .
HD giải: 1.\[{{\lambda }_{0}}=\frac{hc}{A}=>A=\frac{hc}{{{\lambda }_{0}}}\]=1,875eV=3.10-19 J .
2. \[{{W}_{d\max }}=hc(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}}\] ) = 9,63.10-20 J =>\[{{v}_{0}}=\sqrt{\frac{2hc}{{{m}_{e}}}(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}})}\]
Thế số:\[{{v}_{0}}=\sqrt{\frac{2.6,{{625.10}^{-34}}{{.3.10}^{8}}}{9,{{1.10}^{-31}}{{.10}^{-6}}}(\frac{1}{0,5}-\frac{1}{0,66})}\]= 460204,5326 = 4,6.105 m/s
Ví dụ 6: Catốt của một tế bào quang điện có công thoát bằng 3,5eV.
a. Tìm tần số giới hạn và giới hạn quang điện của kim loại ấy.
b. Khi chiếu vào catốt một bức xạ có bước sóng 250 nm có xảy ra hiện tượng quang điện không?
-Tìm hiệu điện thế giữa A và K để dòng quang điện bằng 0.
-Tìm động năng ban đầu cực đại của các êlectron quang điện.
-Tìm vận tốc của các êlectron quang điện khi bật ra khỏi K.
HD giải:
a.Tần số giới hạn quang điện: f = c/ 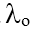 = A/h = 3,5.1,6.10-19/6,625.10-34 = 0,845.1015 Hz.
= A/h = 3,5.1,6.10-19/6,625.10-34 = 0,845.1015 Hz.
Giới hạn quang điện 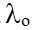 = hc/A = 6,625.10-34.3.108/3,5.1,6.10-19= 3,55.10-7m. =0,355 mm
= hc/A = 6,625.10-34.3.108/3,5.1,6.10-19= 3,55.10-7m. =0,355 mm
b. Vì 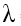 = 250 nm =0,250mm <
= 250 nm =0,250mm < 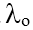 = 0,355 mm nên xảy ra hiện tượng quang điện
= 0,355 mm nên xảy ra hiện tượng quang điện
-Để dòng quang điện triệt tiêu thì công của điện trường phải triệt tiêu động năng ban đầu cực đại của êlectron quang.
\[e{{U}_{h}}=\frac{mv_{0}^{2}}{2}\Rightarrow {{U}_{h}}=\frac{mv_{0}^{2}}{2.e}=\frac{1}{e}(\frac{hc}{\lambda }-A)=\frac{1}{-1,{{6.10}^{-19}}}(\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{{{25.10}^{-8}}}-3,5.1,{{6.10}^{-19}})\] => Uh = - 1,47 V
-Động năng ban đầu cực đại \[\frac{mv_{0}^{2}}{2}=/e{{U}_{h}}/=1,47eV\]= 1,47.1,6.10-19 = 2,35.10-19J = 0,235.10-18J
Hay : Wđ =$\frac{mv_{0}^{2}}{2}=hc\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)=6,{{625.10}^{-34}}{{.3.10}^{8}}\left( \frac{1}{{{25.10}^{-8}}}-\frac{1}{35,{{5.10}^{-8}}} \right)$= 0,235.10-18J
-Vận tốc của êlectron ${{v}_{0}}=\sqrt{\frac{2{{W}_{}}}{m}}=\sqrt{\frac{2.0,{{235.10}^{-18}}}{9,{{1.10}^{-31}}}}=7,{{19.10}^{5}}$m/s.
Dạng 2: Liên hệ giữa động năng ban đầu( vận tốc ban đầu)và hiệu điện thế hãm giữa 2 cực của A và K để triệt tiêu dòng quang điện.
PPG. -PT Anhxtanh:
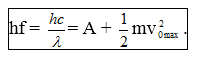
- Định lý động năng: \[\left| e.Uh \right|={{W}_{d\max }}\] => 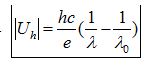
Ví dụ 1: Ta chiếu ánh sáng có bước sóng0,42 mm vào K của một tbqđ. Công thoát của KL làm K là 2eV. Để triệt tiêu dòng quang điện thì phải duy trì một hiệu điện thế hãmUAK bằng bao nhiêu?
HD Giải: \[\left| {{U}_{h}} \right|=\frac{hc}{e}(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}})\] Tính được Uh= - 0,95V
Ví dụ 2: Chiếu chùm bức xạ điện từ có tần số f = 5,76.1014 Hz vào một miếng kim loại thì các quang electron có vận tốc ban đầu cực đại là v = 0,4.106 m/s. Tính công thoát electron và bước sóng giới hạn quang điện của kim loại đó.
HD Giải : A = hf - $\frac{1}{2}mv_{0}^{2}$= 3,088.10-19 J; l0 = $\frac{hc}{A}$= 0,64.10-6 m.
Ví dụ 3: Công thoát electron khỏi kim loại natri là 2,48 eV. Một tế bào quang điện có catôt làm bằng natri, khi được chiếu sáng bằng chùm bức xạ có 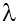 = 0,36 mm thì cho một dòng quang điện có cường độ bảo hòa là 3mA. Tính vận tốc ban đầu cực đại của electron quang điện và số electron bứt ra khỏi catôt trong 1 giây.
= 0,36 mm thì cho một dòng quang điện có cường độ bảo hòa là 3mA. Tính vận tốc ban đầu cực đại của electron quang điện và số electron bứt ra khỏi catôt trong 1 giây.
HD Giải: Wd0 = $\frac{hc}{\lambda }$- A = 1,55.10-19 J; v0 = $\sqrt{\frac{2{{W}_{d0}}}{m}}$= 0,58.106 m/s; ne = $\frac{{{I}_{bh}}}{e}$= 1,875.1013.
Ví dụ 4: Chiếu bức xạ có bước sóng 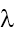 = 0,438 mm vào catôt của một tế bào quang điện. Biết kim loại làm catôt của tế bào quang điện có giới hạn quang điện là
= 0,438 mm vào catôt của một tế bào quang điện. Biết kim loại làm catôt của tế bào quang điện có giới hạn quang điện là 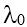 = 0,62 mm. Tìm điện áp hãm làm triệt tiêu dòng quang điện.
= 0,62 mm. Tìm điện áp hãm làm triệt tiêu dòng quang điện.
HD Giải : Wd0 = $\frac{hc}{\lambda }$- $\frac{hc}{{{\lambda }_{0}}}$= 1,33.10-19 J; Uh = - $\frac{{{W}_{d0}}}{e}$= - 0,83 V.
Ví dụ 5: Chiếu một bức xạ điện từ có bước sóng 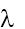 vào catôt của một tế bào quang điện. Biết công thoát electron của kim loại làm catôt là 3eV và các electron bắn ra với vận tốc ban đầu cực đại là 7.105 m/s. Xác định bước sóng của bức xạ điện từ đó và cho biết bức xạ điện từ đó thuộc vùng nào trong thang sóng điện từ.
vào catôt của một tế bào quang điện. Biết công thoát electron của kim loại làm catôt là 3eV và các electron bắn ra với vận tốc ban đầu cực đại là 7.105 m/s. Xác định bước sóng của bức xạ điện từ đó và cho biết bức xạ điện từ đó thuộc vùng nào trong thang sóng điện từ.
HD Giải : 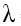 = $\frac{hc}{A+\frac{1}{2}mv_{0}^{2}}$= 0,215.10-6 m; bức xạ đó thuộc vùng tử ngoại.
= $\frac{hc}{A+\frac{1}{2}mv_{0}^{2}}$= 0,215.10-6 m; bức xạ đó thuộc vùng tử ngoại.
Ví dụ 6: Chiếu bức xạ có bước sóng 0,405mm vào một tấm kim loại thì các quang electron có vận tốc ban đầu cực đại là v1. Thay bức xạ khác có tần số 16.1014 Hz thì vận tốc ban đầu cực đại của các quang electron là v2 = 2v1. Tìm công thoát electron của kim loại.
HD Giải: f1 = $\frac{c}{\lambda _{1}^{{}}}$= 7,4.1014 Hz; $\frac{1}{2}mv_{1}^{2}$= hf1 – A; $\frac{1}{2}mv_{2}^{2}$= 4$\frac{1}{2}mv_{1}^{2}$= hf2 – A
ð 4 = $\frac{h{{f}_{2}}-A}{h{{f}_{1}}-A}$ð A = $\frac{4h{{f}_{1}}-h{{f}_{2}}}{3}$= 3.10-19 J.
Ví dụ 7: Chiếu bức xạ có bước sóng 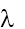 = 0,4 mm vào catôt của một tế bào quang điện. Biết công thoát electron của kim loại làm catôt là A = 2 eV, điện áp giữa anôt và catôt là UAK = 5 V. Tính động năng cực đại của các quang electron khi tới anôt.
= 0,4 mm vào catôt của một tế bào quang điện. Biết công thoát electron của kim loại làm catôt là A = 2 eV, điện áp giữa anôt và catôt là UAK = 5 V. Tính động năng cực đại của các quang electron khi tới anôt.
HD Giải : Wđ0 = $\frac{hc}{\lambda }$- A = 8,17.10-19 J; Wđmax = Wđ0 + |e|UAK = 16,17.10-19 J = 10,1 eV.
Ví dụ 8: Catot của tế bào quang điện làm bằng đồng, công thoát khỏi đồng là 4,47eV.
Cho biết: h = 6,625.10-34 (J.s) ; c = 3.108 (m/s) ; e = 1,6.10-19 (C).
a. Tính giới hạn quang điện của đồng.
b. Chiếu đồng thời 2 bức xạ điện từ có bước sóng λ1 = 0,210 (μm) và λ2 = 0,320 (μm) vào catot của tế bào quang điện trên, phải đặt hiệu thế hãm bằng bao nhiêu để triệt tiêu hoàn toàn dòng quang điện.
HD Giải :
a. Tính λ0 .Giới hạn quang điện của đồng: λ0 = $\frac{hc}{A}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{4,47.1,{{6.10}^{-19}}}=0,278($μm).
b. Tính Uh: λ1 < λ0 < λ2 do đó chỉ có λ1 gây ra hiện tượng quang điện.
Điều kiện để dòng quang điện triệt tiêu:$e\left| {{U}_{AK}} \right|=e{{U}_{h}}>{{W}_{\max }}$. ${{U}_{h}}>\frac{{{W}_{\max }}}{e}=\frac{1}{e}\left( \frac{hc}{\lambda }-A \right)=1,446(V)$
Ví dụ 9: Tính năng lượng, động lượng và khối lượng của photôn ứng với các bức xạ điện từ sau đây:
a. Bức xạ đỏ có λ = 0,76 μm.
b. Sóng vô tuyến có λ = 500 m.
c. Tia phóng xạ γ có f = 4.1017 KHz. Cho biết c = 3.108 m/s ; h = 6,625.10-34 J.s
HD Giải :
a. Bức xạ đỏ có λ = 0,76 μm.
- Năng lượng: ε = hf = $\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{76.10}^{-6}}}=26,{{15.10}^{-20}}(J)$
- Động lượng: ρ = $\frac{\varepsilon }{{{c}^{{}}}}=8,{{72.10}^{-28}}(kg.m/s)$. - Khối lượng: m = $\frac{\varepsilon }{{{c}^{2}}}$ = 2,9.10-36 (kg).
b. Sóng vô tuyến có λ = 500 m. Tương tự, ta có: - Năng lượng: ε = hf = $3,{{975.10}^{-28}}(J)$
- Động lượng: ρ = $\frac{\varepsilon }{{{c}^{{}}}}=1,{{325.10}^{-36}}(kg.m/s)$. - Khối lượng: m = $\frac{\varepsilon }{{{c}^{2}}}$ = 4,42.10-45 (kg).
c. Tương tự:- Năng lượng: ε = hf = 26,5.10-14 (J).
- Động lượng: ρ = $\frac{\varepsilon }{{{c}^{{}}}}=8,{{8.10}^{-22}}(kg.m/s)$. - Khối lượng: m = $\frac{\varepsilon }{{{c}^{2}}}$ = 0,94.10-31 (kg).
Dạng 3: Cho UAK> 0 hãy tính vận tốc của e khi đập vào Anot.
PPG: Gọi v là vận tốc của e khi đập vào Anot. Áp dụng định lí động năng:
\[\frac{1}{2}m{{v}^{2}}-\frac{1}{2}mv_{0}^{2}=e{{U}_{AK}}\]=> \[\frac{1}{2}m{{v}^{2}}=\frac{1}{2}mv_{0}^{2}+e{{U}_{AK}}\] => \[\frac{1}{2}m{{v}^{2}}=+\varepsilon -A+e{{U}_{AK}}\]
\[\frac{1}{2}m{{v}^{2}}=hc(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}})+e{{U}_{AK}}\]=> v ....
Dạng 4: Cho công suất của nguồn bức xạ. Tính số Phôton đập vào Katot sau thời gian t
PPG: Năng lượng của chùm photon rọi vào Katot sau khoảng thời gian t: W = P.t
-Số photon đập vào Katot: \[{{n}_{\lambda }}=\frac{W}{\varepsilon }=\frac{P.\lambda .t}{h.c}\]
-Công suất của nguồn : P = nλ.ε. (nλ là số photon tương ứng với bức xạ λ phát ra trong 1 giây).
-Cường độ dòng điện bão hoà : Ibh = ne.e .(ne là số electron quang điện từ catot đến anot trong 1 giây).
-Hiệu suất quang điện : H = $\frac{{{n}_{e}}}{{{n}_{\lambda }}}$
Ví dụ 1: Một ngọn đèn phát ra ánh sáng đơn sắc có 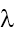 =0,6mm sẽ phát ra bao nhiêu photon trong 10s nếu công suất đèn là P = 10W.Giải: \[{{n}_{\lambda }}=\frac{W}{\varepsilon }=\frac{P.\lambda .t}{h.c}=\frac{10.0,{{6.10}^{-6}}.10}{{{6.625.10}^{-34}}{{.3.10}^{8}}}=3,{{0189.10}^{20}}\]= 3,02 .1020 photon
=0,6mm sẽ phát ra bao nhiêu photon trong 10s nếu công suất đèn là P = 10W.Giải: \[{{n}_{\lambda }}=\frac{W}{\varepsilon }=\frac{P.\lambda .t}{h.c}=\frac{10.0,{{6.10}^{-6}}.10}{{{6.625.10}^{-34}}{{.3.10}^{8}}}=3,{{0189.10}^{20}}\]= 3,02 .1020 photon
Ví dụ 2: Nguồn Laser mạnh phát ra những xung bức xạ có năng lượng \[W=3000J\]. Bức xạ phát ra có bước sóng $\lambda =480\ nm$. Tính số photon trong mỗi bức xạ đó?
HD Giải : Gọi số photon trong mỗi xung là $n$.($\varepsilon $ là năng lượng của một photon)
Năng lượng của mỗi xung Laser: \[W=n\varepsilon \] \[\Rightarrow n=\frac{W}{\varepsilon }=\frac{W.\lambda }{h.c}=\frac{{{3000.480.10}^{-9}}}{6,{{625.10}^{-34}}{{.3.10}^{8}}}=7,{{25.10}^{21}}\] photon
Dạng 5: Cho cường độ dòng quang điện bão hoà. Tính số e quang điện bật ra khỏi Katot sau khoảng thời gian t.
PPG: Điện lượng chuyển từ K đến A : q= Ibh.t = ne.e => \[{{n}_{e}}=\frac{q}{e}=\frac{{{I}_{bh.}}t}{e}\]
Gọi ne là số e quang điện bật ra ở Kaot ( 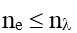 );
);
Gọi n là số e quang đến được Anốt ( 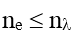 , Khi I = Ibh. Thì n = ne )
, Khi I = Ibh. Thì n = ne )
Lưu ý: Nếu đề không cho rõ % e quang điện bật ra về được Anot thì lúc đó ta có thể cho n= ne = nl
Ví dụ 1: Cho cường độ dòng quang điện bão bào là 0,32mA. Tính số e tách ra khỏi Katot của tế bào quang điện trong thời gian 20s biết chỉ 80% số e tách ra về được Anot.
HD Giải: H =$\frac{{{n}_{e}}}{{{n}_{\lambda }}}$= 0,8 => nl =\[\frac{{{n}_{e}}}{H}\] Hay: \[{{n}_{\lambda }}=\frac{{{I}_{bh.}}t}{e.H}\].Thế số: \[{{n}_{\lambda }}=\frac{0,{{32.10}^{-3}}.20}{1,{{6.10}^{-19}}.0,8}={{5.10}^{16}}hat\]
Ví dụ 2: Một tế bào quang điện có catôt làm bằng Asen có công thoát electron bằng 5,15 eV. Chiếu chùm sáng đơn sắc có bước sóng 0,20 mm vào catôt của tế bào quang điện thì thấy cường độ dòng quang điện bảo hòa là 4,5 mA. Biết công suất chùm bức xạ là 3 mW . Xác định vận tốc cực đại của electron khi nó vừa bị bật ra khỏi catôt và hiệu suất lượng tử.
HD Giải . Ta có: Wd0 = $\frac{hc}{\lambda }$- A = 1,7.10-19 J; v0 = $\sqrt{\frac{2{{W}_{d0}}}{m}}$= 0,6.106 m/s.
ne = $\frac{{{I}_{bh}}}{e}$= 2,8.1013; nl = $\frac{P}{\frac{hc}{\lambda }}=\frac{P\lambda }{hc}$= 3.1015 ð H = $\frac{{{n}_{e}}}{{{n}_{\lambda }}}$= 9,3.10-3 = 0,93%.
Dạng 6: Tính hiệu suất lượng tử của tế bào quang điện.
PPG: Hiệu suất lượng tử của tế bào quang điện là đại lượng được tính bằng tỉ số giữa số e quang điện bật ra khỏi Katot với số photon đập vào Katot.
H = $\frac{{{n}_{e}}}{{{n}_{\lambda }}}$ => \[H=\frac{\frac{{{I}_{bh.}}t}{e}}{\frac{P\lambda t}{hc}}=\frac{{{I}_{bh}}.hc}{e.P.\lambda }\] .
Ví dụ 1: Khi chiếu 1 bức xạ điện từ có bước sóng 0,5 micromet vào bề mặt của tế bào quang điện tạo ra dòng điện bão hòa là 0,32A. Công suất bức xạ đập vào Katot là P=1,5W. tính hiệu suất của tế bào quang điện.
HD Giải: \[H=\frac{{{I}_{bh}}.h.c}{e.P.\lambda }=\frac{0,32.6,{{625.10}^{-34}}{{.3.10}^{8}}}{1,{{6.10}^{-19}}.1,5.0,{{5.10}^{-6}}}.100%=53%\]
Ví dụ 2: Kim loại làm catot của tế bào quang điện có giới hạn quang điện 0,32 (μm). Chiếu ánh sáng có bước sóng 0,25 (μm) vào catot của tế bào quang điện trên.
Cho biết : h = 6,625.10-34 (J.s) ; c = 3.108 (m/s) ; me = 9,1.10-31 (kg) ; -e = -1,6.10-19 (C).
a) Tính vận tốc ban đầu cực đại của electron quang điện.
b) Biết rằng các electron thoát ra đều bị hút về anot, cường độ dòng quang điện bão hoà bằng 0,7 mA. Tính số electron thoát ra khỏi catot trong mỗi giây.
HD Giải: Ta có: $e\left| {{U}_{AK}} \right|=\frac{1}{2}mv_{0\max }^{2}$.
Phương trình Anh-xtanh : $\frac{hc}{\lambda }$ = $A+\frac{mv_{0\max }^{2}}{2}$ = A + eUh .
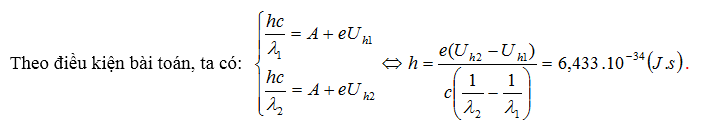
Ví dụ 3: Công thoát của êlectron đối với Natri là 2,48 (eV). Catot của tế bào quang điện làm bằng Natri được chiếu sáng bởi bức xạ có bước sóng λ = 0,36 (μm) thì có dòng quang điện bão hoà Ibh = 50 (mA).Cho biết:h = 6,625.10-34 (J.s); c = 3.10 (m/s) ; me = 9,1.10-31 (kg); - e = - 1,6.10-19 (C).
a) Tính giới hạn quang điện của Natri.
b) Tính vận tốc ban đầu cực đại của êlectron quang điện.
c) Hiệu suất quang điện bằng 60%, tính công suất của nguồn bức xạ chiếu vào catôt.
HD Giải:
a) Tính λ0. Giới hạn quang điện : λ0 = $\frac{hc}{A}=0,5($μm).
b) Tính v0. Phương trình Anh-xtanh:$\frac{hc}{\lambda }$ = $A+\frac{mv_{0\max }^{2}}{2}$.
Suy ra: ${{v}_{0\max }}=\sqrt{\frac{2}{{{m}_{e}}}\left( \frac{hc}{\lambda }-A \right)}=5,{{84.10}^{5}}\left( m/s \right)$
c) Tính P. Ta có Ibh = ne.e suy ra ne = $\frac{{{I}_{bh}}}{e}$. P = nλ.ε suy ra nλ = $\frac{P}{\varepsilon }$.
$H=\frac{{{n}_{e}}}{{{n}_{\lambda }}}$ do đó $P=\frac{{{I}_{bh}}.hc}{He\lambda }\approx 0,29$ (W).
Dạng 7: Ứng dụng của hiện tượng quang điện để tính các hằng số h, e, A.
Áp dụng các công thức:
- Năng lượng của phôtôn : ε = hf = h$\frac{c}{\lambda }$.
- Phương trình Anh-xtanh : ε = $A+\frac{mv_{0\max }^{2}}{2}$.
- Hiệu điện thế hãm : $e\left| {{U}_{AK}} \right|=e{{U}_{h}}=\frac{1}{2}mv_{0\max }^{2}$.
Ví dụ 1: Khi chiếu một chùm sáng vào một kim loại thì có hiện tượng quang điện xảy ra. Nếu dùng hiệu điện thế hãm bằng 3 (V) thì các êlectron quang điện bị giữ lại không bay sang anot
được. Cho biết giới hạn quang điện của kim loại đó là : λ0 = 0,5 (μm) ; h = 6,625.10-34 (J.s) ; c = 3.108 (m/s) ; -e = -1,6.10-19 (C). Tính tần số của chùm ánh sáng tới kim loại.
HD Giải :Các êlectron quang điện bị giữ lại hoàn toàn không qua được anot nên : $e\left| {{U}_{AK}} \right|=e{{U}_{h}}=\frac{1}{2}mv_{0\max }^{2}$
Phương trình Anh-xtanh : hf = A + $\frac{1}{2}mv_{0\max }^{2}$.
Hay hf = eUh + A = eUh + $\frac{hc}{{{\lambda }_{0}}}$ ; Suy ra: f = $\frac{e{{U}_{h}}}{h}+\frac{c}{{{\lambda }_{0}}}$.
Thay số, ta được : $f=\frac{1,{{6.10}^{-19}}.3}{6,{{625.10}^{-34}}}+\frac{{{3.10}^{8}}}{0,{{5.10}^{-6}}}=13,{{245.10}^{14}}(Hz)$.
Ví dụ 2: Chiếu bức xạ có bước sóng 0,35 (μm) vào một kim loại, các êlectron kim quang điện bắn ra đều bị giữ lại bởi một hiệu điện thế hãm. Khi thay chùm bức xạ có bước sóng giảm 0,05 (μm) thì hiệu điện thế hãm tăng 0,59 (V). Tính điện tích của êlectron quang điện. Cho biết : h = 6,625.10-34 (J.s) ; c = 3.108 (m/s).
HD Giải :Ta có $\frac{hc}{\lambda }$ = $A+\frac{mv_{0\max }^{2}}{2}$ = A + eUh ( Phương trình Anh-xtanh)
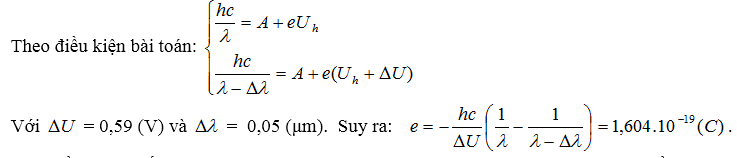
Ví dụ 3: Lần lượt chiếu hai bức xạ có bước sóng λ1 = 0,405 (μm), λ2 = 0,436 (μm) vào bề mặt của một kim loại và đo hiệu điện thế hãm tương ứng Uh1 = 1,15 (V); Uh2 = 0,93 (V). Cho biết: h = 6,625.10-34 (J.s) ; c = 3.108 (m/s) ; e = 1,6.10-19 (C). Tính công thoát của kim loại đó.
HD Giải :
Ta có: $\frac{hc}{\lambda }$ = $A+\frac{mv_{0\max }^{2}}{2}$ = A + eUh ( Phương trình Anh-xtanh)
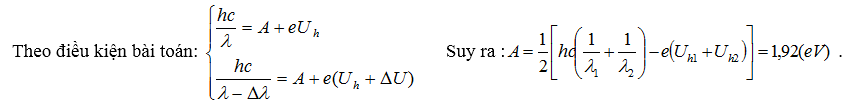
Dạng 8: Chiếu ánh sáng kích thích có bước sóng thích hợp vào bề mặt tấm KL (hay quả cầu) được cô lập về điện. Tính hiệu điện thế cực đại mà tấm KL đạt được.
PPG: Khi chiếu ánh sáng kích thích vào bề mặt KL thì e quang điện bị bật ra, tấm KL mất điện tử (-) nên tích điện (+) và có điện thế là V. Điện trường do điện thế V gây ra sinh ra 1 công cản AC = e.V ngăn cản sự bứt ra của các e tiếp theo. Nhưng ban đầu AC < Wdmax , nên e quang điện vẫn bị bứt ra. Điện tích (+) của tấm KL tăng dần, điện thế V tăng dần. Khi V =Vmax thì công lực cản có độ lớn đúng bằng Wdmax của e quang điện nên e không còn bật ra.
Ta có: \[e{{V}_{Max}}=\frac{1}{2}{{m}_{e}}v_{0\max }^{2}\] => \[e{{V}_{Max}}=\varepsilon -A=\frac{hc}{\lambda }-\frac{hc}{{{\lambda }_{0}}}\] Vậy \[{{V}_{Max}}=\frac{hc}{e}(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}})\]
Ví dụ 1: Một quả cầu bằng đồng (Cu) cô lập về điện được chiếu bởi 1 bức xạ điện từ có λ = 0,14 (μm), . Cho giới hạn quang điện của Cu là λ1 = 0,3 (μm). Tính điện thế cực đại của quả cầu.
HD Giải:\[{{V}_{Max}}=\frac{hc}{e}(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}})=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{1,{{6.10}^{-19}}}(\frac{1}{0,{{14.10}^{-6}}}-\frac{1}{0,{{3.10}^{-6}}})=4,73V\]
Ví dụ 2: Công thoát electron khỏi đồng là 4,57 eV. Chiếu bức xạ có bước sóng 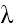 = 0,14 mm vào một quả cầu bằng đồng đặt xa các vật khác. Tính giới hạn quang điện của đồng và điện thế cực đại mà quả cầu đồng tích được.
= 0,14 mm vào một quả cầu bằng đồng đặt xa các vật khác. Tính giới hạn quang điện của đồng và điện thế cực đại mà quả cầu đồng tích được.
HD Giải: l0 = $\frac{hc}{A}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{4,57.1,{{6.10}^{-19}}}$= 0,27.10-6 m; Wd0 = $\frac{hc}{\lambda }$- A = 6,88.10-19 J; Vmax = $\frac{{{W}_{d0}}}{e}$= 4,3 V.
Ví dụ 3: Công thoát electron khỏi kẻm là 4,25 eV. Chiếu vào một tấm kẻm đặt cô lập về điện một chùm bức xạ điện từ đơn sắc thì thấy tấm kẻm tích được điện tích cực đại là 3 V. Tính bước sóng và tần số của chùm bức xạ.
HD Giải : Wd0max = eVmax = 3 eV; l = $\frac{hc}{A+{{\text{W}}_{\text{d0}m\text{ax}}}}$ = 0,274.10- 6 m; f = $\frac{c}{\lambda }$ = 1,1.1014 Hz.
4.Bài tập tổng hợp có hướng dẫn
Bài 1: Khi chiếu bức xạ có bước sóng 0,4 mm vào catốt của một tế bào quang điện, muốn triệt tiêu dòng quang điện thì hiệu điện thế giữa A và K bằng -1,25V.
a. Tìm vận tốc ban đầu cực đại của các e quang điện.
b. Tìm công thoát của các e của kim loại làm catốt đó (tính ra eV).
HD Giải :a. $\frac{mv_{0\max }^{2}}{2}=|e{{U}_{h}}|\Rightarrow {{v}_{0}}=\sqrt{\frac{2e{{U}_{h}}}{m}}=\sqrt{\frac{2.1,{{6.10}^{-19}}.1,25}{9,{{1.10}^{-31}}}}$= 0,663.106 m/s.
b. Công thoát: \[A=\frac{hc}{\lambda }-\frac{1}{2}mv_{0\max }^{2}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{4.10}^{-6}}}-\frac{1}{2}.9,{{1.10}^{-31}}.{{\left( 0,{{663.10}^{6}} \right)}^{2}}\]$=2,{{97.10}^{-19}}J=1,855eV$.

HD Giải :
a. ${{\lambda }_{0}}=\frac{hc}{A}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{4,5.1,{{6.10}^{-19}}}=0,276$ mm.
b. \[\frac{hc}{\lambda }=A+{{W}_{}}\Rightarrow \lambda =\frac{hc}{A+{{W}_{}}}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{4,5.1,{{6.10}^{-19}}+3,{{6.10}^{-19}}}=0,184\] mm.
c. \[\frac{hc}{\lambda '}=A+e{{U}_{h}}\Rightarrow \lambda '=\frac{hc}{A+e{{U}_{h}}}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{4,5.1,{{6.10}^{-19}}+\left( -1,5 \right).\left( -1,{{6.10}^{-19}} \right)}=0,207\] mm.
Bài 3: Công tối thiểu để bức một êlectron ra khỏi bề mặt một tấm kim loại của một tế bào quang điện là 1,88eV. Khi chiếu một bức xạ có bước sóng 0,489 mm thì dòng quang điện bão hòa đo được là 0,26mA.
a. Tính số êlectron tách ra khỏi catốt trong 1 phút.
b. Tính hiệu điện thế hãm để triệt tiêu hoàn toàn dòng quang điện.
HD Giải :
a. Ibh = n$\left| e \right|$ = 26.10-5A. (n là số êlectron tách ra khỏi catốt trong 1s). n = $\frac{{{26.10}^{-5}}}{1,{{6.10}^{-19}}}=16,{{25.10}^{14}}$;
Số êlectron tách ra khỏi K trong 1 phút: N=60n = 975.1014.
b. $e{{U}_{h}}=\frac{mv_{0}^{2}}{2}=\frac{hc}{\lambda }-A=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{489.10}^{-6}}.1,{{6.10}^{-19}}}-1,88eV=2,54-1,88=0,66eV$.Hiệu điện thế hãm Uh = – 0,66V.
Bài 4 : Catốt của một tế bào quang điện có công thoát là 2,26eV. Bề mặt catốt được chiếu bởi bức xạ có bước sóng 0,4mm.
a. Tính tần số của giới hạn quang điện.
b. Bề mặt catốt nhận được một công suất chiếu sáng là 3mW. Tính số phôtôn mà bề mặt catốt nhận được trong 30s.
c. Cho hiệu suất quang điện bằng 67%. Tính số êlectron quang điện bật ra trong mỗi giây và cường độ dòng quang điện bão hòa.
Hướng dẫn giải:
a. ${{f}_{0}}=\frac{c}{{{\lambda }_{0}}}=\frac{A}{h}=\frac{2,26.1,{{6.10}^{-19}}}{6,{{625.10}^{-34}}}=0,{{5458.10}^{15}}$Hz.
b. Gọi ${{n}_{\lambda }}$là số phôtôn chiếu đến tế bào quang điện trong 1s.
Công suất bức xạ: $P={{n}_{\lambda }}\varepsilon =\frac{{{n}_{\lambda }}hc}{\lambda }\Rightarrow {{n}_{\lambda }}=\frac{P\lambda }{hc}=\frac{{{3.10}^{-3}}.0,{{4.10}^{-6}}}{6,{{625.10}^{-34}}{{.3.10}^{8}}}=6,{{04.10}^{15}}$
Số phôtôn mà bề mặt catốt nhận được trong 30s: N=30${{n}_{\lambda }}$ =181,2.1015
c. Gọi $n'$ là số êlectron bị bật ra trong 1s: $n'=$67%${{n}_{\lambda }}$ = 4,0468.1015.
Cường độ dòng quang điện bão hòa: ${{I}_{bh}}=n'\left| e \right|={{n}_{e}}\left| e \right|=$4,0468.1015.1,6.10-19 =0,6475mA.
Bài 5 (*): Nguồn sáng có công suất $P=2\,\,W$, phát ra bức xạ có bước sóng $\lambda =0,597\mu m$ tỏa theo mọi hướng. Tính xem ở khoảng cách bao xa người ta còn có thể trông thấy được nguồn sáng này, biết rằng mắt còn thấy nguồn sáng khi có ít nhất $n=80$ photon lọt vào mắt trong 1 giây. Biết con ngươi có đường kính $d=4mm$. Bỏ qua sự hấp thụ photon của môi trường.
Hướng dẫn giải:
Số photon của nguồn sáng phát ra trong 1 giây: ${{n}_{\lambda }}=\frac{P}{\varepsilon }=\frac{P\lambda }{hc}$
Gọi D là khoảng cách từ mắt đến nguồn sáng, thì số photon trên được phân bố đều trên mặt hình cầu có bán kính là D.
Số photon qua 1 đơn vị diện tích của hình cầu trong 1 giây là: $k=\frac{{{n}_{\lambda }}}{4\pi {{D}^{2}}}=\frac{P\lambda }{hc.4\pi {{D}^{2}}}$
Số photon lọt vào con ngươi trong 1 giây là: $N=\pi {{\left( \frac{d}{2} \right)}^{2}}.k=\frac{\pi {{d}^{2}}}{4}.\frac{P\lambda }{hc.4\pi {{D}^{2}}}=\frac{P\lambda {{d}^{2}}}{16hc.{{D}^{2}}}$
Để mắt còn nhìn thấy được nguồn sáng thì $N\ge n=80$ ($n$ là độ nhạy của mắt – số photon ít nhất lọt vào măt mà mắt còn phát hiện ra).
Suy ra:
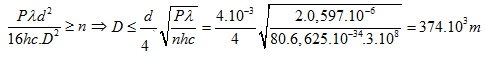
Bài 6.Thực hiện các tính toán để trả lời các câu hỏi sau
a. Electron phải có vận tốc bằng bao nhiêu để động năng của nó bằng năng lượng của một photon ánh sáng có bước sóng $\lambda =5200{{A}^{0}}$?
b. Năng lượng của photon phải bằng bao nhiêu để khối lượng của nó bằng năng lượng nghỉ của electron? Cho khối lượng nghỉ của electron là ${{m}_{e}}=9,{{1.10}^{-31}}kg$.
HD Giải :
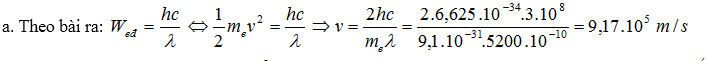
b. Năng lượng của photon:$E={{m}_{ph}}{{c}^{2}}$ Khối lượng của electron bằng khối lượng nghỉ của electron $\left( {{m}_{ph}}={{m}_{e}} \right)$ nên:
$E={{m}_{e}}{{c}^{2}}=9,{{1.10}^{-31}}.{{\left( {{3.10}^{8}} \right)}^{2}}=8,{{19.10}^{-14}}J=0,51\ MeV$
Bài 7 : Cho công thoát của đồng bằng 4,47eV.
a. Tính giới hạn quang điện của đồng?
b. Chiếu bức xạ có bước sóng $\lambda =0,14\mu m$ vào quả cầu bằng đồng đặt xa các vật khác thì quả cầu được tích đến điện thế cực đại bằng bao nhiêu? Tính vận tốc ban đầu cực đại của các electron quang điện ?
c. Chiếu bức xạ điện từ vào quả cầu bằng đồng đặt xa các vật khác thì quả cầu được tích điện đến điện thế cực đại ${{V}_{\max }}=3V$.Tính bước sóng của bức xạ đó và vận tốc ban đầu cực đại của các electron quang điện trong trường hợp này?
HD Giải :
a. ${{\lambda }_{0}}=\frac{hc}{A}={{278.10}^{-9}}m=278\ nm$
b. Theo công thức Einstein: $\frac{hc}{\lambda }=A+\frac{1}{2}mv_{0\max }^{2}$Mà điện thế cực đại của vật tính theo công thức: $\frac{1}{2}mv_{0\max }^{2}=\left| e \right|{{V}_{\max }}$
$\Rightarrow $\[\frac{hc}{\lambda }=A+\left| e \right|{{V}_{\max }}\] $\to $ ${{V}_{\max }}=\frac{\frac{hc}{\lambda }-A}{\left| e \right|}=\frac{\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{14.10}^{-6}}}-4,47.1,{{6.10}^{-19}}}{1,{{6.10}^{-19}}}=4,4\ V$
Lại có: $\frac{1}{2}mv_{0\max }^{2}=\left| e \right|{{V}_{\max }}$ $\to $ ${{v}_{0\max }}=\sqrt{\frac{2.\left| e \right|{{V}_{\max }}}{m}}=\sqrt{\frac{2.1,{{6.10}^{-19}}.4,4}{9,{{1.10}^{-31}}}}=1,{{244.10}^{6}}m/s$
c. Tương tự câu b: \[\frac{hc}{\lambda }=A+\left| e \right|V_{\max }^{'}\]$\to $ $\lambda =\frac{hc}{A+\left| e \right|V_{\max }^{'}}={{166.10}^{-9}}m=166\ nm$