KHỐI TRÒN XOAY
A.Kiến thức cần nắm :
I. Sự tạo thành của khối tròn xoay:
Trong không gian cho mặt phẳng (P) chứa đường thẳng A và chữa đường \[\Delta \]. Khi quay mặt phẳng (P) xung quanh \[\Delta \] một góc \[{{360}^{o}}\]thì ta được đường C tạo nên một khối tròn xoay. Mặt tròn xoay đó nhận \[\Delta \] làm trục, đường C được giọi là đường sinh
II. TÍNH CHẤT CỦA MẶT TRÒN XOAY
– Nếu cắt mặt tròn xoay bởi một mặt phẳng vuông góc với trục Δ ta được giao tuyến là các đường tròn có tâm trên Δ.
– Mỗi điểm M trên mặt tròn xoay đều nằm trên một đường tròn thuộc mặt tròn xoay và đường tròn này có tâm thuộc trục A.
III. MẶT NÓN TRÒN XOAY
1. Định nghĩa.
Trong mặt phẳng (P) cho hai đường thẳng Δ và d cắt nhau tại O tạo thành góc a với 0° < α < 90°. Mặt tròn xoay sinh ra bởi đường thẳng d khi quay mặt phẳng (P) xung quanh A gọi là mặt nón tròn xoay đỉnh O. Người ta thường gọi tắt mặt nón tròn xoay là mặt nón. Đường thẳng A gọi là trục, đường thẳng d gọi là đường sinh, góc 2 α gọi là góc ở đỉnh của mặt nón tròn xoay.
2. Tính chất
a) Nếu cắt mặt nón tròn xoay đỉnh o bởi mặt phẳng đi qua đỉnh O ta có các trường hợp sau đây :
– Mặt phẳng cắt mặt nón theo hai đường sinh ;
– Mặt phẳng tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này người ta gọi mặt phẳng đó là tiếp diện của mặt nón ;
– Mặt phẳng chỉ có một điểm O chung duy nhất với mặt nón, ngoài ra không có một điểm chung nào khác.
b) Nếu cắt mặt nón tròn xoay đỉnh O bởi mặt phẳng (P) không đi qua đỉnh o ta có các trường hợp sau đây :
– Nếu mặt phẳng (P) cắt mọi đường sinh của mặt nón, ta được giao tuyến là
một đường elip hoặc là một đường tròn (khi mặt phẳng (P) vuông góc với trục Δ của mặt nón); :
– Nếu mặt phẳng (P) song song với chỉ một đường sinh của mặt nón, ta được giao tuyến là một đường parabol;
– Nếu mặt phẳng (P) song song với hai đường sinh của mặt nón, ta được giao tuyến là hai nhánh của một đường hypebol.
3. Hình nón tròn xoay và khối nón tròn xoay
Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình gọi là hình nón tròn xoay (hay hình nón). Hình tròn tâm I bán kính IM gọi là mặt đáy, điểm O gọi là đỉnh, độ dài OI gọi là chiều cao và độ dài OM gọi là đường sinh của hình nón đó.
Khối nón tròn xoay (hay khối nón) là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó.
4. Diện tích xung quanh của hình nón tròn xoay
Gọi Sxq là diện tích xung quanh của hình nón có bán kính đường tròn đáy bằng r và có độ dài đường sinh bằng l.
Ta có công thức :\[{{S}_{xq}}~=~\pi rl\].
Diện tích toàn phần của hình nón tròn xoay bằng diện tích xung quanh của hình nón cộng diện tích đáy của hình nón.
5. Thể tích khối nón tròn xoay
Gọi V là thể tích của khối nón tròn xoay có chiều cao h và có diện tích đáy là B.
Ta có công thức \[V=\frac{1}{2}B.h\] . Nếu bán kính đáy bằng r ta có \[V=\frac{1}{2}\pi {{r}^{2}}h\] .
V. MẶT TRỤ TRÒN XOAY
1. Định nghĩa.
Trong mặt phẳng (P) cho hai đường thẳng A và l song song với nhau, cách nhau một khoảng bằng Khi quay mặt phẳng (P) xung quanh trục Δ thì đường thẳng l sinh ra một mặt tròn xoay gọi là mặt trụ tròn xoay và được gọi tắt là mặt trụ. Đường thẳng Δ gọi là trục của mặt trụ, đường thẳng l gọi là đường sinh của mặt trụ và r là bán kính của mặt trụ đó.
2. Tính chất
a) Nếu cắt mặt trụ tròn xoay (có bán kính bằng r) bởi một mặt phẳng (P) vuông góc với trục Δ thì ta được một đường tròn có tâm trên Δ và có bán kính bằng
b ) Nếu cắt mặt trụ tròn xoay (có bán kính bằng r) bởi một mặt phẳng ( α) không vuông góc với trục Δ, nhưng cắt tất cả các đường sinh, ta được giao tuyến là đường elip có trục nhỏ bằng 2r và trục lớn bằng 2r/sin φ trong đó φ là góc giữa trục Δ và mặt phẳng ( α ) (0° < φ < 90°).
c) Nếu M là một điểm bất kì nằm trên mặt trụ tròn xoay có trục là Δ và có bán kính r thì đường thẳng l‘ đi qua M và song song với Δ sẽ nằm trên mặt trụ đó và như vậy l’ là một đường sinh của mặt trụ đã cho.
d) Cho mặt phẳng ( α) song song với trục A của mặt trụ tròn xoay (có bán kính bằng r) và cách Δ một khoảng bằng Nếu h < r thì mặt phẳng (a) cắt mặt trụ theo hai đường sinh, nếu h = r thì mặt phẳng ( α) tiếp xúc với mặt trụ theo một đường sinh, còn nếu h> r thì mặt phẳng (à) không cắt mặt trụ.
3. Hình trụ tròn xoay và khối trụ tròn xoay
Cho hình chữ nhật ABCD. Khi quay hình chữ nhật đó xung quanh đường thẳng chứa một cạnh, ví dụ cạnh AB, thì đường gấp khúc ADCB tạo thành một hình gọi là hình trụ tròn xoay (hay hình trụ).
Khi quay quanh AB, hai cạnh AD và BC sẽ tạo ra hai hình tròn bằng nhau gọi là hai đáy của hình trụ, còn cạnh CD là đường sinh tạo ra mặt xung quanh của hình trụ. Khoảng cách AB giữa hai mặt phẳng song song chứa hai đáy là chiều cao của hình trụ.
Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó. Khối trụ tròn xoay còn được gọi tắt là khối trụ. Ta gọi mặt đáy, chiều cao, đường sinh của một khối trụ theo thứ tự là mặt đáy, chiều cao, đường sinh của hình trụ tương ứng làm giới hạn cho khối trụ đó.
4. Diện tích xung quanh của hình trụ
Nếu gọi Sxq là diện tích xung quanh của hình trụ có bán kính đáy bằng r và có đường sinh bằng l ta có công thức :
\[{{S}_{xq}}~=~2\pi rl\].
Diện tích toàn phần của hình trụ tròn xoay bằng diện tích xung quanh của hình trụ đó cộng với diện tích hai đáy của hình trụ.
5. Thể tích khối trụ
Gọi V là thể tích khối trụ tròn xoay có chiều cao h và có diện tích đáy là B. Ta có công thức V = Bh. Nếu bán kính đáy bằng r ta có
\[V=\frac{1}{2}\pi {{r}^{2}}h\] .
B.Bài tập minh họa :
Câu 1: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Hình đa diện nào sau đây không có tâm đối xứng?
A. Hình bát diện đều. B. Hình tứ diện đều. C. Hình lập phương. D. Hình hộp chữ nhật.
Lời giải
Chọn B
Câu 2: (THPT Tam Phước-Đồng Nai-lần 1-năm 2017-2018) Cho hình trụ có bán kính đáy bằng 3 cm, độ dài đường cao bằng 4 cm. Tính diện tích xung quanh của hình trụ này?
\[\text{A}\text{. 24}\pi \text{c}{{\text{m}}^{2}}\text{. B}\text{. 22}\pi \text{c}{{\text{m}}^{2}}\text{. C}\text{. 26}\pi \text{c}{{\text{m}}^{2}}\text{. D}\text{.20}\pi \text{c}{{\text{m}}^{2}}\]
Lời giải: \[{{\text{S}}_{xq}}=2\pi Rl=2\pi .3.4\]
Chọn A
Câu 3: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chóp có đáy là hình thang vuông thì luôn có mặt cầu ngoại tiếp.
B. Hình chóp có đáy là hình thoi thì luôn có mặt cầu ngoại tiếp.
C. Hình chóp có đáy là hình tứ giác thì luôn có mặt cầu ngoại tiếp.
D. Hình chóp có đáy là hình tam giác thì luôn có mặt cầu ngoại tiếp.
Lời giải:
Chọn D
Điều kiện để một hình chóp có mặt cầu ngoại tiếp là đa giác đáy là đa giác nội tiếp đường tròn.
Do đó: Đáy là tam giác thì luôn có tâm đường tròn ngoại tiếp.
Câu 4: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Tính thể tích V của khối trụ có bán kính đáy và chiều cao đều bằng 2 .
\[\text{A}\text{. 4}\pi \text{V }\text{. B}\text{. 12}\pi \text{V }\text{. C}\text{. 16}\pi \text{V }\text{. D}\text{. 8}\pi \text{V}\]
Lời giải:
Thể tích khối trụ \[\text{V=}\pi {{\text{r}}^{2}}.h=\pi {{.2}^{2}}.2=8\pi \].
Chọn D
Câu 5: (THPT Cổ Loa-Hà Nội-lần 1-năm-2018) Gọi l , h , r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh \[{{\text{S}}_{xq}}\] của hình nón là
A.\[{{\text{S}}_{xq}}=2\pi Rh\]. B.\[{{\text{S}}_{xq}}=2\pi Rl\]. C.\[{{\text{S}}_{xq}}=\pi Rl\]. D.\[{{\text{S}}_{xq}}=\frac{1}{3}\pi {{R}^{3}}\]
Lời giải: \[{{\text{S}}_{xq}}=\pi Rl\]
Chọn C
Câu 7: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Cho khối nón có bán kính đáy \[r=\sqrt{3}\]và chiều cao \[h=4\]. Tính thể tích V của khối nón đã cho.
.png)
Lời giải: Thể tích khối nón là: \[V=\frac{1}{3}{{(\sqrt{3})}^{2}}\pi .4\]
Chọn D
Câu 8: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Tính đường kính mặt cầu ngoại tiếp hình lập phương có cạnh bằng 3a
A.6a. B.\[\frac{3}{2}a\]. C.\[a\sqrt{3}\]. D.3a.
Lời giải:
Gọi O là tâm hình lập phương
Ta có các tứ giác AA’C’C , ABC’D’ và BB’D’D là các hình chữ nhật
OA=OB=OC=OD=OA’=OB’=OC’=OD’
Do đó O là tâm mặt cầu ngoại tiếp hình lập phương.
Khi đó đường kính \[\text{d=AC }\!\!'\!\!\text{ =a}\sqrt{3}.\sqrt{3}=3a\]
Chọn D
Câu 9: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Nếu cạnh của hình lập phương tăng lên gấp 2 lần thì thể tích của hình lập phương đó sẽ tăng lên bao nhiêu lần?
A. 9 . B. 8 . C. 6 . D. 4 .
Lời giải:
Ta có thể tích của hình lập phương cạnh a là\[{{a}^{3}}\].
Do đó khi tăng cạnh hình lập phương lên 2 lần thì thể tích là \[8{{a}^{3}}\].
Chọn B
Câu 10: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Cho đường thẳng l cắt và không vuông
góc với trục và khi quay quanh trục thì ta được
A. Hình nón tròn xoay. B. Mặt nón tròn xoay.
C. Khối nón tròn xoay. D. Mặt trụ tròn xoay.
Lời giải
Chọn B
Theo định nghĩa.
Câu 11: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Khối trụ tròn xoay có đường kính đáy là
2a , chiều cao là h=2a có thể tích là:
\[\text{A}\text{. }\pi {{\text{a}}^{3}}\text{. B}\text{. 2}\pi {{a}^{2}}\text{h}\text{. C}\text{. 2}\pi {{\text{a}}^{2}}\text{. D}\text{. 2}\pi {{\text{a}}^{3}}.\]
Lời giải:
Chọn D
Ta có : \[\text{V=S}\text{.h=}\pi {{\text{r}}^{2}}h=\pi {{a}^{2}}.2a=2\pi {{a}^{3}}\]
Câu 12: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Một hình trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông. Khi đó diện tích toàn phần của hình trụ đó là ?
\[\text{A}\text{. 6}\pi {{\text{r}}^{2}}\text{ B}\text{. 2}\pi {{\text{r}}^{2}}\text{ C}\text{. 8}\pi {{\text{r}}^{2}}\text{ D}\text{. 4}\pi {{\text{r}}^{2}}\]
Lời giải
Chọn A
.png)
Do thiết diện qua trục là hình vuông nên h=l=2r.
Ta có\[{{S}_{tp}}={{S}_{xq}}+2{{S}_{\text{d}}}=2\pi r.2r+2\pi {{r}^{2}}\].
Câu 13: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Công thức tính diện tích mặt cầu bán kính R là
A.\[S=\pi {{R}^{2}}\].B.\[S=\frac{4}{3}\pi {{R}^{3}}\]. C.\[S=\frac{3}{4}\pi {{R}^{3}}\]. D.\[S=4\pi {{R}^{2}}\]
Lời giải
Chọn D
Công thức tính diện tích mặt cầu bán kính R là \[S=4\pi {{R}^{2}}\]
Câu 14: (THPT Kim Liên-Hà Nội năm 2017-2018) Trong các hình đa diện sau, hình nào không nội tiếp được trong một mặt cầu?
A. Hình tứ diện. B. Hình hộp chữ nhật.
C. Hình chóp ngũ giác đều. D. Hình chóp có đáy là hình thang vuông.
Lời giải
Chọn D
Vì hình thang vuông không nội tiếp được trong một đường tròn nên hình chóp có đáy là hình
thang vuông không nội tiếp được trong một mặt cầu.
Câu 15: (THPT Kiến An-Hải Phòng năm 2017-2018) Cho hình cầu đường kính\[2a\sqrt{3}\]. Mặt phẳng (P)
cắt hình cầu theo thiết diện là hình tròn có bán kính bằng \[a\sqrt{2}\] . Tính khoảng cách từ tâm hình
cầu đến mặt phẳng (P)
A.a. B.\[\frac{a}{2}\]. C.\[\frac{a}{3}\] . D.\[\frac{a}{4}\].
Lời giải
Chọn A
.png)
Bán kính hình cầu đã cho là \[R=a\sqrt{3}\] .
Khoảng cách từ tâm hình cầu đến mặt phẳng (P) là \[d=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}-{{\left( a\sqrt{2} \right)}^{2}}}=a\].
Câu 16: (THPT Kiến An-Hải Phòng năm 2017-2018) Tính diện tích xung quanh của một hình trụ có chiều cao 20m , chu vi đáy bằng 5m .
\[\text{A}\text{.50}{{\text{m}}^{2}}\text{. B}\text{. 50}\pi {{\text{m}}^{2}}\text{. C}\text{. 100}\pi {{\text{m}}^{2}}\text{. D}\text{. 100}{{\text{m}}^{2}}\]
Lời giải
Chọn D
Ta có chu vi đáy \[C=2\pi R=5\].
Diện tích xung quanh của hình trụ là \[{{S}_{xq}}=2\pi Rl=5.20=100{{m}^{2}}\] .
Câu 17: (THPT Kiến An-Hải Phòng năm 2017-2018) Cho khối nón có chiều cao bằng 24cm, độ dài đường sinh bằng 26cm. Tính thể tích V của khối nón tương ứng.
A.\[800\pi c{{m}^{3}}\]. B.\[1600\pi c{{m}^{3}}\]. C.\[\frac{1600}{3}\pi c{{m}^{3}}\]. D.\[\frac{800}{3}\pi c{{m}^{3}}\].
Lời giải
Chọn D
Bán kính đáy của hình nón \[R=\sqrt{{{l}^{2}}-{{h}^{2}}}=10cm\].
Vậy thể tích khối nón tương ứng là:.\[V=\frac{1}{3}\pi {{R}^{2}}.h=\frac{1}{3}\pi .100.24=\frac{800}{3}\pi c{{m}^{3}}\]
C.Bài tập tự luyện:
Câu 1: Mặt phẳng chứa trục của một hình nón cắt hình nón theo thiết diện là:
A. một hình chữ nhật. B. một tam giác cân. C. một đường elip. D. một đường tròn.
Câu 2: Một hình trụ có bán kính đáy 5cm , chiều cao 7cm . Tính diện tích xung quang của hình trụ.
A.\[\text{S=25}\pi \text{c}{{\text{m}}^{2}}\] B.\[\text{S=70}\pi \text{c}{{\text{m}}^{2}}\] C.\[\text{S=75}\pi \text{c}{{\text{m}}^{2}}\] D.\[\text{S=100}\pi \text{c}{{\text{m}}^{2}}\]
Câu 3:Gọi r là bán kính đường tròn đáy và l là độ dài đường sinh của hình trụ. Diện tích xung quanh của hình trụ là ?
A.\[2\pi {{r}^{2}}l\]. B.\[\pi rl\]. C.\[2\pi rl\] D.\[\frac{1}{3}\pi rl\]
Câu 4: Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a . Diện tích xung quanh của hình nón bằng
A.\[\frac{\pi {{a}^{2}}\sqrt{2}}{4}\] B.\[\frac{\pi {{a}^{2}}\sqrt{2}}{3}\] C.\[\frac{\pi {{a}^{2}}\sqrt{2}}{2}\] D.\[\frac{\pi {{a}^{2}}\sqrt{3}}{2}\]
Câu 5:Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền bằng \[\sqrt{2}a\] . Tính diện tích xung quanh \[{{S}_{xq}}\]của hình nón đó.
A.\[{{S}_{xq}}~=\frac{\pi {{a}^{2}}\sqrt{3}}{3}\] B.\[{{S}_{xq}}~=\frac{\pi {{a}^{2}}\sqrt{2}}{2}~\] C.\[{{S}_{xq}}~=\frac{\pi {{a}^{2}}\sqrt{2}}{6}\] D.\[{{S}_{xq}}~=\frac{\pi {{a}^{2}}\sqrt{2}}{8}\]
Câu 6:Cho hình trụ có bán kính đáy bằng R và chiều cao bằng \[\frac{3R}{2}\]. Mặt phẳng \[\left( \alpha \right)\] song song với trục của hình trụ và cách trục một khoảng bằng \[\frac{R}{2}\] . Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng \[\left( \alpha \right)\].
A.\[\frac{3{{R}^{2}}\sqrt{3}}{2}\] B.\[\frac{3{{R}^{2}}\sqrt{3}}{3}\] C.\[\frac{2{{R}^{2}}\sqrt{3}}{3}\] D.\[\frac{2{{R}^{2}}\sqrt{2}}{3}\]
Câu 7:Cho hình trụ có tỉ số diện tích xung quanh và diện tích toàn phần bằng \[\frac{1}{3}\]. Biết thể tích khối trụ bằng \[4\pi \]. Bán kính đáy của hình trụ là
A.\[\sqrt{2}\] B.\[\sqrt{3}\] C.3 D.2
Câu 8: Cắt hình nón S bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân, cạnh huyền bằng \[a\sqrt{2}\] . Thể tích khối nón bằng:
A.\[\frac{\pi a\sqrt{3}}{2}\] B.\[\frac{\pi a\sqrt{3}}{6}\] C.\[\frac{\pi a\sqrt{2}}{6}\] D.\[\frac{\pi a\sqrt{2}}{12}\]
Câu 9: Cho tam giác ABC vuông cân tại A , trung điểm của BC là điểm O , AB=2a . Quay tam giác ABC quanh trục OA . Diện tích xung quanh của hình nón tạo ra bằng:
A.\[2\sqrt{2}\pi a\] B. \[\frac{2\sqrt{2}}{3}\pi a\] C. \[2\sqrt{2}\pi {{a}^{2}}\] D.\[\frac{2\sqrt{2}}{3}\pi {{a}^{^{2}}}\]
Câu 10: Viện Hải dương học dự định làm một bể cá bằng kính phục vụ khách tham quan (như hình vẽ), biết rằng mặt cắt dành cho lối đi là nửa hình tròn
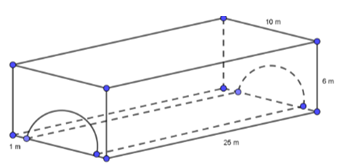
Tổng diện tích mặt kính của bể cá gần nhất với số nào sau đây?
A. 872\[{{m}^{2}}\] . B. 914\[{{m}^{2}}\] . C. 984\[{{m}^{2}}\]. D. 949\[{{m}^{2}}\]
.png)







