Mặt trụ, hình trụ, khối trụ
I/ Lý thuyết
1/ Định nghĩa: Cho đường thẳng $\Delta $. Một đường thẳng l song song với $\Delta $ và cách $\Delta $ một khoảng không đổi R. Mặt tròn xoay sinh bởi đường thẳng l khi quay quanh $\Delta $ gọi là mặt trụ tròn xoay (hay đơn giản là mặt trụ).
$\Delta $: trục của mặt trụ.
l : đường sinh của mặt trụ.
R : bán kính của mặt trụ.
2/ Hình trụ và khối trụ:
a/ Hình trụ: Cho mặt trụ có trục $\Delta $, đường sinh l và bán kính R.
Cắt mặt trụ bởi 2 mặt phẳng $\left( P \right)$ và $\left( P' \right)$ cùng vuông góc với $\Delta $ ta được thiết diện là hai đường tròn (C ) và (C’ ).
Khi đó phần của mặt trụ giới hạn bởi hai mặt phẳng $\left( P \right)$ và $\left( P' \right)$ cùng với hai đường tròn (C ) và (C’ ) được gọi là hình trụ.
b/ Khối trụ: Là phần không gian giới hạn bởi hình trụ, kể cả hình trụ đó.
3/ Diện tích hình trụ và thể tích khối trụ:
Cho hình trụ có chiều cao h, đường sinh l và bán kính đáy R.
- Diện tích xung quanh của hình trụ
${{S}_{xq}}=2\pi Rl$
- Thể tích khối trụ
$V=\pi {{R}^{2}}h$
II/ Bài tập
1/ Bài tập có hướng dẫn
Câu 1. Cho hình trụ (T) có chiều cao h, độ dài đường sinh $l$, bán kính đáy r. Ký hiệu ${{S}_{xq}}$ là diện tích xung quanh của (T). Công thức nào sau đây là đúng?
A. ${{S}_{xq}}=\pi rh$ B. ${{S}_{xq}}=2\pi rl$ C. ${{S}_{xq}}=2\pi {{r}^{2}}h$ D. ${{S}_{xq}}=\pi rl$
Với hình trụ ta có $h=l\Rightarrow {{S}_{xq}}=2\pi rh=2\pi rl$. Chọn D
Câu 2. Cho hình trụ (T) có chiều cao h, độ dài đường sinh $l$, bán kính đáy r. Ký hiệu ${{S}_{tp}}$ là diện tích toàn phần của (T). Công thức nào sau đây là đúng?
A. ${{S}_{tp}}=\pi rl$ B. ${{S}_{tp}}=\pi rl+2\pi r$ C. ${{S}_{tp}}=\pi rl+\pi {{r}^{2}}$ D. ${{S}_{tp}}=2\pi rl+2\pi {{r}^{2}}$
Ta có: ${{S}_{tp}}={{S}_{xq}}+{{S}_{2.d}}=2\pi rh+2\left( \pi {{r}^{2}} \right)=2\pi rl+2\pi {{r}^{2}}$. Chọn D
Câu 3. Cho hình trụ (T) có chiều cao h, độ dài đường sinh $l$, bán kính đáy r. Ký hiệu ${{V}_{\left( T \right)}}$ là thể tích khối trụ (T). Công thức nào sau đây là đúng?
A. ${{V}_{\left( T \right)}}=\frac{1}{3}\pi rh$ B. ${{V}_{\left( T \right)}}=\pi {{r}^{2}}h$ C. ${{V}_{\left( N \right)}}=\pi r{{l}^{2}}$ D. ${{V}_{\left( N \right)}}=2\pi {{r}^{2}}h$
Ta có: ${{V}_{\left( T \right)}}={{S}_{d}}.h=\pi {{r}^{2}}h$. Chọn B
Câu 4. Một hình trụ có bán kính đáy $r=5cm$, chiều cao $h=7cm$ . Diện tích xung quanh của hình trụ này là:
A. $35\pi \left( c{{m}^{2}} \right)$ B. $70\pi \left( c{{m}^{2}} \right)$ C. $\frac{70}{3}\pi \left( c{{m}^{2}} \right)$ D. $\frac{35}{3}\pi \left( c{{m}^{2}} \right)$
Ta có: ${{S}_{xq}}=2\pi rh=2\pi .5.7=70\pi \left( c{{m}^{2}} \right)$. Chọn B
Câu 5. Một hình trụ có bán kính đáy $r=a$, đồ dài đường sinh $l=2a$ . Diện tích toàn phần của hình trụ này là:
A. $6\pi {{a}^{2}}$ B. $2\pi {{a}^{2}}$ C. $4\pi {{a}^{2}}$ D. $5\pi {{a}^{2}}$
Ta có: ${{S}_{tp}}={{S}_{xq}}+{{S}_{2.d}}=2\pi rh+2\left( \pi {{r}^{2}} \right)=2\pi rl+2\pi {{r}^{2}}=4{{a}^{2}}\pi +2{{a}^{2}}\pi =6{{a}^{2}}\pi $. Chọn A
Câu 6. Cho hình chữ nhật ABCD có $AB=a$ và góc $BDC={{30}^{0}}$ . Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:
A. $\sqrt{3}\pi {{a}^{2}}$ B. $2\sqrt{3}\pi {{a}^{2}}$ C. $\frac{2}{\sqrt{3}}\pi {{a}^{2}}$ D. $\pi {{a}^{2}}$
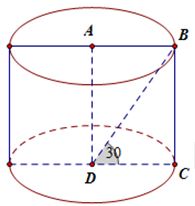Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ như hình vẽ. Ta có: $r=AB=a;h=BC=CD\tan {{30}^{0}}$ .
Suy ra $h=\frac{a}{\sqrt{3}}\Rightarrow {{S}_{xq}}=2\pi rh=\frac{2\pi {{a}^{2}}}{\sqrt{3}}$.
Chọn C
Câu 7. Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng $30c{{m}^{2}}$ và chu vi bằng $26cm$ . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ (T). Diện tích toàn phần của (T) là:
A. $\frac{69\pi }{2}\left( c{{m}^{2}} \right)$ B. $69\pi \left( c{{m}^{2}} \right)$ C. $23\pi \left( c{{m}^{2}} \right)$ D. $\frac{23\pi }{2}\left( c{{m}^{2}} \right)$
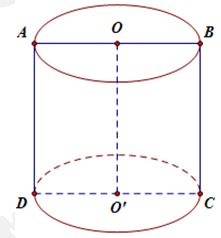Giả sử thiết diện là hình chữ nhật ABCD như hình vẽ khi đó \[AD>CD\] .
.png)
Với $AD>CD$giải hệ trên ta được $AD=10=h;CD=3=2r$ $\Rightarrow r=\frac{3}{2}$ . Khi đó ${{S}_{tp}}=2\pi rh+2\pi {{r}^{2}}=2\pi \frac{3}{2}.10+2\pi \frac{9}{4}=\frac{69\pi }{2}\left( c{{m}^{2}} \right)$
Chọn A
Câu 8. Cho hình vuông ABCD có cạnh 2 cm, biết O và O’ lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh trục OO’ thì khối trụ tròn xoay được tạo thành có thể tích bằng:
A. $2\pi \left( c{{m}^{3}} \right)$ B. \[4\pi \left( c{{m}^{3}} \right)\] C. \[6\pi \left( c{{m}^{3}} \right)\] D. \[8\pi \left( c{{m}^{3}} \right)\]
Thể tích của hình trụ là $V=\pi {{r}^{2}}h=\pi {{.1}^{2}}.2=2\pi $. Chọn A
Câu 9. Cho lăng trụ tam giác đều có tất cả các cạnh bằng $a$ . Một hình trụ tròn xoay có hai đáy là hai hình tròn ngoại tiếp hai đáy của lăng trụ. Thể tích của khối trụ tròn xoay bằng:
A. $\pi {{a}^{3}}$ B. $\frac{\pi {{a}^{3}}}{9}$ C. $3\pi {{a}^{3}}$ D. $\frac{\pi {{a}^{3}}}{3}$
Gọi R, h là bán kính đáy và chiều cao của hình trụ. Ta có $h=a$ (cùng đường cao với lăng trụ) là $R=\frac{a\sqrt{3}}{3}$ vì R cũng là bán kính đường tròn ngoại tiếp đáy lăng trụ $\Rightarrow V=\pi {{R}^{2}}h=\frac{\pi {{a}^{3}}}{3}$. Chọn D
Câu 10. Trong một chiếc hộp hình trụ người ta bỏ vào đó ba quả banh tennis, biết rằng đáy của hình trụ bằng hình tròn lớn trên quả banh và chiều cao của hình trụ bằng 3 lần đường kính của quả banh. Gọi ${{S}_{1}}$ là tổng diện tích của ba quả banh và ${{S}_{2}}$ là diện tích xung quanh của hình trụ. Tỉ số $\frac{{{S}_{1}}}{{{S}_{2}}}$ bằng:
A. 1 B. 2 C. 3 D. $\frac{1}{2}$
Gọi R là bán kính 1 quả banh $\Rightarrow $ Tổng diện tích 3 quả banh: ${{S}_{1}}=3\times 4\pi {{R}^{2}}=12\pi {{R}^{2}}$
Chiếc hộp có bán kính đáy cũng bằng R và chiều cao bằng $h=6R$
$\Rightarrow $ Diện tích xung quanh hình trụ ${{S}_{2}}=2\pi Rh=12\pi {{R}^{2}}\Rightarrow \frac{{{S}_{1}}}{{{S}_{2}}}=1$ .Chọn A
2/ Bài tập tự luyện
Câu 1. Quay hình vuông ABCD cạnh $a$ xung quanh một cạnh. Thể tích của khối trụ được tạo thành là:
A. $\frac{1}{3}\pi {{a}^{3}}$ B. $2\pi {{a}^{3}}$ C. $\pi {{a}^{3}}$ D. $3\pi {{a}^{3}}$
Câu 2. Cho hình vuông ABCD cạnh 8cm. Gọi M, N lần lượt là trung điểm của $AB$ và $CD$ . Quay hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là:
A. $64\pi \left( c{{m}^{2}} \right)$ B. $32\pi \left( c{{m}^{2}} \right)$ C. $96\pi \left( c{{m}^{2}} \right)$ D. $126\pi \left( c{{m}^{2}} \right)$
Câu 3. Một hình trụ (T) có diện tích toàn phần là $120\pi \left( c{{m}^{2}} \right)$ và có bán kính đáy bằng 6cm. Chiều cao của (T) là:
A. 6cm B. 5cm C. 4cm D. 3cm
Câu 4. Một khối trụ (T) có thể tích bằng $81\pi \left( c{{m}^{3}} \right)$ và có dường sinh gấp ba lấn bán kính đáy. Độ dài đường sinh của (T) là:
A. 12cm B. 3cm C. 6cm D. 9cm
Câu 5. Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm được thiết diện là một hình vuông có diện tích bằng $16c{{m}^{2}}$ . Thể tích của (T) là:
A. $32\pi \left( c{{m}^{3}} \right)$ B. $16\pi \left( c{{m}^{3}} \right)$ C. $64\pi \left( c{{m}^{3}} \right)$ D. $8\pi \left( c{{m}^{3}} \right)$
Câu 6. Một hình trụ có tỉ số giữa diện tích toàn phần và diện tích xung quanh bằng 4. Khẳng định nào sau đây là đúng :
A. Đường sinh bằng bán kính đáy. B. Bán kính đáy bằng ba lần đường sinh
C. Đường sinh bằng ba lần bán kính đáy D. Đường sinh bằng bốn lần bán kính đáy
Câu 7. Trong không gian, cho hình chữ nhật ABCD có $AB=1$ và $AD=2$. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần ${{S}_{tp}}$ của hình trụ đó.
A. ${{S}_{tp}}=4\pi $ B. ${{S}_{tp}}=2\pi $ C. ${{S}_{tp}}=6\pi $ D. ${{S}_{tp}}=10\pi $
Câu 8. Khi quay hình chữ nhật ABCD quanh đường thẳng AB thì hình chữ nhật ABCD tạo thành hình tròn xoay là:
A. Hình trụ B. Khối trụ C. Mặt trụ D. Hai hình trụ
Câu 9. Khối nón có chiều cao $h=3cm$ và bán kính đáy $r=2cm$ thì có thể tích bằng:
A. $4\pi \left( c{{m}^{3}} \right)$ B. $\frac{4}{3}\pi \left( c{{m}^{3}} \right)$ C. $16\pi \left( c{{m}^{2}} \right)$ D. $4\pi \left( c{{m}^{2}} \right)$
Câu 10. Khối trụ có chiều cao $h=3cm$ và bán kính đáy $r=2cm$ thì có thể tích bằng:
A. $12\pi \left( c{{m}^{3}} \right)$ B. $4\pi \left( c{{m}^{3}} \right)$ C. $6\pi \left( c{{m}^{3}} \right)$ D. $12\pi \left( c{{m}^{2}} \right)$
Câu 11. Diện tích xung quanh của hình trụ có bán kính bằng 7 và chiều cao bằng 9 là:
A. $62\pi $ B. $63\pi $ C. $126\pi $ D. $128\pi $
Câu 12. Hình trụ có bán kính bằng 5, khoảng cách giữa hai đáy bằng 7. Diện tích toàn phần của hình trụ bằng:
A. $10\pi $ B. $85\pi $ C. $95\pi $ D. $120\pi $
Câu 13. Một hình trụ có bán kính đáy bằng $2cm$ , thiết diện qua trục là hình vuông. Thể tích của khối trụ tương ứng bằng:
A. $12\pi \left( c{{m}^{2}} \right)$ B. $16\pi \left( c{{m}^{2}} \right)$ C. $20\pi \left( c{{m}^{2}} \right)$ D. $24\pi \left( c{{m}^{2}} \right)$
Câu 14. Hình trụ có bán kính đáy R, thiết diện qua trục là hình vuông. Thể tích của khối lăng trụ tứ giác đều có hai đáy nội tiếp trong hai đường tròn đáy của hình trụ bằng:
A. $2{{R}^{3}}$ B. $3{{R}^{3}}$ C. $4{{R}^{3}}$ D. $5{{R}^{3}}$
Câu 15. Khối trụ có chiều cao $2a\sqrt{3}$ , bán kính đáy $a\sqrt{3}$ . Thể tích khối cầu ngoại tiếp khối trụ bằng:
A. $8\pi {{a}^{3}}\sqrt{6}$ B. $6\pi {{a}^{3}}\sqrt{3}$ C. $\frac{4\pi {{a}^{3}}\sqrt{6}}{3}$ D. $4\pi {{a}^{3}}\sqrt{3}$
Câu 16. Một hình tứ diện đều ABCD cạnh $a$ . Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác ABC và có chiều cao bằng chiều cao hình tứ diện. Diện tích xung quanh của hình trụ đó bằng:
A. $\frac{\pi {{a}^{2}}\sqrt{3}}{3}$ B. $\frac{\pi {{a}^{2}}\sqrt{2}}{2}$ C. $\frac{\pi {{a}^{2}}\sqrt{2}}{3}$ D. $\frac{\pi {{a}^{2}}\sqrt{3}}{2}$
Câu 17. Một hình trụ có bán kính đáy bằng $a$ , chiều cao \[OO'=a\sqrt{3}\] . Hai điểm A, B lần lượt nằm trên 2 đáy (O), (O’) sao cho góc giữa OO’ và AB bằng ${{30}^{0}}$. Khoảng cách giữa AB và OO’ bằng:
A. $\frac{a\sqrt{3}}{3}$ B. $\frac{a\sqrt{3}}{2}$ C. $\frac{2a\sqrt{3}}{3}$ D. $a\sqrt{3}$
Câu 18. Một hình trụ có bán kính đáy bằng chiều cao và bằng $a$ . Một hình vuông ABCD có AB, CD lần lượt là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng:
A. $\frac{5{{a}^{2}}}{2}$ B. $5{{a}^{2}}$ C. $\frac{5{{a}^{2}}\sqrt{2}}{2}$ D. $5{{a}^{2}}\sqrt{2}$
Câu 19. Hình trụ có bán kính đáy 3cm và khoảng cách giữa hai đáy bằng 10cm thì có diện tích toàn phần là:
A. $78\pi \left( c{{m}^{2}} \right)$ B. $60\pi \left( c{{m}^{2}} \right)$ C. $18\pi \left( c{{m}^{2}} \right)$ D. $69\pi \left( c{{m}^{2}} \right)$
Câu 20. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng $a$. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A’B’C’D’. Diện tích S là:
A. $\pi {{a}^{2}}$ B. $\pi {{a}^{2}}\sqrt{2}$ C. $\pi {{a}^{2}}\sqrt{3}$ D. $\frac{\pi {{a}^{2}}\sqrt{2}}{2}$
|
1. C |
2. A |
3. C |
4. D |
5. A |
6. B |
7. A |
8.A |
9. A |
10. D |
|
11.C |
12. D |
13. B |
14. C |
15. A |
16. C |
17. B |
18. A |
19. A |
20. B. |
