Bài 1: Cho hình vẽ biết \[\widehat{BAC}+\widehat{ACD}={{180}^{0}}\],\[\widehat{ADC}={{40}^{0}}\],\[\widehat{BAC}={{130}^{0}}\].Chứng minh \[AD\bot AC\]
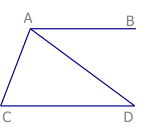
Bài 2: Cho hình vẽ biết \[\widehat{ACx}=a,\widehat{CBy}=b,\widehat{ACB}=a+b\]. Chững minh Ax song song với By
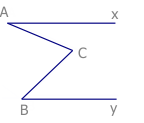
Bài 3: Cho hình vẽ biết \[\widehat{yBC}=\widehat{ACB}+\widehat{xAC}\].Chững minh rằng Ax song song với By
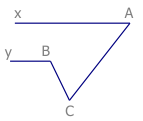
Bài 4: Cho hình vẽ biết \[\widehat{xAB}+\widehat{ABC}+\widehat{BCy}={{360}^{0}}\]. Chứng minh Ax song song với Cy
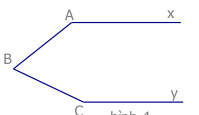
Bài 5: Cho hình biết \[\widehat{xAC}+\widehat{yBC}-\widehat{ABC}={{180}^{0}}\]. Chứng minh Ax song song By
Bài 6: Cho hình biết \[\widehat{ACB}>\widehat{xAC}\]. Chứng minh \[\widehat{ACB}=\widehat{xAC}+\widehat{CBy}\]
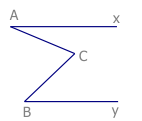
Bài 7: Cho hình biết Ax song song By. Chứng minh \[\widehat{yBC}=\widehat{ACB}+\widehat{xAC}\]
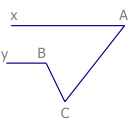
Bài 8: Cho hình biết Ax song song Cy và \[\widehat{xAC}+\widehat{ABC}>{{180}^{0}}\].Chứng minh \[\widehat{xAB}+\widehat{ABC}+\widehat{BCy}={{360}^{0}}\]
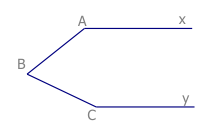
Bài 9: Cho hình biết Ax song song By và \[\widehat{ACB}<\widehat{yBC}\]. Chứng minh \[\widehat{xAC}+\widehat{yBC}-\widehat{ACB}={{180}^{0}}\]
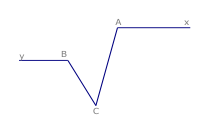
Bài 10: Cho 5 đường thẳng trên mặt phẳng trong đó không có hai đường thẳng nào song song .Chứng minh rằng tồn tai hai đường thẳng tạo với nhau góc nhỏ hơn hoặc bằng 360.
Bài 11: Cho một góc mà đỉnh của nó không có trong hình vẽ và điểm M nằm trong góc đó. Qua điểm M hãy dựng đường thẳng vuông góc với tia phân giác của góc đã cho .
Bài 12: Chứng minh rằng hai góc nhon ( tù ) có cạnh vuông góc với nhau từng đôi một thì bằng nhau .
Bài 13: Cho một đường thẳng cắt hai đường thẳng song song. Chứng minh rằng :
a) Các tia phân giác của một cặp góc so le trong ( hoặc so le ngoài ) thì song song với nhau.
b) Các tia phan giác của một cặp góc đồng vị thì song song với nhau.
c) Các tia phân giác của một cặp góc trong cùng phía (hoặc ngoài cùng phía ) thì vuông góc với nhau
.PNG)







