Ví dụ 1: Cho \[\Delta \]ABC có 3 góc nhọn (AB < AC), M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho BM = MD.
a) Chứng minh \[\Delta \]ABM = \[\Delta \]CDM
b) Chứng minh AB // CD.
c) Vẽ AH, CK vuông góc với BD (K, H thuộc BD). Chứng minh BH = DK
Giải.
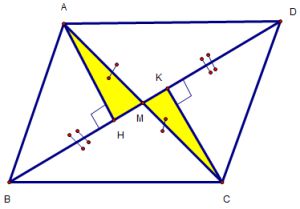
a) Chứng minh : \[\Delta \]ABM = \[\Delta \]CDM
Xét \[\Delta \]ABM và \[\Delta \]CDM :
MA = MC (gt)
MB = MD (gt)
\[\Rightarrow \]\[\widehat{AMB}=\widehat{DMC}\] (đối đinh)
\[\Delta \]ABM = \[\Delta \]CDM (c – g – c)
b) Chứng minh : AB // CD
Ta có :
\[\widehat{ABM}=\widehat{MDC}\] (góc tương ứng của \[\Delta \]ABM = \[\Delta \]CDM)
Mà : \[\widehat{ABM}\];\[\widehat{MDC}\] ở vị trí so le trong
Nên : AB // CD
c) Chứng minh BK = DH
Xét \[\Delta \]ABH và \[\Delta \]CDK, ta có :
\[\widehat{H}=\widehat{K}={{90}^{0}}\]
\[\widehat{ABH}=\widehat{KDC}\] (cmt)
AB = CD (\[\Delta \]ABM = \[\Delta \]CDM)
=> \[\Delta \]ABH = \[\Delta \]CDK (cạnh huyền – góc nhọn)
=> BH = CK (cạnh tương ứng)
Ví dụ 2:
Cho \[\Delta \]ABC vuông tại A, có góc B = 550
a) Tính số đo của góc ACB
b) Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Chứng minh: \[\Delta \]ABC = \[\Delta \]ABD.
c) Từ D vẽ đường thẳng song song với BC và cắt tia BA tại E. Chứng minh:
\[\Delta \]DAB = \[\Delta \]DAE.
d) Qua C vẽ đường thẳng a vuông góc với AC và cắt tia DE tại K. Chứng minh E là trung điểm của đoạn thẳng DK.
Giải.
a) Tính góc ACB :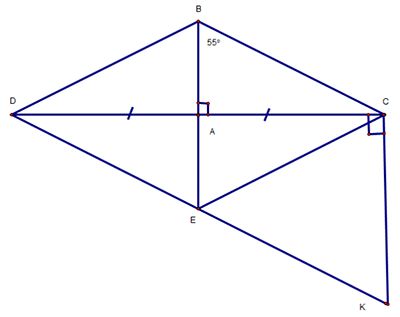
trong tam giác ABC, ta có :
\[\widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}}\]
\[\Rightarrow \widehat{C}={{180}^{0}}-({{90}^{0}}+{{55}^{0}})\]
\[\Rightarrow \] \[\widehat{C}\]=350
b) cm : \[\Delta \]ABC = \[\Delta \]ABD
Xét \[\Delta \]ABC và \[\Delta \]ABD, ta có :
\[\widehat{BAC}=\widehat{DAB}={{90}^{0}}\]
AB cạnh chung.
AC = AD (gt)
=> \[\Delta \]ABC = \[\Delta \]ABD (cạnh huyền – cạnh góc vuông)
c) cm : \[\Delta \]DAB = \[\Delta \]DAE
ta có :
\[\widehat{ADB}=\widehat{ACB}\] (\[\Delta \]ABC = \[\Delta \]ABD)
\[\widehat{ADE}=\widehat{ACB}\] (so le trong)
\[\Rightarrow \]\[\widehat{ADB}=\widehat{ADE}\]
Xét \[\Delta \]DAB VÀ \[\Delta \]DAE, ta có :
\[\widehat{DAB}=\widehat{EAD}={{90}^{0}}\]
\[\widehat{ADB}=\widehat{ADE}\] (cmt)
AD cạnh chung
=> \[\Delta \]DAB = \[\Delta \]DAE (cạnh góc vuông – góc nhọn)
d) E là trung điểm DK
Xét \[\Delta \]CAB VÀ \[\Delta \]DAE, ta có :
\[\widehat{CAB}=\widehat{EAD}={{90}^{0}}\]
\[\widehat{ADE}=\widehat{ACB}\] (so le trong)
AB = AE (\[\Delta \]DAB = \[\Delta \]DAE)
\[\Rightarrow \] \[\Delta \]CAB = \[\Delta \]DAE
\[\Rightarrow \] DE = BC (1)
TA CÓ : AE vuông góc AC (gt) và KC vuông góc AC (gt)
\[\Rightarrow \] AE // CK
\[\Rightarrow \] \[\widehat{BEC}=\widehat{KCE}\] (so le trong)
Xét \[\Delta \]CEB VÀ \[\Delta \]EKC, ta có :
\[\widehat{BEC}=\widehat{KCE}\] (cmt)
EC cạnh chung
\[\widehat{BCE}=\widehat{KEC}\] (so le trong)
\[\Rightarrow \] \[\Delta \]CEB = \[\Delta \]EKC (g – c – g)
\[\Rightarrow \] KE = BC (2)
từ (1) và (2), ta có :
DE = BC (cmt) và KE = BC (cmt)
=> DE = EK
hay E là trung điểm DK







