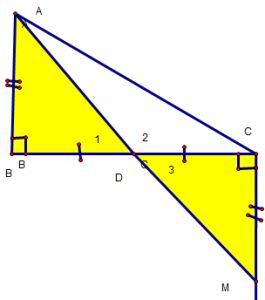
Ví dụ 1 : Cho D ABC vuông tại B. Trên nữa mặt phẳng bờ BC không có điểm A, vẽ tia Cx vuông góc BC. Trên tia Cx lấy M sao cho CM = AB. Chứng minh A, M và D là trung điểm của BC thẳng hàng.
Giải:
Xét \[\Delta ABD\]và \[\Delta MCD\] ta có:
\[\widehat{B}=\widehat{C}={{90}^{0}}\]
AB = CM (gt)
DB = DC ( D là trung điểm của BC)
\[\Rightarrow \Delta ABD=\Delta MCD\]
\[\Rightarrow \widehat{{{D}_{1}}}=\widehat{{{D}_{3}}}\]
Mặt khác : \[\widehat{{{D}_{1}}}+\widehat{{{D}_{2}}}={{180}^{0}}\] ( B, D, C thẳng hàng)
\[\Rightarrow \widehat{{{D}_{2}}}+\widehat{{{D}_{3}}}={{180}^{0}}\]
Hay : \[\widehat{ADM}={{180}^{0}}\]
\[\Rightarrow \] A, D, M thẳng hàng ( góc bẹt)
Nhận xét: Ở bài này chứng minh 3 điểm thẳng hàng bằng cách chứng minh cho góc tạo bởi 3 điểm đó là 180 độ.
Ví dụ 2: Cho tam giác ABC. Gọi D, E lần lượt là trung điểm của AB, AC. Trêm tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. Chứng minh: A là trung điểm của MN
Giải:
Xét \[\Delta BCD\] và \[\Delta BMD\], ta có:
DB = DA ( D là trung điểm của AB)
\[\Rightarrow \widehat{{{D}_{1}}}=\widehat{{{D}_{2}}}\]( đối đỉnh)
DC = DM (gt)
\[\Rightarrow \Delta BCD=\Delta BMD\] (c.g.c)
\[\Rightarrow \widehat{{{C}_{1}}}=\widehat{M}\] và BC = AM
Mà: \[\widehat{{{C}_{1}}}\];\[\widehat{M}\] ở vị trí so le trong \[\Rightarrow \] BC // AM.
Chứng minh tương tự,
ta được : BC // AN và BC = AN.
ta có : BC // AM (cmt) và BC // AN (cmt)
\[\Rightarrow \]A, M. N thẳng hàng. (1)
BC = AM và BC = AN \[\Rightarrow \]AM = AN (2).
Từ (1) và (2), suy ra : A là trung điểm của MN.
Nhận xét: Chứng minh 3 điểm A, M, N thẳng hàng trước, sau đó chứng minh AM = AN
Ví dụ 3 :
Cho tam giác ABC vuông góc tại A có góc B = 530
a) Tính góc C.
b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. \[\Delta BEA\] = \[\Delta BED\]
c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. cm :\[\Delta BHF\]=\[\Delta BHC\]
d) Cmr \[\Delta BAC\]= \[\Delta BDF\] và D, E, F thẳng hàng.
Giải:
a)
Xét \[\Delta BAC\], ta có:
\[\widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}}\]
\[\Rightarrow \widehat{C}={{180}^{0}}-(\widehat{A}+\widehat{B})\]
\[\Rightarrow \widehat{C}={{180}^{0}}-({{90}^{0}}+{{53}^{0}})={{37}^{0}}\]
b) Xét \[\Delta BEA\] và \[\Delta BED\], ta có :
BE cạnh chung
\[\widehat{ABE}=\widehat{DBE}\](BE là tia phân giác của góc B)
BD = BA (gt)
\[\Rightarrow \]\[\Delta BEA=\Delta BED\](c.g.c)
c)
Xét \[\Delta BHF\]và \[\Delta BHC\], ta có:
BH cạnh chung
\[\widehat{ABH}=\widehat{DBH}\]
\[\widehat{BHF}=\widehat{BHC}\]=900(gt)
\[\Rightarrow \]\[\Delta BHF=\Delta BHC\]( cạnh huyền – góc nhọn)
\[\Rightarrow \]BF = BC
d) Xét \[\Delta BAC\] và \[\Delta BDF\], ta có:
BC = BF (cmt)
Góc B chung
BA = BC(gt)
\[\Rightarrow \]\[\Delta BAC=\Delta BDF\]
\[\Rightarrow \]\[\widehat{BAC}=\widehat{BDF}\]
Mà \[\widehat{BAC}\]= 900
Nên \[\widehat{BDF}\]= 900 hay \[BD\bot DF\](1)
Mặt khác : \[\widehat{BAE}=\widehat{BDF}\]
Mà \[\widehat{BAE}\] = 900
Nên \[\widehat{BDE}={{90}^{0}}\] hay \[BD\bot DE\](2)
Từ (1) và (2) suy ra DE trùng DF
Hay D,E,F thẳng hàng
Bài tập tự giải:
Ví dụ 1 : Cho tam giác ABC . Trên tia đối của tia AB lấy điểm F sao cho AB = FA. Trên tia đối của tia AC lấy điểm E sao cho AC = AE.
a) Chứng minh: \[\Delta EAF\] = \[\Delta CAB\]
b)Gọi K là trung điểm EF và D là trung điểm BC. Chứng minh : KB = FD.
d) Chứng minh: K, A, D thẳng hàng.
Ví dụ 2 :Cho \[\Delta \] ABC có M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D sao cho MD = MC.
a) Chứng minh \[\Delta \]MAD = \[\Delta \]MBC và AD // CB.
b) Lấy N thuộc AD; NM cắt BC tại P. Chứng minh AN = BP.
c) Trên nửa mặt phẳng bờ AB không chứa điểm D, vẽ tia AE sao cho góc EAB + góc ABC = 1800 . Chứng tỏ D, A, E thẳng hàng.







