PHÉP ĐỐI XỨNG TÂM
A/ LÝ THUYẾT
I/ Định nghĩa
+ Cho một điểm
I, phép biến hình biến điểm I thành chính nó, biến mỗi điểm khác I thành M’ sao
cho I là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm I
Ví dụ:
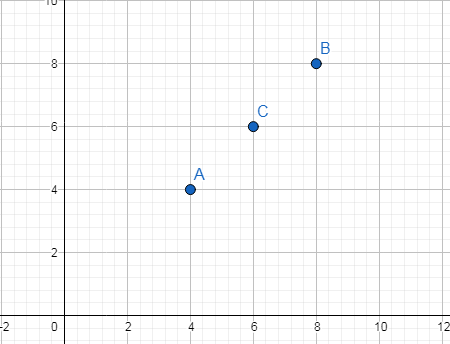
Điểm $B\left( 8;8 \right)$ là ảnh của điểm $A\left( 4;4 \right)$ qua phép đối xứng tâm $C\left( 6;6 \right)$
+ Kí hiệu: $M'={{D}_{I}}\left(
M \right)$
+ Nếu điểm
M’ là ảnh của điểmm M qua phép đối xứng tâm I thì:
$\overrightarrow{IM}+\overrightarrow{IM'}=0$
II/ Biểu thức tọa độ
Trong mặt phẳng
tọa độ cho điểm $I\left( a;b \right)$ . Nếu phép đối xứng tâm I biến điểm $M\left(
x;y \right)$ thành điểm $M'\left( x';y' \right)$ thì:
$\left\{
\begin{matrix}
x'=2a-x
\\
y'=2b-y
\\
\end{matrix}
\right.$
Chứng minh:
Thật vậy,
$\overrightarrow{IM}+\overrightarrow{IM'}=0$
Nên $\left(
x-a;y-b \right)+\left( x'-a;y'-b \right)=\left( 0;0 \right)$
$\Rightarrow
\left( x+x'-2a;y+y'-2b \right)=\left( 0;0 \right)$
$\Rightarrow
x';y'$
III/ Tâm đối xứng của một
hình
Là điểm I
sao cho phép đối xứng tâm I biến hình H thành chính nó
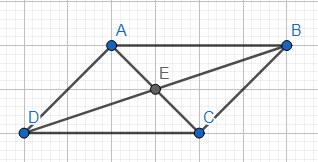
Ví dụ: Hình bình hành có tâm đối xứng là giao điểm hai đường chéo
B/ VÍ DỤ
VD 1: Trong mặt phẳng Oxy cho đường thẳng $\left(
d \right):x+y+1=0$ . Ảnh của đường thẳng d qua phép đối xứng tâm O có phương
trình:
A.$-x-y+1=0$
B.$-x+y+1=0$
C.$x-y+1=0$
D.$-x-y-1=0$
Giải:
Mỗi điểm $M'(x';y')$
thuộc d’ là ảnh của $M\left( x;y \right)$ thuộc d qua phép đối xứng tâm O nên $x'=-x$
và $y'=-y$
$\Rightarrow
(d'):-x-y+1=0$
Đáp án A
VD 2: Trong mặt phẳng Oxy cho đường tròn
tâm $I\left( 1;1 \right)$ bán kính R = 1. Tìm phương trình ảnh của đường tròn
qua phép đói xứng qua gốc tọa độ?
A.${{\left(
x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1$
B.${{\left(
x+1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=1$
C.${{\left(
x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=1$
D.${{\left(
x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1$
Giải:
Gọi I’ tâm của
đường tròn ảnh
$\Rightarrow
I'\left( -1;-1 \right)$
Phép đối xứng
tâm không làm thay đổi bán kính đường tròn, nên phương trình của đường tròn ảnh
là:
${{\left(
x+1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=1$
Đáp án B
VD 3: Trong mặt phẳng Oxy cho đường thẳng $\left(
d \right):x+y+1=0$ để phép đối xứng tâm I biến $\left( d \right)$ thành chính
nó thì I có thể là điểm nào sau đây?
A.$\left(
0;1 \right)$
B.$\left(
1;0 \right)$
C.$\left(
-1;-1 \right)$
D.$\left(
-1;0 \right)$
Giải:
Để phép đối
xứng tâm I biến một đường thẳng thành chính nó thì tâm I phải thuộc đường thẳng
đó
Nên từ 4 đáp
án, ta thấy chỉ đáp án D thõa mãn $I\in \left( d \right)$
Đáp án D
VD 4: Trong mặt phẳng Oxy cho 2 điểm $A\left(
1;2 \right)$ và $B\left( -3;6 \right)$ . Tìm tọa độ tâm đối xứng biết phép đối
xứng tâm I biến điểm A thành B.
A.$\left(
-2;2 \right)$
B.$\left(
-1;4 \right)$
C.$\left(
-2;8 \right)$
D.$\left(
-4;4 \right)$
Giải:
Theo biểu thức
tọa độ, ta có $I\left( {{x}_{I}};{{y}_{I}} \right)$ nên:
${{x}_{I}}=\frac{{{x}_{A}}+{{x}_{B}}}{2}=\frac{1-3}{2}=-1$
${{y}_{I}}=\frac{{{y}_{A}}+{{y}_{B}}}{2}=\frac{2+6}{2}=4$
$\Rightarrow
I\left( -1;4 \right)$
Đáp án B
VD 5: Cho đường thẳng $\left( d
\right):x+y+2=0$ và điểm $I\left( 1;1 \right)$ . Tìm ảnh của d qua phép đối xứng
tâm I
A.$x-y+2=0$
B.$-x+y-2=0$
C.$x-y-2=0$
D.$x+y+2=0$
Giải:
+ Chọn điểm $A\left(
-2;0 \right)\in \left( d \right)$
Gọi $A'\left(
{{x}_{A'}};{{y}_{A'}} \right)$ là ảnh của $A\left( -2;0 \right)$ qua phép đối xứng
tâm $I\left( 1;1 \right)$ , suy ra:
${{x}_{A'}}=2.1-\left(
-2 \right)=4$
${{y}_{A'}}=2.1-0=2$
$\Rightarrow
A'\left( 4;2 \right)$
+ Chọn điểm $A\left(
0;-2 \right)\in \left( d \right)$
Gọi $B'\left(
{{x}_{B'}};{{y}_{B'}} \right)$ là ảnh của $A\left( 0;-2 \right)$ qua phép đối xứng
tâm $I\left( 1;1 \right)$ , suy ra:
${{x}_{B'}}=2.1-0=2$
${{y}_{B'}}=2.1-\left(
-2 \right)=4$
$\Rightarrow
B'\left( 2;4 \right)$
$\Rightarrow
$ $\left( d' \right)$ đi qua $A'\left( 4;2 \right)$ và nhận $\overrightarrow{A'B'}\left(
-2;2 \right)$ làm VTCP
$\Rightarrow
\left( d' \right):-2\left( x-4 \right)+2\left( y-2 \right)=0$
$\Leftrightarrow
-2x+2y+4=0$
$\Leftrightarrow
x-y-2=0$
Đáp án C
C/ BÀI TẬP
Bài 1: Trong mặt phẳng Oxy, cho đường thẳng $\left(
d \right):3x-2y-1=0$ . Anhir của đường thẳng d qua phép đối xứng tâm O có
phương trình:
A.$3x+2y-1=0$
B.$-3x+2y-1=0$
C.$3x-2y-1=0$
D.$3x+2y+1=0$
Bài 2: Trong mặt phẳng Oxy, cho đường thẳng $\left(
d \right):Ax+By+C=0$ và $M\left( a;b \right)$. Phép đối xứng tâm biến đường thẳng
$\left( d \right)$ thành đường thẳng $\left( d' \right)$ . Phương trình đường
thẳng $\left( d' \right)$ là:
A.$Ax+By+C-2aA-2bB=0$
B.$Ax-By+C-2aA-2bB=0$
C.$Ax-By-C-2aA-2bB=0$
D.$Ax+By-C-2aA-2bB=0$
Bài 3: Hợp thành của một phép tịnh tiến và
phép đối xứng tâm là phép nào?
A.Phép đối xứng
trục
B.Phép tịnh
tiến
C.Phép đối xứng
tâm
D.Phép đồng
nhất
Bài 4: Trong mặt phẳng Oxy cho đường tròn tâm
$I\left( 3;2 \right)$ bán kính R = 1. Tìm phương trình ảnh của đường tròn qua
phép đói xứng qua gốc tọa độ?
A.${{\left(
x+3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=1$
B.${{\left(
x+3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=1$
C.${{\left(
x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=1$
D.${{\left(
x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=1$
Bài 5: Mệnh đề nào sau đây là đúng?
A.Tam giác đều
có tâm đối xứng
B.Tứ giác có
tâm đối xứng
C.Hình thang
cân có tâm đối xứng
D.Hình bình
hành có tâm đối xứng
Bài 6: Trong mặt phẳng Oxy, cho đường thẳng
x = 4. Tìm phương trình đường thẳng là ảnh của đường thẳng trên qua phép đối xứng
tâm O
A.$x=-4$
B.$y=4$
C.$y=-4$
D.$x=4$
Bài 7: Cho điểm $A\left( 2;3 \right)$ . Tìm
tọa độ điểm B biết phép đối xứng tâm O biến điểm B thành điểm A.
A.$\left(
-2;3 \right)$
B.$\left(
-2;-3 \right)$
C.$\left(
2;-3 \right)$
D.$\left(
3;2 \right)$
Bài 8: Cho điểm $A\left( 1;1 \right)$ và $B\left(
3;7 \right)$ . Tìm điểm C là ảnh của A qua phép đối xứng tâm B
A.$\left(
4;8 \right)$
B.$\left(
2;6 \right)$
C.$\left(
-5;13 \right)$
D.$\left(
5;13 \right)$
Bài 9: Trong mặt phẳng Oxy cho đường thẳng $\left(
d \right):2x+3y=0$ . Để phép đối xứng tâm I biến d thành chính nó thì I có thể
là điểm nào sau đây?
A.$\left(
-3;-2 \right)$
B.$\left(
3;2 \right)$
C.$\left(
-3;2 \right)$
D.$\left(
3;-2 \right)$
Bài 10: Cho điểm $A\left( 1;4 \right)$ và $B\left(
3;2 \right)$ . Tìm tọa độ tâm đối xứng I biết phép đối xứng tâm I biến điểm A
thành điểm B.
A.$\left(
4;6 \right)$
B.$\left(
1;1 \right)$
C.$\left(
2;3 \right)$
D.$\left(
3;2 \right)$
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
D |
C |
A |
D |
A |
B |
D |
A |
C |







