PHÉP QUAY
A/ LÝ THUYẾT
I/ Định nghĩa
+ Cho điểm I
và góc lượng giác $\alpha $ . Phép biến hình biến I thành chính nó, biến mỗi điểm
M khác I thành điểm M’ sao cho IM’ = IM và góc lượng giác $\left( IM'IM'
\right)=\alpha $ được gọi là phép quay tâm I góc $\alpha $
+ Kí hiệu: 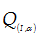
+ Các trường
hợp đặc biệt:
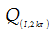 là phép đồng nhất (biến
mọi điểm thành chính nó)
là phép đồng nhất (biến
mọi điểm thành chính nó)
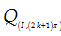 là
phép đối xứng tâm I
là
phép đối xứng tâm I
II/ Biểu thức tọa độ của
phép quay
Giả sử điểm $I\left(
a;b \right)$ và góc quay $\alpha $. Khi đó 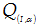 biến điểm $M\left( x;y \right)$
thành điểm $M'\left( x';y' \right)$ , với $x'$ và $y'$ tính theo công thức sau:
biến điểm $M\left( x;y \right)$
thành điểm $M'\left( x';y' \right)$ , với $x'$ và $y'$ tính theo công thức sau:
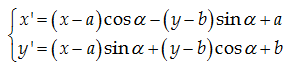
III/ Tính chất
+ Phép quay
bảo toàn khoảng cách giữa hai điểm
+ Phép quay
biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó,
biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng
bán kính
B/ VÍ DỤ
VD 1: Trong hệ tọa độ Oxy cho điểm $A\left(
3;3 \right)$ . Hỏi ảnh của điểm A qua phép quay tâm O góc quay ${{90}^{o}}$ là?
A.$\left(
3;-3 \right)$
B.$\left(
-3;3 \right)$
C.$\left(
3;3 \right)$
D.$\left(
-3;-3 \right)$
Giải:
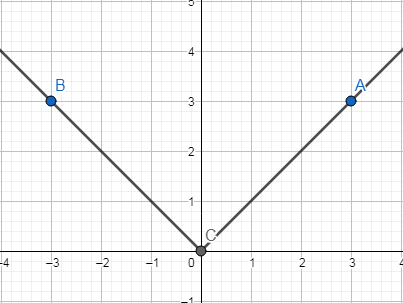
Gọi $B\left(
x;y \right)$ là ảnh của A qua phép quay tâm O góc quay ${{90}^{o}}$
Áp dụng công
thức, ta có:
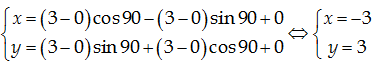
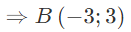
Đáp án B
VD 2: Trong hệ tọa độ Oxy cho điểm $A\left(
3;3 \right)$ . Hỏi ảnh của điểm A qua phép quay tâm O góc quay $-{{90}^{o}}$
là?
A.$\left( 3;-3 \right)$
B.$\left(
-3;3 \right)$
C.$\left(
3;3 \right)$
D.$\left(
-3;-3 \right)$
Giải:
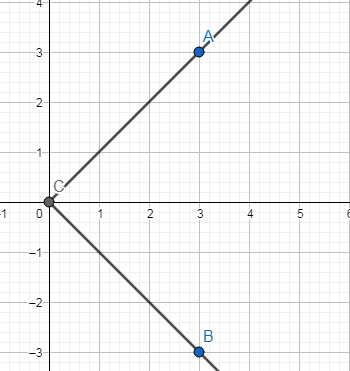
Gọi $B\left(
x;y \right)$ là ảnh của A qua phép quay tâm O góc quay $-{{90}^{o}}$
Áp dụng công
thức, ta có:
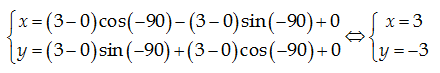
$\Rightarrow
B\left( 3;-3 \right)$
Đáp án A
VD 3: Cho hai điểm $A\left( 0;2 \right)$ và
$B\left( 2;0 \right)$ hỏi phép quay nào dưới đây biến điểm A thành điểm B?
A.${{Q}_{\left(
O;\frac{\pi }{2} \right)}}$
B.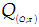
C.${{Q}_{\left(
O;\frac{3\pi }{2} \right)}}$
D.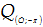
Giải:
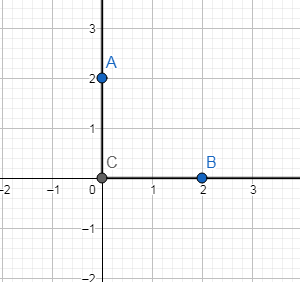
Nhìn vào
hình vẽ ta thấy chỉ có phép quay ${{Q}_{\left( O;\frac{3\pi }{2} \right)}}$ hoặc
${{Q}_{\left( O;-\frac{\pi }{2} \right)}}$biến điểm A thành điểm B
Đáp án C
VD 4: Trong mặt phẳng tọa độ Oxy cho đường
thẳng $\left( d \right):x-y=0$ . Tìm ảnh của đường thẳng (d) qua phép quay tâm
O góc quay ${{90}^{o}}$
A.$x+y+1=0$
B.$x+y-1=0$
C.$x+y=0$
D.$-x+y-2=0$
Giải:
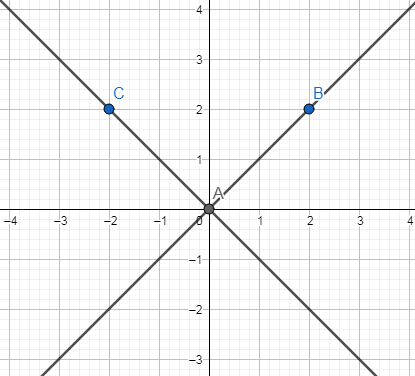
Gọi điểm $O\left(
0;0 \right)$ và điểm $B\left( 2;2 \right)$ thuộc (d)
Khi đó ảnh của
hai điểm O và B qua phép quay tâm O góc quay ${{90}^{o}}$ lần lượt là $\left(
0;0 \right)$ và:
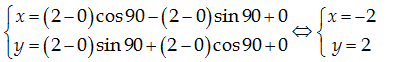
$\Rightarrow
C\left( -2;2 \right)$
Đường thẳng $\left(
d' \right)$ qua $O\left( 0;0 \right)$ nhận $\overrightarrow{OC}\left( -2;2
\right)$ và VTCP
$\Rightarrow
\left( d' \right):x+y=0$
Đáp án C
VD 5: Cho hình bình hành ABCD tâm O, phép
quay tâm O, góc quay $-{{180}^{o}}$ biến đường thẳng AD thành đường thẳng nào
trong số các đường thẳng dưới đây?
A.CD
B.BC
C.BA
D.AC
Giải:
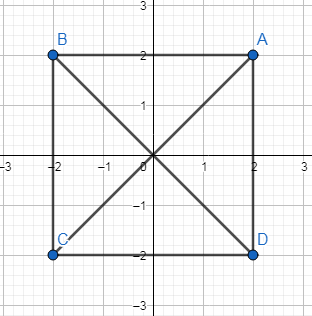
Phép quay
tâm O góc quay $-{{180}^{o}}$ biến điểm A thành điểm C
Phép quay
tâm O góc quay $-{{180}^{o}}$ biến điểm B thành điểm B
$\Rightarrow
$ Phép quay tâm O góc quay $-{{180}^{o}}$ biến đoạn thẳng AD thành đoạn thẳng
BC
Đáp án B
C/ BÀI TẬP
Bài 1: Trong hệ trục tọa độ Oxy cho điểm $A\left(
4;4 \right)$ . Hỏi ảnh của điểm A qua phép quya tâm O góc quay $-{{90}^{o}}$ là
điểm nào?
A.$\left(
4;4 \right)$
B.$\left(
4;-4 \right)$
C.$\left(
-4;4 \right)$
D.$\left(
-4;-4 \right)$
Bài 2: Cho hai điểm $A\left( 0;4 \right)$ và
$B\left( 4;0 \right)$ . Hỏi phép quay nào dưới đây biến điểm A thành điểm B?
A.${{Q}_{\left(
O;\frac{\pi }{2} \right)}}$
B.${{Q}_{\left(
O;\frac{3\pi }{2} \right)}}$
C.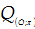
D.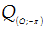
Bài 3: Cho hình vuông tâm ABCD có O là giao
điểm hai đường chéo. Xác định ảnh của đường thẳng BC quay phép quay tâm O góc
quay ${{90}^{o}}$
A.Đường thẳng
CD
B.Đường thẳng
DA
C.Đường thẳng
AB
D.Đường thẳng
CA
Bài 4: Trong
mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình $x+y-2=0$ . Tìm ảnh của
đường thẳng d qua phép quay tâm O góc quay ${{90}^{o}}$ ?
A.$-x-y-2=0$
B.$x-y-2=0$
C.$x+y+2=0$
D.$x-y+2=0$
Bài 5: Cho hình chữ nhật có O là tâm đối xứng.
Hỏi có bao nhiêu phép quay tâm O, góc 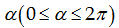 biến hình chữ nhật trên thành chính
nó?
biến hình chữ nhật trên thành chính
nó?
A.0
B.1
C.2
D.Vô số
Bài 6: Cho hình vuông ABCD tâm O. Xét phép
quay tâm O góc quay $\varphi $ . Với giá trị nào sau đây của $\varphi $, phép
quay $Q$ biến hình vuông ABCD thành chính nó?
A.$\varphi
=\frac{\pi }{6}$
B.$\varphi
=\frac{\pi }{4}$
C.$\varphi
=\frac{\pi }{3}$
D.$\varphi
=\frac{\pi }{2}$
Bài 7: Trong mặt phẳng tọa độ Oxy, cho đường
thẳng $\left( d \right):x+y-2=0$ . Tìm ảnh của d qua phép quay tâm O, góc quay ${{90}^{o}}$
A.$x+y+2=0$
B.$x-y+2=0$
C.$x+y-2=0$
D.$x-y-2=0$
Bài 8: Cho hai đường thẳng bất kì d và d’.
Có bao nhiêu phép quay biến đường thẳng d thành đường thẳng d’?
A.0
B.1
C.2
D.Vô số
Bài 9: Trong các chữ cái và chữ số sau, dãy
các chữ cái, chữ số nào mà khi ta thực hiện phép quay tâm A một góc ${{180}^{o}}$
thì ta được một phép đồng nhất?
A.$O,I,0,8,S$
B.$X,L,6,1,U$
C.$O,Z,V,9,5$
D.$H,J,K,4,8$
Bài 10: Cho tam giác ABC, ${{Q}_{\left(
O{{,30}^{o}} \right)}}\left( A \right)=A'$ , ${{Q}_{\left( O{{,30}^{o}} \right)}}\left(
B \right)=B'$ , ${{Q}_{\left( O{{,30}^{o}} \right)}}\left( C \right)=C'$ . Với
O khác A, B, C. Kết luận nào sau đây là đúng?
A.$\vartriangle
ABC$ đều
B.$\vartriangle
ABC$ cân
C.$\vartriangle
AOA'$ đều
D.$\vartriangle
AOA'$ cân
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
B |
C |
D |
C |
D |
B |
D |
A |
C |







