PHÉP ĐỐI XỨNG TRỤC
A/ LÝ THUYẾT
I/ Định nghĩa
Cho đường thẳng
d. Phép biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d
thành điểm M’ sao cho d là đường trung trực của MM’, được gọi là phép đối xứng
qua đường thẳng d (hay là phép đối xứng trục. Đường thẳng d gọi là trục đối xứng.
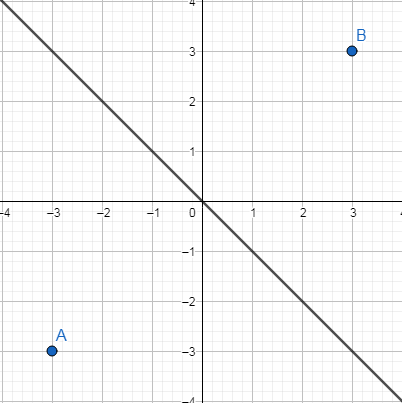
Ví dụ:
$B\left( 3;3 \right)$ là ảnh của $A\left( -3;-3 \right)$ ; $O\left( 0;0 \right)$ là ảnh của $O\left( 0;0 \right)$ qua phép đối xứng trục có trục đối xứng là đường thẳng $y=-x$
II/ Biểu thức tọa độ của
phép đối xứng trục
Ta chọn đường
thẳng d trùng với trục Ox. Với mỗi điểm $M\left( x;y \right)$ , gọi $M'\left(
x';y' \right)$ là ảnh của M qua phép đối xứng trục thì thì $x=x'$ và $y=-y'$
III/ Tính chất
a/ Tính chất 1
Phép đối xứng
trục bảo toàn khoảng cách giữa hai điểm bất kì
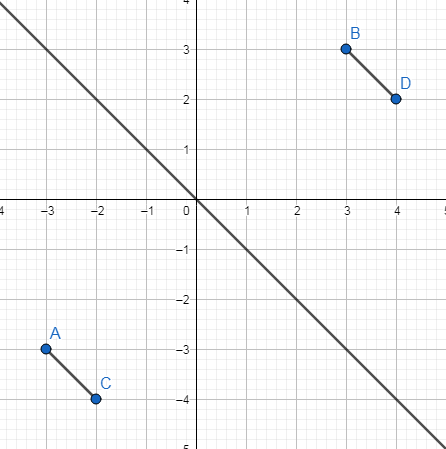
Ví dụ:
Phép đối xứng
trục nhận trục đối xứng là đường thẳng $y=-x$
Biến điểm $A\left(
-3;-3 \right)$ thành điểm $B\left( 3;3 \right)$
Biến điểm $C\left(
-2;-4 \right)$ thành điểm $D\left( 4;2 \right)$
Ta có:
$AC=\sqrt{{{\left(
-3+2 \right)}^{2}}+{{\left( -3+4 \right)}^{2}}}=\sqrt{2}$
$BD=\sqrt{{{\left(
3-4 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}}=\sqrt{2}$
Ta thấy $AC=BD$
$\Rightarrow $ Phép đối xứng trục bảo toàn khoảng cách
b/ Tính chất 2
Phép đối xứng
trục biến một đường thẳng thành một đường thẳng, biến một đoạn thẳng thành một
đoạn thẳng bằng nó, biến một tam giác thành một tam giác bằng nó, biến một đường
tròn thành một đường tròn có cùng bán kính
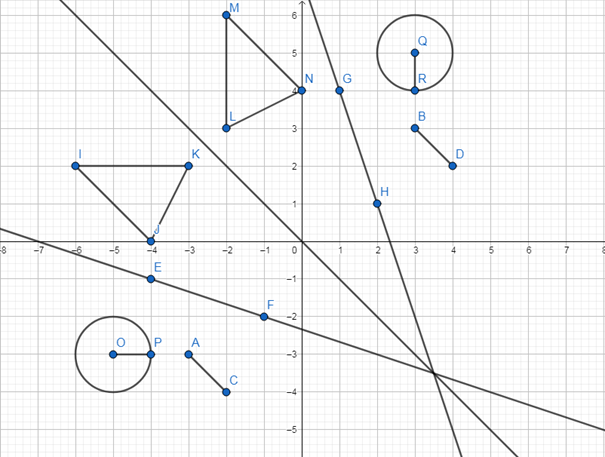
Ví dụ:
Phép đối xứng trục nhận trục đối xứng là đường thẳng $y=-x$ (như hình vẽ)
IV/ Trục đối xứng của một
hình
1/ Định nghĩa
Đường thẳng
d được gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến hình H thành
chính nó
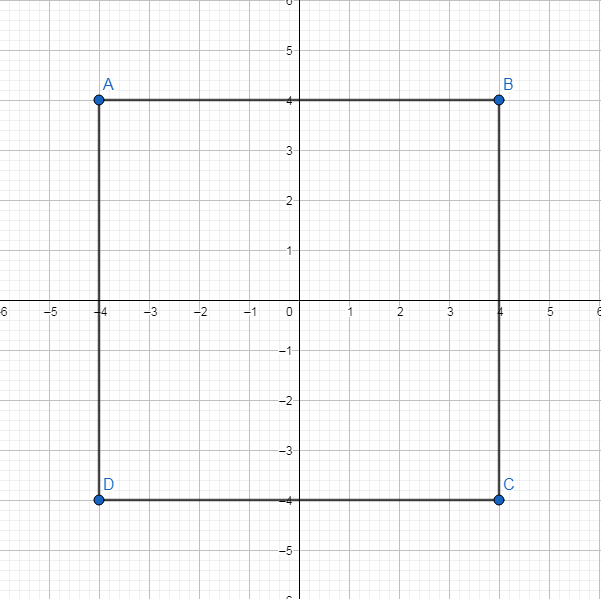
Ví dụ:
Hình vuông dưới đây nhận Ox là trục đối xứng
2/ Ví dụ
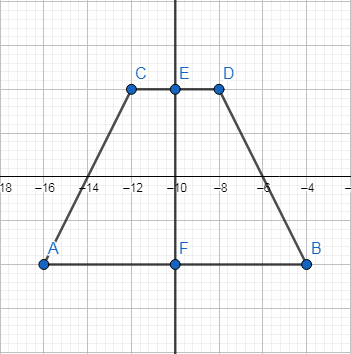
Hình thang cân có trục đối xứng là đường thẳng nối trung điểm của hai cạnh đáy
B/ BÀI TẬP
Câu 1: Tam giác đều có bao nhiêu trục đối xứng?
A.3
B.2
C.1
D.6
Câu 2: Hình vuông có bao nhiêu trục đối xứng?
A.2
B.4
C.3
D.6
Câu 3: Hình chữ nhật (không phải là hình
vuông) có bao nhiêu trục đối xứng?
A.4
B.3
C.2
D.1
Câu 4: Hình thang cân có bao nhiêu trục đối
xứng?
A.4
B.3
C.2
D.1
Câu 5: Trong mặt phẳng Oxy cho đường thẳng d
có phương trình $3x-y+2=0$ . Viết phương trình đường thẳng d’ là ảnh của d qua
phép đối xứng trục Oy?
A.$-3x-y+2=0$
B.$-3x+y+2=0$
C.$-3x-y-2=0$
D.$-x-3y+2=0$
Câu 6: Trong mặt phẳng Oxy, cho điểm $M(2;3)$
. Hỏi M là ảnh của điểm nào trong các điểm sau đây khi qua phép đối xứng trục
Oy?
A.$\left(
3;2 \right)$
B.$\left(
-2;3 \right)$
C.$\left(
3;-2 \right)$
D.$\left(
2;-3 \right)$
Câu 7: Mệnh đề nào sau đây là đúng?
A.Một hình
có vô số trục đối xứng thì đó phải là đường tròn
B.Một hình
có vô số trục đối xứng thì đó phải là hình gồm hai đường thẳng vuông góc
C.Đường tròn
là hình có vô số trục đối xứng
D.Một hình
có vô số trục đối xứng thì đó phải là hình gồm những đường tròn đồng tâm
Câu 8: Cho hai đường thẳng cắt nhau d và d’.
Có bao nhiêu phép đối xứng trục biến đường thẳng d thành d’?
A.0
B.1
C.3
D.2
Câu 9: Trong các hình sau, hình nào có 4 trục
đối xứng?
A.Hình vuông
B.Hình bình
hành
C.Hình thoi
D.Hình chữ
nhật
Câu 10: Trong mặt phẳng Oxy, đường thẳng d có
phương trình $3x-2y+1=0$ . Ảnh của đường thẳng d qua phép đối xứng trục Ox có
phương trình là:
A.$3x+2y-1=0$
B.$3x+2y+1=0$
C.$-3x+2y+1=0$
D.$3x-2y+1=0$
Câu 11: Viết phương trình ảnh của đường tròn $\left(
C \right):{{x}^{2}}+{{y}^{2}}-4x+5y+1=0$ qua phép đối xứng trục Oy:
A. ${{x}^{2}}+{{y}^{2}}-4x+5y+1=0$
B. ${{x}^{2}}+{{y}^{2}}-4x-5y+1=0$
C. ${{x}^{2}}+{{y}^{2}}+4x+5y+1=0$
D.${{x}^{2}}+{{y}^{2}}+4x-5y+1=0$
Câu 12: Cho lục giác đều ABCDEF tâm O. Tìm ảnh
của tam giác AOF qua phép đối xứng qua
đường thẳng BE
A.$\vartriangle
AOB$
B. \[\vartriangle
BOC\]
C.\[\vartriangle
EOF\]
D. $\vartriangle
COD$
Câu 13: Hợp thành của hai phép đối xứng trục
có trục vuông góc với nhau là phép nào trong các phép sau đây?
A.Phép đối xứng
tâm
B.Phép tịnh
tiến
C.Phép đối xứng
trục
D.Phép đồng
nhất
Câu 14: Trong hệ trục tọa độ Oxy, cho điểm $M(2;3)$
. Trong các khẳng định sau, khẳng định nào là đúng?
A. Phép đối
xứng trục Oy biến $M$ thành $M'\left( 2;-3 \right)$
B.Phép đối xứng
trục Ox biến $M$ thành $M'\left( 2;-3 \right)$
C. Phép đối
xứng trục Oy biến $M$ thành $M'\left( 3;2 \right)$
D. Phép đối
xứng trục Ox biến $M$ thành $M'\left( 3;2 \right)$
Câu 15: Trong mặt phẳng Oxy, đường thẳng d có
phương trình $x-2y+3=0$ . Ảnh của đường thẳng d qua phép đối xứng trục Ox có
phương trình là:
A.$x+2y-3=0$
B.$x-2y+3=0$
C.$x+2y+3=0$
D.$-x+2y+3=0$
Câu 16: Cho điểm $M\left( 1;2 \right)$ và đường thẳng d có phương
trình $x+y-2=0$ . Tìm tọa độ ảnh của M qua phép đối xứng trục d
A.$\left(
-1;0 \right)$
B.$\left(
0;-1 \right)$
C.$\left(
1;0 \right)$
D.$\left(
0;1 \right)$
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
A |
B |
C |
D |
A |
B |
C |
D |
A |
B |
C |
D |
A |
B |
C |
D |







