QUANG HỆ ĐỒNG TRỤC(P1)
1. Giải bài tập quang hệ cho từng thấu kính.
1.1 Phương pháp giải.
Giải bài toán hệ quang học nói chung (hệ thấu kính nói riêng) bao gồm hai bước:
- Bước 1: Lập sơ đồ tạo ảnh.
- Bước 2: Áp dụng các công thức liên quan cho mỗi khâu của sơ đồ để giải bài toán theo yêu cầu của đề (quy ước dấu đối với vật ở trước thấu kính thì d > 0 và ở sau thấu kính thì d < 0, d là khoảng cách từ vật tới thấu kính. Đối với khoảng cách \[\text{d }\!\!'\!\!\text{ }\] từ ảnh tới thấu kính thì quy ước ngược lại so với vật).
+ Công thức thấu kính:\[\frac{1}{d}+\frac{1}{{{d}^{'}}}=\frac{1}{f}\]
+ Xác định số phóng đại ảnh: \[k=\frac{{{d}^{'}}}{d}{{k}_{he}}={{k}_{1}}.{{k}_{2}}=\frac{d_{1}^{'}}{{{d}_{1}}}.\frac{d_{2}^{'}}{{{d}_{2}}}\]
+ Độ tụ của hệ 2 thấu kính mỏng đồng trục ghép sát:
D = D1 + D2 hay \[\frac{1}{f}=\frac{1}{{{f}_{1}}}+\frac{1}{{{f}_{2}}}\]. Đặc điểm ảnh của vật AB tạo bởi hệ 2 thấu kính ghép là đặc điểm ảnh của vật AB tạo bởi thấu kính tương đương.
+ Nguyên lý thuận nghịch của sự truyền ánh sáng: Nếu ánh sáng truyền đi theo đường nào thì cũng truyền ngược lại theo đường đó (nếu ánh sáng từ môi trường (1) sang môi trường (2) theo đường \[\text{AI{A}'}\] thì cũng truyền theo chiều \[\text{{A}'IA}\] từ môi trường (2) sang môi trường (1).
a. Hệ 2 thấu kính đồng trục ghép cách nhau một đoạn l:
Giả sử vật thật AB đặt trên trục chính của hệ 2 thấu kính đồng trục L1 và L2 . Giả sử AB có ảnh A1B1tạo bởi L1, ảnh A1B1 này coi là vật đối với L2.
Nếu A1B1 ở trước L2 thì đó là vật thật.
Nếu A1B1 ở sau L2 thì đó là vật ảo.
Thấu kính L2 cho ảnh A2B2 của vật A1B1 . Vậy A2B2 là ảnh cuối cùng qua hệ.
Vậy A2B2 là ảnh sau cùng của AB qua hệ thấu kính.
b. Hệ 2 thấu kính đồng trục ghép sát nhau:
Với hệ này có 2 cách:
+ Lập sơ đồ như hệ 2 thấu kính đồng trục ghép cách nhưng khoảng cách L1 đến L2 là l = 0.
+ Hoặc dùng thấu kính tương đương là tiện lợi:
.png)
Giả sử vật thật AB trên trục chính của hệ 2 thấu kính đồng trục L1 và L2 ghép sát tương tự mục (a) ta có sơ đồ tạo ảnh
.png)
Khi áp dụng công thức về thấu kính để giải chỉ cần nhớ l là khoảng cách 2 thấu kính luôn bằng 0: \[d_{1}^{'}+{{d}_{2}}=0\Rightarrow {{d}_{2}}=-d_{1}^{'}\]
Ta có: \[\frac{1}{{{d}_{1}}}+\frac{1}{d_{1}^{'}}=\frac{1}{{{f}_{1}}}\] và: \[\frac{1}{{{d}_{2}}}+\frac{1}{d_{2}^{'}}=\frac{1}{{{f}_{2}}}\]
Mà ta luôn có d2 = -d1 Suy ra:
.png) \
\
+ Nhận thấy 2 thấu kính f1, f2 ghép sát tương ứng với hệ thấu kính có tiêu cự f: \[\frac{1}{{{f}_{1}}}+\frac{1}{{{f}_{2}}}=\frac{1}{f}\] hay D1 + D2 = D.
Lúc này ta có sơ đồ tạo ảnh:
.png)
Thực hiện tính toán.
Nội dung khảo sát của 1 hệ thấu kính rất đa dạng, nhưng nhìn chung thường gặp 3 yêu cầu chính:
(1). Xác định các đặc điểm của ảnh sau cùng.
(2). Xác định các đặc điểm cấu tạo của hệ.
(3). Tìm điều kiện để hệ cho ảnh ảo, ảnh thật, 2 ảnh, 1 ảnh duy nhất.
Để giải đáp được 3 yêu cầu này, cần lưu ý đến 3 kết quả sau:
+ Ảnh A1B1 qua L1 được xác định bởi \[{{\text{d}}_{1}}^{\prime }\].
Khi A1B1 đóng vai trò vật với L2 thì đặc điểm của nó được xác định bởi d2, trong mọi trường hợp, ta luôn có \[{{\text{d}}_{1}}^{\prime }\] + d2 = l; hay d2 = l – \[{{\text{d}}_{1}}^{\prime }\] (l là khoảng cách giữa 2 thấu kính).
+ Số phóng đại ảnh sau cùng được xác định bởi:
\[k=\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{AB}}=\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{{{A}_{1}}{{B}_{1}}}}.\frac{\overline{{{A}_{1}}{{B}_{1}}}}{\overline{AB}}={{k}_{1}}{{k}_{2}}=\frac{d_{1}^{'}d_{2}^{'}}{{{d}_{1}}{{d}_{2}}}\]
+ Hệ vô tiêu: ảnh cuối cùng \[{{\text{A}}_{2}}^{\prime }{{\text{B}}_{2}}^{\prime }\] có độ lớn không đổi khi ta di chuyển vật lại gần thấu kính: l = f1 + f2 (chú ý: f1, f2 có giá trị đại số: dương với thấu kính hội tụ, âm với thấu kính phân kỳ).
Bài 1: Trước thấu kính hội tụ (L1) (tiêu cự f1 = 10cm), có vật sáng AB đặt vuông góc với trục chính, cách thấu kính đoạn d1 = 40cm.
a. Xác định ảnh A1B1 của AB tạo bởi (L1) . Vẽ đường đi của chùm tia sáng từ B.
b. Sau (L1) và cách (L1) đoạn a = 4cm, đặt thêm thấu kính phân kì (L2) có tụ số D2 = - 10dp sao cho hai trục chính trùng nhau.Xác định ảnh $\text{{A}'{B}'}$ của vật tạo bởi hệ hai thấu kính.
c. Bây giờ AB ở rất xa hệ hai thấu kính. Người ta muốn thay hệ hai thấu kính (L1, L2) bằng một thấu kính hội tụ (L) sao cho ảnh của AB tạo bởi hệ (L1, L2) và bởi (L) có vị trí trùng nhau, độ lớn bằng nhau.Tính tiêu cự của (L) và định vị trí của (L) đối với (L2).
Bài giải:
a. Xác định ảnh A1B1 Ta có: d1 = 400cm >> f1 cm.
.png)
Có thể coi là vật AB ở vô cực so với (L1). Ảnh A1B1được tạo ra tại tiêu diện ảnh.
${{\text{d}}_{1}}^{\prime }=10\text{cm}$.
Do đó:${{\text{k}}_{1}}=-\frac{{{\text{d}}_{1}}^{\prime }}{{{\text{d}}_{1}}}=-\frac{1}{40}=-0,025$
Ảnh thật ngược chiều bằng 1/40 vật và cách thấu kính 10 cm.
Đường đi của chùm tia sáng từ B:
b. Xác định ảnh $\text{{A}'{B}'}$:
.png)
Sơ đồ tạo ảnh:
.png)
Theo trên ta có:
\[{{\text{d}}_{1}}^{\prime }=10\text{cm}\text{.}\]\[{{\text{d}}_{1}}^{\prime }=10\text{cm}\text{.}\]
Do đó:
.png)
Ảnh $\text{{A}'{B}'}$ là ảnh thật, cách thấu kính (L2) một đoạn 15cm.
Ta cũng có:
.png)
Ảnh ngược chiều với vật và bằng $\frac{1}{16}$ lần vật.
c. Tiêu cự và vị trí của thấu kính tương đương.
AB $\text{{{A}'}'{{B}'}'}$
Vì $\overline{\text{{{A}'}'{{B}'}'}}=\overline{\text{{A}'{B}'}}$ nên $\text{{{A}'}'{{B}'}'}$ cũng ngược chiều với vật. (L) phải là thấu kính hội tụ.
Vì AB ở rất xa ta có:
$\text{{{A}'}'{{B}'}'}=\text{f}\text{. tan }\!\!\alpha\!\!\text{ }\approx \text{f}\text{. }\!\!\alpha\!\!\text{ }$($\text{ }\!\!\alpha\!\!\text{ }$ góc trông của AB)
Đối với hệ (L1 + L2):
$\frac{\text{{A}'{B}'}}{{{\text{A}}_{1}}{{\text{B}}_{1}}}=\left| {{\text{k}}_{2}} \right|=\left| \frac{{{{\text{{d}'}}}_{2}}}{{{\text{d}}_{2}}} \right|;\text{ }{{\text{A}}_{1}}{{\text{B}}_{1}}={{\text{f}}_{1}}\text{. tan }\!\!\alpha\!\!\text{ }\approx {{\text{f}}_{1}}\text{. }\!\!\alpha\!\!\text{ }$$\Rightarrow \text{{A}'{B}'}=\left| \frac{{{{\text{{d}'}}}_{2}}}{{{\text{d}}_{2}}} \right|.{{\text{f}}_{1}}\text{. }\!\!\alpha\!\!\text{ }.
Theo đề ta suy ra:
\[\text{f}=\left| \frac{{{{\text{{d}'}}}_{2}}}{{{\text{d}}_{2}}} \right|.{{\text{f}}_{1}}=\frac{15}{6}.10=25\left( \text{cm} \right)\]
Vị trí của (L) được xác định bởi:
${{\text{O}}_{\text{2}}}\text{O}=\text{f}-{{\text{d}}_{\text{2}}}^{\prime }=25-15=10\text{cm}\text{.}$
Bài 2: Cho hệ đồng trục hai thấu kính hội tụ L1, L2 lần lượt có tiêu cự f1 = 30cm, f2 = 20cm, đặt cách nhau 15cm. Nguồn điểm S ở trên trục trước L1 và cách L1 10 cm.
a. Xác định ảnh $\text{{S}'}$ tạo bởi hệ.
b. Giữ vật S và L1 cố định, tịnh tiến L2 xa dần L1. Hỏi ảnh dịch chuyển như thế nào?
c. Giữ cố định khoảng cách giữa S và L1, L2, tịnh tiến L1 theo hướng vuông góc với trục một đoạn 2cm. Xác định vị trí của ảnh cho bởi hai thấu kính.
Bài giải:
a. Ta có sơ đồ tạo ảnh S qua hệ qua hệ L1, L2:
.png)
S cho qua L1 ảnh ảo S1 xác định bởi:
\[\overline{\text{O}{{\text{S}}_{1}}}={{\text{d}}_{1}}^{\prime }=\frac{{{\text{d}}_{1}}{{\text{f}}_{1}}}{{{\text{d}}_{1}}-{{\text{f}}_{1}}}=\frac{15.30}{15-30}=-15\text{cm}<0\Leftrightarrow {{\text{S}}_{1}}:\] ảo.
$\text{d}=1-{{\text{d}}_{1}}^{\prime }=15-\left( -15 \right)=30\text{cm}>0.$
$\Leftrightarrow {{\text{S}}_{\text{1}}}$ là vật thật của L2 cho qua L2 ảnh $\text{{S}'}$ xác định bởi:
${{\text{d}}_{2}}^{\prime }={{\text{O}}_{\text{2}}}\text{{B}'}=\frac{{{\text{d}}_{2}}{{\text{f}}_{2}}}{{{\text{d}}_{2}}-{{\text{f}}_{2}}}=\frac{30.20}{30-20}=60\text{cm}>0$
$\Leftrightarrow \text{{S}'}$ là ảnh thật cách L2 60cm.
b. Giữ S và L1 cố định nên S1 cố định. Ở vị trí ban đầu điểm vật thật S1 cách thấu kính L2một đoạn d2 = 30cm.
.png)
(Bài toán trở thành: cho điểm vật thật S1 cố định cách thấu kính hội tụ L2 một đoạn xs = do = 30 cm và S1 ở trên trục chính kéo L2 ra xa vật theo hướng song song trục chính. Khảo sát chiều chuyển động của ảnh $\text{{S}'}$).
Khi tịnh tiến L2 ra xa S1 luôn luôn là vật thật ở ngoài O2F2 nên $\text{{F}'}$ luôn luôn là ảnh thật $\Leftrightarrow \text{{d}'}>0$.
Chọn S1 làm gốc tọa độ, chiều dương từ trái qua phải (chiều của tia sáng tới). Ta có:
${{\text{S}}_{\text{1}}}{{\text{O}}_{\text{1}}}=\text{d}=\text{x}$ với \[30\le \text{x}<\infty \].
Đặt: y = S1S = \[\text{d}+\text{{d}'}>\text{0}\]
\[\text{{d}'}=\frac{\text{d}{{\text{f}}_{2}}}{\text{d}-{{\text{f}}_{2}}}=\frac{20\text{x}}{\text{x}-20}\]\[{{\text{S}}_{\text{1}}}\text{{S}'}=\text{f}\left( \text{x} \right)=\text{y}=\text{d}+\text{{d}'}=\text{x}+\frac{20\text{x}}{\text{x}-20}=\frac{{{\text{x}}^{2}}}{\text{x}-20}.\]
Khi tịnh tiến L2 thì x tăng trong [30, ∞] và [30, ∞] $\in $ miền xác định của y.
Ta có: \[\text{{y}'}=\text{f}\left( \text{x} \right)=\frac{{{\text{x}}^{2}}-40\text{x}}{{{\left( \text{x}-20 \right)}^{2}}}\]; vì \[{{\left( \text{x}-20 \right)}^{2}}>0,\]
$\Rightarrow \text{{y}'}$ theo dấu của \[{{\text{x}}^{2}}-40\text{x}\].
Ta có bảng biến thiên theo thực tế quang học:
|
x |
30 |
|
40 |
|
60 |
∞ |
|
$\text{{y}'}$ |
|
$-$ |
0 |
+ |
|
|
|
$\text{y}=\text{f}\left( \text{x} \right)$ |
90 |
|
80 |
|
90 |
|
Xem bảng biến thiên trên ta thấy: Khi tịnh tiến L2 ra xa khoảng cách x = d tăng từ 30 đến 40 thì y = ${{\text{S}}_{\text{1}}}\text{{S}'}$ giảm từ 90cm đến 80cm nghĩa là $\text{{S}'}$ chuyển động ngược chiều ánh sáng tới và $\text{{S}'}$ dừng lại tại vị trí cực tiểu cách S1 một đoạn ${{\text{S}}_{\text{1}}}{{\text{{S}'}}_{\text{min}}}$= 80cm. Sau đó ${{\text{S}}_{\text{1}}}\text{{S}'}$ tăng dần tức là $\text{{S}'}$ lại chuyển động theo chiều ánh sáng tới.
c. Khoảng cách từ S tới L1, L2 không thay đổi nên khoảng cách \[{{\text{{d}'}}_{1}}=-15\text{cm}\] và d2 = 30cm, \[{{\text{{d}'}}_{2}}=60\text{cm}\text{.}\] Nhưng khi dịch chuyển L1 xuống một đoạn 2 cm thì S cách trục chính của L1 đoạn SK = OO1 = 2cm.
Dựng đường thẳng \[\left( \text{ }\!\!\delta\!\!\text{ } \right)\text{ // }{{\text{L}}_{2}}\] cách L2 đoạn 60cm, cắt trục chính của L2 tại $\text{{H}'}$. Ta có:
$\text{{S}'=}\left( \text{ }\!\!\delta\!\!\text{ } \right)\cap {{\text{S}}_{1}}{{\text{O}}_{2}}.$
Theo hình vẽ ta có:
\[\frac{\text{S{H}'}}{{{\text{S}}_{\text{1}}}\text{H}}=\frac{{{\text{O}}_{\text{2}}}\text{{H}'}}{{{\text{O}}_{\text{2}}}\text{H}}=\frac{60}{30}=2\] (a)
\[\frac{{{\text{S}}_{\text{1}}}\text{H}}{{{\text{O}}_{\text{2}}}{{{\text{{O}'}}}_{1}}}=\frac{\text{SH}}{\text{S}{{\text{O}}_{\text{1}}}}=\frac{15-10}{10}=\frac{5}{10}=0,5\] (b)
Từ (a) và (b) $\Rightarrow \frac{\text{{S}'{H}'}}{{{\text{S}}_{\text{1}}}\text{H}}.\frac{{{\text{S}}_{\text{1}}}\text{H}}{{{\text{O}}_{\text{1}}}\text{{H}'}}=1.$
$\frac{\text{{S}'{H}'}}{{{\text{O}}_{\text{1}}}\text{{O}'}}=1\Rightarrow \text{{S}'{H}'}=2\text{cm}\text{.}$
Vậy $\text{{S}'}$ ở phía dưới trục chính của L2 , cách L2 60cm và cách trục chính của L2 2cm.
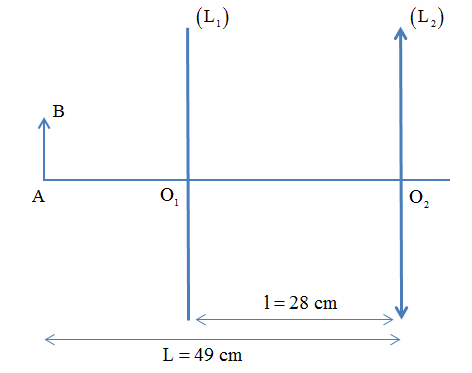
Bài 3: Một vật phẳng nhỏ AB đặt trên trục chính của một thấu kính hội tụ (O2) có tiêu cự f2 = 15cm và cách thấu kính 49cm. Đặt xen vào giữa vật và thấu kính (O2) một thấu kính (O1). Khi khoảng cách giữa hai thấu kính là 28cm, người ta thu được ảnh cuối cùng gấp 3 lần vật.
a. Định tiêu cự f1 của thấu kính (O1).
b. Vẽ đường đi của chùm tia sáng từ một điểm vật qua hệ hai thấu kính.
Bài giải:
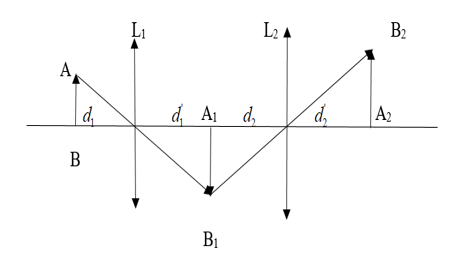
a. Sơ đồ tạo ảnh:
.png)
|
|
|
|
Xét lần lượt mỗi ảnh, ta có:
Với A1B1: d1 = 49 – 28 = 21 (cm)
${{\text{{d}'}}_{1}}=\frac{21{{\text{f}}_{1}}}{21-{{\text{f}}_{1}}}$
${{k}_{1}}=\frac{{{\text{f}}_{1}}}{{{\text{f}}_{1}}-{{\text{d}}_{1}}}=\frac{{{\text{f}}_{1}}}{{{\text{f}}_{1}}-\text{21}}$.
Với $\text{{A}'{B}'}$: d2 = l - ${{\text{{d}'}}_{1}}$ = 28 - $\frac{21{{\text{f}}_{1}}}{21-{{\text{f}}_{1}}}$= $\frac{588-49{{\text{f}}_{1}}}{21-{{\text{f}}_{1}}}$
k2 = $\frac{{{\text{f}}_{2}}}{{{\text{f}}_{2}}-{{\text{d}}_{2}}}=\frac{15}{15-\frac{588-49{{\text{f}}_{1}}}{21-{{\text{f}}_{1}}}}=\frac{15\left( 21-{{\text{f}}_{1}} \right)}{34{{\text{f}}_{1}}-273}$.
Theo đề:
\[\text{k}=\frac{\text{{A}'{B}'}}{\text{AB}}=\frac{\text{{A}'{B}'}}{{{\text{A}}_{1}}{{\text{B}}_{1}}}.\frac{{{\text{A}}_{1}}{{\text{B}}_{1}}}{\text{AB}}=\left| {{\text{k}}_{\text{2}}} \right|.{{\left| \text{k} \right|}_{\text{1}}}=3.\]
Suy ra:
$\frac{15\left| {{\text{f}}_{1}} \right|}{\left| 34{{\text{f}}_{1}}-273 \right|}=3\Rightarrow 5\left| {{\text{f}}_{1}} \right|=\left| 34{{\text{f}}_{1}}-273 \right|.$
Ta có hai trường hợp:
.png)
Vậy O1 là thấu kính hội tụ có tiêu cự 7cm hoặc 9,4cm.
b. Đường đi của chùm tia sáng:
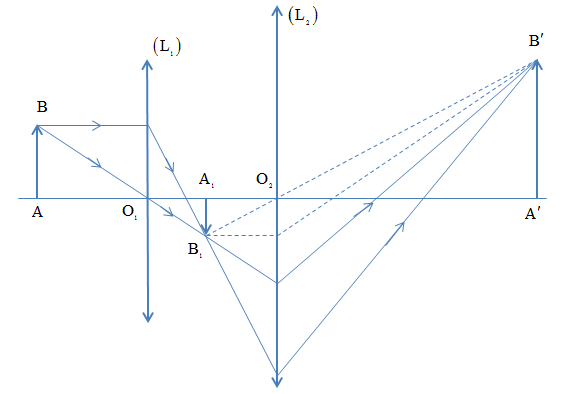
Bài 4: Cho hệ đồng trục gồm thấu kính hội tụ L1 tiêu cự f1 = 20cm và thấu kính phân kì L2 tiêu cự f2 = -40cm, đặt cách nhau 30cm, vật sáng AB = 20cm đặt vuông góc với trục và trước L1 một đoạn d1 = \[{{\text{O}}_{\text{1}}}\text{B}\]. Xác định d1 tức là xác định vị trí AB để:
a. Hệ cho ảnh thật.
b. Hệ cho ảnh ảo.
c. Hệ cho ảnh ảo 8 cm.
Bài giải:
Ta có sồ tạo ảnh
.png)
Ảnh A1B1 cách L1 một đoạn:
${{\text{{d}'}}_{1}}=\frac{{{\text{d}}_{1}}{{\text{f}}_{1}}}{{{\text{d}}_{1}}-{{\text{f}}_{1}}}=\frac{20{{\text{d}}_{1}}}{{{\text{d}}_{1}}-20}$
A1B1 trở thành vật của L2 cách L2 một hoành độ:
\[{{\text{d}}_{\text{2}}}=\text{l}~\text{ }{{\text{{d}'}}_{1}}=30-\frac{20{{\text{d}}_{1}}}{{{\text{d}}_{1}}-20}=\frac{10{{\text{d}}_{1}}-600}{{{\text{d}}_{1}}-20}.\]
${{\text{{d}'}}_{2}}=\overline{{{\text{O}}_{2}}\text{{A}'}}=\frac{{{\text{d}}_{2}}{{\text{f}}_{2}}}{{{\text{d}}_{2}}-{{\text{f}}_{2}}}=\frac{\left( 10{{\text{d}}_{1}}-600 \right)\left( -40 \right)}{\left( {{\text{d}}_{1}}-20 \right)\left( \frac{10{{\text{d}}_{1}}-600}{{{\text{d}}_{1}}-20}+40 \right)}$
${{\text{{d}'}}_{2}}=\frac{8\left( 60-{{\text{d}}_{1}} \right)}{{{\text{d}}_{1}}-28}$.
Xét dấu của ${{\text{{d}'}}_{2}}$ theo d1, ta có bảng xét dấu sau:
|
d1 |
0 |
|
28 |
|
60 |
|
$+\infty $ |
|
60 - d1 |
|
+ |
|
+ |
0 |
- |
|
|
d1 - 28 |
|
- |
0 |
+ |
|
+ |
|
|
${{\text{{d}'}}_{2}}$ |
|
|
- |
|
+ |
0 |
- |
Theo bảng xét dấu, ta có:
a. Hệ cho ảnh thật $\Leftrightarrow {{\text{{d}'}}_{2}}>0$ khi 28 < d1< 60.
b. Hệ cho ảnh ảo $\Leftrightarrow {{\text{{d}'}}_{2}}<0$ khi $0\le {{\text{d}}_{1}}<28$ và d1> 60.
c. Độ phóng đại ảnh của hệ:
\[\text{k}=\frac{\overline{\text{{A}'{B}'}}}{\overline{\text{AB}}}={{\text{k}}_{1}}\text{. }{{\text{k}}_{2}}=\frac{20}{{{\text{d}}_{1}}-20}\frac{8\left( 60-{{\text{d}}_{1}} \right)}{\left( {{\text{d}}_{1}}-28 \right)}\frac{\left( {{\text{d}}_{1}}-20 \right)}{\left( 10{{\text{d}}_{1}}-600 \right)}\]
\[\text{k}=\frac{16}{{{\text{d}}_{1}}-28}.\]
Vì không biết rõ chiều của $\text{{A}'{B}'}$so với AB nên ta viết: \[\frac{\overline{\text{{A}'{B}'}}}{\overline{\text{AB}}}=\pm \frac{8}{2}=\pm 4\]
Giải hai phương trình:
$\frac{16}{{{\text{d}}_{1}}-28}=4\Rightarrow {{\text{d}}_{1}}=32\text{cm }\Leftrightarrow \text{ AB}$ thật.
$\frac{16}{{{\text{d}}_{1}}-28}=-4\Rightarrow {{\text{d}}_{1}}=24\text{cm }\Leftrightarrow \text{ AB}$thật.
Vậy cả 2 giá trị đều thỏa mãn điều kiện AB thật, nhưng theo bảng xét dấu khi d1 =32cm thì $\text{{A}'{B}'}$ là ảnh thật không thỏa mãn điều kiện đầu bài.
Vậy vật cho ảnh ảo cao 8cm ngược chiều với vật AB khi AB cách L1 24cm.