Tổng Hợp Dao Động

TỔNG HỢP DAO ĐỘNG

 

I. BÀI TOÁN TỔNG HỢP HAI DAO ĐỘNG ĐIỀU HÒA CÙNG PHƯƠNG, CÙNG TẦN SỐ

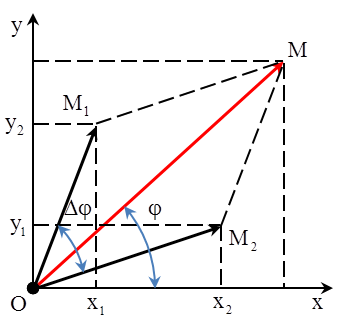
Bài toán: Một vật dao động điều hòa là tổng hợp của hai dao động thành phần cùng phương, cùng tần số có phương trình lần lượt là \[{{x}_{1}}={{A}_{1}}c\text{os}\left( \omega t+{{\varphi }_{1}} \right)\] và \[{{x}_{2}}={{A}_{2}}c\text{os}\left( \omega t+{{\varphi }_{2}} \right)\]. Xác định dao động tổng hợp của vật. 1. Tổng hợp dao động bằng phương pháp vecto quay Theo phương pháp này thì dao động tổng hợp của hai dao động có dạng: \[x=A\cos \left( \omega t+\varphi  \right)\] Trong đó: \[{{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}c\text{os}\Delta \varphi \] Và  \[\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}c\text{os}{{\varphi }_{1}}+{{A}_{2}}c\text{os}{{\varphi }_{2}}}\] Với \[\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}\] là độ lệch pha giữa hai dao động thành phần.

2. Tổng hợp dao động bằng máy tính cầm tay

Để tiến hành tổng hợp hai dao động điều hòa, ta có thể tiến hành như sau: + Bước 1: Chuyển máy tính về số phức Mode \[\to \] 2 + Bước 2: Nhập số liệu Dạng đại số Dạng phức \[{{x}_{1}}={{A}_{1}}c\text{os}\left( \omega t+{{\varphi }_{1}} \right)\] \[{{A}_{1}}\angle {{\varphi }_{1}}\] \[{{x}_{2}}={{A}_{2}}c\text{os}\left( \omega t+{{\varphi }_{2}} \right)\] \[{{A}_{2}}\angle {{\varphi }_{2}}\] + Bước 3: Xuất kết quả Shift \[\to \] 2 \[\to \] 3 \[\to \]=

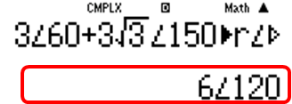
+ Chuyển máy tính về số phức Mode \[\to \] 2 + Xuất kết quả Shift \[\to \] 2 \[\to \] 3 \[\to \]=

 

 

 

II. CÁC BÀI TOÁN LIÊN QUAN:

1. Bài toán liên quan đến khoảng cách giữa hai vật

Hướng dẫn:

+ Ta có, khoảng cách giữa hai vật được xác định bởi \[\Delta x=\left| {{x}_{1}}-{{x}_{2}} \right|\] + Ta thu được : \[\Delta x=\left| 6\cos \left( \frac{5\pi }{3}t+\pi  \right) \right|\]cm Để \[\Delta {{x}_{m\text{ax}}}\]thì \[\frac{5\pi }{3}t+\pi =k\pi \Rightarrow t=\frac{3}{5}\left( k-1 \right)\] Tại \[k=2\] thì \[t=0,6\]s Đáp án C

+ Chuyển máy tính về số phức Mode \[\to \] 2 + Nhập kết quả:   + Xuất kết quả Shift \[\to \] 2 \[\to \] 3 \[\to \]=

2. Bài toán cực trị liên quan đến thay đổi biên độ

Hướng dẫn:

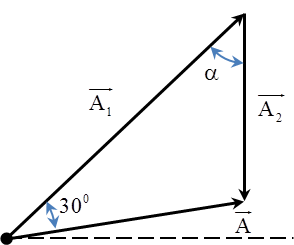
+ Phương pháp đại số Ta có \[{{x}_{2}}=x-{{x}_{1}}\Rightarrow A_{2}^{2}={{A}^{2}}+A_{1}^{2}-2A{{A}_{1}}\cos \left( {{\varphi }_{1}}-\varphi  \right)\] Đạo hàm hai vế với biến là A1 ta thu được \[0=2A{A}'-2A\cos \left( {{\varphi }_{1}}-\varphi  \right)-2{{A}_{1}}{A}'\cos \left( {{\varphi }_{1}}-\varphi  \right)\] \[{A}'\]đạt cực trị tại \[{A}'=0\] từ đó ta tính được \[{{A}_{1}}=A\cos \left( {{\varphi }_{1}}-\varphi  \right)=\frac{\sqrt{3}}{2}A\] Thay vào biểu thức biên độ ta thu được \[{{A}_{max}}=10cm\] Áp dụng định lý sin trong tam giác \[\frac{A}{\sin \alpha }=\frac{{{A}_{2}}}{\sin \left( {{30}^{0}} \right)}\Rightarrow A=\frac{{{A}_{2}}}{\sin \left( {{30}^{0}} \right)}\sin \alpha \] Để Amax thì \[\sin \alpha =1\Rightarrow {{A}_{max}}=\frac{{{A}_{2}}}{\sin \left( {{30}^{0}} \right)}=10cm\]

• Đáp án B

3. Bài toán số lần hai vật gặp nhau

Hướng dẫn:

Hai chất điểm có cùng li độ

\[{{x}_{1}}={{x}_{2}}\Leftrightarrow {{x}_{1}}-{{x}_{2}}=0\Leftrightarrow 6\cos \left( 2\pi t \right)=0\Leftrightarrow 2\pi t=2k\pi \Rightarrow t=k\]

Từ biểu thức của t, ta thấy rằng nếu không tính thời điểm ban đầu thì hai dao động  này gặp nhau lần thứ 5 ứng với \[k=6\Rightarrow t=6s\]

• Đáp án B

 

 

III.BÀI TậP VẬN DỤNG

Câu 1: Xét dao động tổng hợp cuả hai dao động thành phần có cùng phương và cùng tần số. Biên độ của dao động tổng hợp không phụ thuộc

          A. biên độ của dao động thành phần thứ nhất    B. biên độ của dao động thành phần thứ hai

          C. tần số chung của hai dao động thành phần    D. độ lệch pha của hai dao động thành phần

Câu 2: Dao động của một vật là tổng hợp của hai dao động thành phần có phương trình lần lượt là \[{{x}_{1}}=3\cos \left( \pi t \right)\]cm và \[{{x}_{2}}=4\cos \left( \pi t \right)\]cm. Phương trình của dao động tổng hợp:

          A. \[x=3\cos \left( \pi t+\pi  \right)\]cm                                                                  B. \[x=7\cos \left( \pi t \right)\]cm

          C. \[x=3\cos \left( \pi t-\pi  \right)\]cm                                                                  D. \[x=7\cos \left( 2\pi t \right)\]cm

Câu 3: Phương trình dao động tổng hợp của hai dao động thành phần \[{{x}_{1}}=6\cos \left( \pi t+\frac{\pi }{3} \right)\]cm và \[{{x}_{2}}=6\cos \left( \pi t \right)\]cm:

          A. \[x=3\cos \left( \pi t \right)\]cm                                                                  B. \[x=3\cos \left( \pi t+\frac{\pi }{2} \right)\]cm

          C. \[x=6\sqrt{3}\cos \left( \pi t+\frac{\pi }{6} \right)\]cm                                                                  D. \[x=3\sqrt{3}\cos \left( \pi t+\frac{\pi }{2} \right)\]cm

Câu 4: Dao động của một vật là tổng hợp của hai dao động thành phần có biên độ lần lượt là 3 cm và 4 cm. Độ lệch pha giữa chúng là \[\frac{\pi }{2}\]. Dao động tổng hợp có biên độ:

          A. 3 cm                        B. 4 cm                        C. 5 cm      D. 6 cm

Câu 5: Hai dao động thành phần của một chất điểm có phương trình lần lượt là \[{{x}_{1}}=4\cos \left( 2\pi t \right)\]cm và \[{{x}_{2}}=4\cos \left( 2\pi t+\frac{\pi }{2} \right)\]cm. Tốc độ của chất điểm này khi nó đi qua vị trí cân bằng là:

          A. 8π cm/s                    B. \[4\sqrt{2}\pi \] cm/s C. \[8\sqrt{2}\pi \]cm/s                D. 4π cm/s

Câu 6: Hai dao động thành phần của một vật dao động điều hòa có phương trình lần lượt là \[{{x}_{1}}=5\cos \left( \pi t+\frac{\pi }{6} \right)\] cm và \[{{x}_{2}}=5\cos \left( \pi t+\frac{\pi }{3} \right)\]cm. Gia tốc của vật khi vật đang ở biên âm gần giá trị nào sau đây nhất

          A. 50 cm/s²                  B. 100 cm/s²                 C. 150 cm/s²  D. 200 cm/s²               

Câu 7: Dao động tổng hợp của hai dao động thành phần có dạng \[x=5\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm. Xác định dao động thành phần \[{{x}_{1}}\] biết rằng \[{{x}_{2}}=5\cos \left( 2\pi t+\frac{2\pi }{3} \right)\]cm.

          A. \[{{x}_{1}}=5\sqrt{3}\cos \left( 2\pi t+\frac{\pi }{6} \right)\]cm                              B. \[{{x}_{1}}=5\cos \left( 2\pi t \right)\]cm

          C. \[{{x}_{1}}=10\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm                                                                  D. \[{{x}_{1}}=5\sqrt{3}\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm

Câu 8: Dao động cuả một vật là tổng hợp của hai dao động thành phần \[{{x}_{1}}=6\cos \left( 4\pi t \right)\]cm và \[{{x}_{2}}=3\cos \left( 4\pi t+\pi  \right)\]cm. Tốc độ của vật taị vị trí vật có động năng bằng 3 lần thế năng là:

          A. \[6\sqrt{3}\pi \]cm/s B. 6π cm/s                    C. 3π cm/s   D. \[3\sqrt{3}\pi \]cm/s

Câu 9: Cho hai dao động thành phần \[{{x}_{1}}=2\cos \left( \pi t \right)\] cm và \[{{x}_{2}}={{A}_{2}}\cos \left( \pi t+\frac{2\pi }{3} \right)\] cm. Giá trị của A₂ để biên độ A của dao động tổng hợp cực tiểu là:

          A. 1 cm                        B. 2 cm                        C. \[\sqrt{2}\]cm                         D. \[\sqrt{3}\]cm

Câu 10: Trong tổng hợp hai dao động thành phần \[{{x}_{1}}={{A}_{1}}\cos \left( \omega t \right)\] và \[{{x}_{2}}={{A}_{2}}\cos \left( \omega t+\varphi  \right)\] ta thu được \[x=A\cos \left( \omega t+\theta  \right)\]. Giá trị của φ để A cực đại:

          A. 0                             B. \[\frac{\pi }{2}\]      C. π        D. 3π

Câu 11: Ta có thể tổng hợp hai dao động thành phần khi hai dao động này:

          A. cùng phương, cùng tần số

          B. cùng biên độ và cùng tần số

          C. cùng tần số và có độ lệch pha không đổi      

          D. cùng phương, cùng tần số và có độ lệch pha không đổi theo thời gian

Câu 12: Chọn phát biểu sai: Trong tổng hợp dao động. Biên độ của dao động tổng hợp

          A. cực đại khi độ lệch pha giữa hai dao động thành phần là 2π

          B. cực tiểu khi độ lệch pha giữa hai dao động thành phần là π

          C. phụ thuộc vào tần số của hai dao động thành phần

          D. phụ thuộc và độ lệch pha giữa hai dao động thành phần

Câu 13: Biểu thức xác định pha ban đầu của dao động tổn hợp từ hai dao động thành phần:

          A. \[\tan \varphi =\frac{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}\]                               B. \[\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}\]

          C. \[\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}\]                               D. \[\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}\]

Câu 14: A₁, A₂ lần lượt là biên độ của các dao động thành phần. Gọi A là biên độ dao động tổng hợp. Điều kiện của độ lệch pha Δφ để \[A=\left| {{A}_{1}}-{{A}_{2}} \right|\]là:

          A. \[\Delta \varphi =2k\pi \]                              B. \[\Delta \varphi =\left( 2k+1 \right)\pi \]                                   C. \[\Delta \varphi =k\pi \]                        D.\[\Delta \varphi =\left( k+1 \right)\pi \]

Câu 15: (Quốc giá – 2014) Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là \[{{x}_{1}}={{A}_{1}}\cos \left( \omega t+0,35 \right)\]cm và \[{{x}_{2}}={{A}_{2}}\cos \left( \omega t-1,57 \right)\]cm. Dao động tổng hợp của hai dao động này có phương trình \[x=20\cos \left( \omega t+\varphi  \right)\]cm. Giá trị cực đại của \[\left( {{A}_{1}}+{{A}_{2}} \right)\] gần giá trị nào sau đây nhất?

          A. 20 cm                      B. 25 cm                      C. 35 cm      D. 40 cm

Câu 16: Hai dao động cùng phương lần lượt có phương trình \[{{x}_{1}}={{A}_{1}}\cos \left( \pi t+\frac{\pi }{6} \right)\]cm và \[{{x}_{2}}=6\cos \left( \pi t-\frac{\pi }{2} \right)\]cm. Dao động tổng hợp của hai dao động này có phương trình \[x=10\cos \left( \omega t+\varphi  \right)\]. Thay đổi A₁ đến khi biên độ A đạt giá trị cực tiểu. Khi đó giá trị của φ là:

          A. \[-\frac{\pi }{6}\]    B. \[-\frac{\pi }{3}\]     C. π        D. 0

Câu 17: Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số có dạng như sau \[{{x}_{1}}=\cos \left( 4t+{{\varphi }_{1}} \right)\] cm, \[{{x}_{2}}=2\cos \left( 4t+{{\varphi }_{2}} \right)\] cm (t tính bằng s), với \[0\le {{\varphi }_{1}}-{{\varphi }_{2}}\le \pi \] . Biết phương trình dao động tổng hợp là \[x=\cos \left( 4t+\frac{\pi }{6} \right)\] cm. Giá trị φ₁ bằng:

          A. \[-\frac{\pi }{6}\]     B. \[\frac{2\pi }{3}\]     C. \[-\frac{5\pi }{6}\]                      D. \[\frac{\pi }{2}\]

Câu 18: Hai vật dao động trên trục Ox có phương trình \[{{x}_{1}}=3\cos \left( 5\pi t-\frac{\pi }{3} \right)\]cm và \[{{x}_{2}}=\sqrt{3}\cos \left( 5\pi t-\frac{\pi }{6} \right)\]cm thì sau 1 s kể từ thời điểm t = 0 số lần hai vật đi ngang qua nhau là:

          A. 5                             B. 6                              C. 7        D. 8

Câu 19: Một chất điểm tham gia đồng thời hai dao động điều hòa trên trục Ox có phương trình \[{{x}_{1}}={{A}_{1}}\cos \left( 10t \right)\] và \[{{x}_{2}}={{A}_{2}}\cos \left( 10t+{{\varphi }_{2}} \right)\]. Phương trình dao động tổng hợp \[x={{A}_{1}}\sqrt{3}\cos \left( 10t+\varphi  \right)\] trong đó \[{{\varphi }_{2}}-\varphi =\frac{\pi }{6}\]. Tỉ số \[\frac{\varphi }{{{\varphi }_{2}}}\] bằng:

          A. \[\frac{2}{3}\] hoặc \[\frac{4}{3}\]             B. \[\frac{1}{3}\] hoặc \[\frac{2}{3}\]                            C. \[\frac{1}{2}\] hoặc \[\frac{3}{4}\]                            D. \[\frac{3}{4}\] hoặc \[\frac{2}{5}\]

Câu 20: Dao động của vật là tổng hợp của hai dao động thành phần cùng phương, cùng tần số\[{{x}_{1}}=4,8\cos \left( 10\sqrt{2}t+\frac{\pi }{2} \right)\]cm, \[{{x}_{2}}={{A}_{2}}\cos \left( 10\sqrt{2}t-\pi  \right)\]cm. Biết tốc độ của vật tại thời điểm động năng bằng 3 lần thế năng là \[0,3\sqrt{6}\]m/s. Biên độ A₂ bằng:

          A. 7,2 cm                     B. 6,4cm                      C. 3,2 cm      D. 3,6 cm

 

 

ĐÁP ÁN

1.C	2.B	3.C	4.C	5.C	6.B	7.B	8.A	9.A	10.A
11.D	12.C	13.C	14.B	15.C	16.B	17.C	18.A	19.C	20.D

Bài viết gợi ý: