Ví dụ 1: Cho hình biết \[\widehat{BAC}={{130}^{0}}\], \[\widehat{ACD}={{50}^{0}}\]. Chứng minh AB // CD
Hướng dẫn giải:
Chúng ta đã biết rằng :
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
Do vậy, ta cần tạo ra một cặp góc so le trong hoặc một cặp góc đồng vị mà sẽ chứng minh được cặp góc đó bằng nhau. Điều này gợi ta nghĩ đến vẽ thêm yếu tố phụ là tia đối của tia AB, hoặc tia đối của tia AC, hoặc tia đối của tia CA, hoặc tia đối của tia CD.
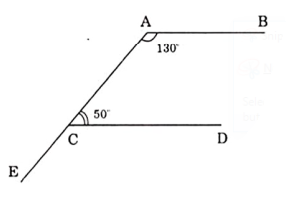
Lời giải:
Vẽ tia CE là tia đối của tia CA
Ta có : \[\widehat{ACD}\]+ \[\widehat{DCE}\]=1800 (hai góc \[\widehat{ACD}\] và\[\widehat{DCE}\] kề bù )
\[\Rightarrow \]\[\widehat{DCE}\]= 1800 - \[\widehat{ACD}\]= 1300
Ta có \[\widehat{DCE}\]=\[\widehat{BAC}\] mà \[\widehat{DCE}\]và\[\widehat{BAC}\] là hai góc đồng vị
Do đó AB // CD
Ví dụ 2:
Trên hình bên cho hai đường thẳng xy và x’y’ phân biệt.
Hãy nêu cách nhận biết xem hai đường thẳng xy và x’y’ song song hay cắt nhau x’ y’ bằng dụng cụ thước đo góc ?
Hướng dẫn giải:
Chúng ta đã biết hai đường thẳng phân biệt thì hoăc cắt nhau hoặc song song. Hơn nữa để nhận biết hai đường thẳng có song song với nhau hay không ta đã có tính chất thừa nhận sau : Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
Do vậy lấy điểm A trên xy, điểm B trên x’y’ ta có đường thẳng AB là yếu tố phụ cần vẽ thêm để làm xuất hiện các cặp góc so le trong, các cặp góc đồng vị, từ đó tìm ra lời giải bài toán.
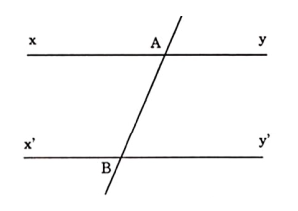
Lời giải:
Lấy điểm A trên đường thẳng xy, B trên đường thẳng x’y’
Vẽ đường thẳng AB. Dùng thước đo góc để đo các góc xAB và ABy’
Có hai trường hợp xảy ra:
1) \[\widehat{xAB}=\widehat{ABy'}\]
Vì \[\widehat{xAB}\] và \[\widehat{ABy'}\] so le trong nên xy // x’y’
2) \[\widehat{xAB}\ne \widehat{ABy'}\]
Vì \[\widehat{xAB}\] và \[\widehat{ABy'}\] so le trong nên xy và x’y’ không song song với nhau
\[\Rightarrow \] Hai đường thẳng xy và x’y’ cắt nhau







