Ví dụ 1: Cho hai góc kề bù xOy và yOx’. Vẽ tia phân giác Oz của góc xOy. Trên nửa mặt phẳng bờ xx’ có chứa tia Oy vẽ tia Oz’ vuông góc với tia Oz.
Chứng tỏ rằng tia Oz’ là tia phân giác của góc yOx’.
Hướng dẫn giải:
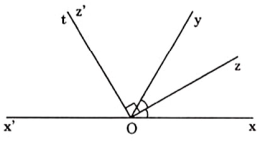
Hai góc xOy và yOx’ kề bù. Oz là tia phân giác của góc xOy và hai tia Oz và Oz’ vuông góc với nhau.
Vẽ thêm đường phụ là tia phân giác Ot của góc yOx’ và chứng minh được hai tia Ot và Oz’ trùng nhau ta sẽ giải được bài toán.
Lời giải:
Vẽ tia Ot là tia phân giác của góc yOx’. Hai tia Oz và Ot lần lượt là hai tia phân giác của hai góc kề bù xOy và yOx’ do đó Oz ⊥ Ot. Mà theo đầu bài ta có Oz ⊥ Oz’ nên hai tia Ot và Oz’ trùng nhau.
Vậy Oz’ là tia phân giác của góc yOx’.
Ví dụ 2: Cho góc xOy nhọn. Trên nửa mặt phẳng chứa tia Oy có bờ là đường thẳng chứa tia Ox, vẽ tia Oz vuông góc với tia Oy, trên nửa mặt phẳng kia vẽ tia Ot vuông góc với tia Ox. Gọi Om là tia phân giác của góc xOy, On là tia phân giác của góc zOt.
Chứng minh rằng hai tia Om và On là hai tia đối nhau.
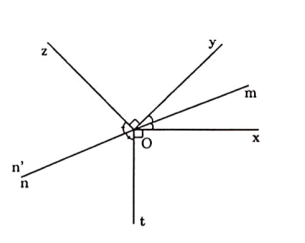
Hướng dẫn giải:
Phương pháp giải bài toán 2 sẽ thích hợp cho việc giải bài toán này. Vẽ đường phụ là tia On’ là tia đối của tia Om và chỉ còn chứng minh hai tia On và On’ trùng nhau.
Lời giải:
Vẽ tia On’ là tia đối của tia Om
Hai tia Om và Ot thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng chứa tia Ox nên tia Ox nên tia Ox nằm giữa hai tia Om và Ot
Ta có: \[\widehat{mOt}=\widehat{xOm}+\widehat{tOx}=\widehat{xOm}+{{90}^{0}}\]
\[\widehat{mOt}+\widehat{n'Ot}={{180}^{0}}\](hai góc kề bù)
\[\Rightarrow \widehat{n'Ot}={{180}^{0}}-\widehat{mOt}={{180}^{0}}-(\widehat{xOm}+{{90}^{0}})={{90}^{0}}-\widehat{xOm}\](1)
Chứng minh tương tự ta cũng có: \[\widehat{zOn'}={{90}^{0}}-\widehat{mOy}\](2)
Mà \[\widehat{xOm}=\widehat{mOy}\] ( Om là tia phân giác \[\widehat{xOy}\]) (3)
Từ (1), (2), (3) ta có \[\widehat{n'Ot}=\widehat{zOn'}\]
Mà tia On’ nằm giữa hai tia Ot và Oy nên On’ là tia phân giác của góc zOt
Vậy hai tia On và On’ trùng nhau
Suy ra hai tia Om và On là hai tia đối







