Ví dụ 1: Cho hình biết \[\widehat{ACB}>\widehat{xAC}\], Ax // By. Chứng minh \[\widehat{ACB}=\widehat{xAC}+\widehat{CBy}\]
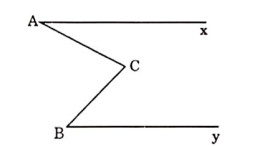
Lời giải:
Trên nửa mặt phẳng bờ AC có chứa tia CB vẽ tia Cz sao cho \[\widehat{xAC}\]=\[\widehat{ACz}\]
Ta có: \[\widehat{ACz}=\widehat{xAC}\], \[\widehat{xAC}\] và \[\widehat{ACz}\] so le trong, suy ra Ax // Cz
Trên nửa mặt phẳng bờ AC có \[\widehat{ACz}<\widehat{ACB}\]( Vì \[\widehat{ACB}>\widehat{xAC}\],\[\widehat{ACz}=\widehat{xAC}\]) nên tia Cz nằm giữa hai tia CA và CB
Do đó \[\widehat{ACB}=\widehat{ACz}+\widehat{zCB}\]
Mặt khác : Ax // Cz, Ax // By\[\Rightarrow \] By // Cz
By // Cz \[\Rightarrow \] \[\widehat{zCB}=\widehat{CBy}\]
Do đó \[\widehat{ACB}=\widehat{xAC}+\widehat{CBy}\]
Ví dụ 2: Chứng minh rằng: Nếu hai góc nhọn \[\widehat{xOy}\]và \[\widehat{x'Oy'}\] có Ox // O’x’, Oy // O’y’ thì \[\widehat{xOy}=\widehat{x'Oy'}\]
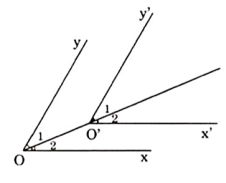
Lời giải: Vẽ tia OO’ ta có:
\[\widehat{{{O}_{1}}}=\widehat{O{{'}_{1}}}\] ( \[\widehat{{{O}_{1}}}\] và \[\widehat{O{{'}_{1}}}\] đồng vị; Oy // O’y’)
\[\widehat{{{O}_{2}}}=\widehat{O{{'}_{2}}}\] ( \[\widehat{{{O}_{2}}}\] và \[\widehat{O{{'}_{2}}}\] đồng vị; Ox // O’x’)
Suy ra \[\widehat{{{O}_{1}}}+\widehat{{{O}_{2}}}=\widehat{O{{'}_{1}}}+\widehat{O{{'}_{2}}}\]
Hay \[\widehat{xOy}=\widehat{x'Oy'}\]
Lưu ý: Nếu thay giả thiết “hai góc nhọn” bởi “hai góc tù” và giải tương tự như trên ta cũng có \[\widehat{xOy}=\widehat{x'Oy'}\]. Hai góc \[\widehat{xOy}\], \[\widehat{x'Oy'}\] gọi là hai góc có cạnh tương ứng song song.







