Tét for fun
Cho \[x,\text{ }y\] thỏa mãn $\sqrt{2x+3}+\sqrt{y+3}=4.$ Tìm giá trị nhỏ nhất của $P=\sqrt{x+2}+\sqrt{y+9}$.
Tính số nghiệm của phương trình \[\cot x={{2}^{x}}\] trong khoảng \[\left( \frac{11\pi }{12};2019\pi \right)\].
Cho hàm số $y={{x}^{3}}+3{{x}^{2}}$ có đồ thị $\left( C \right)$ và điểm $M\left( m;0 \right)$ sao cho từ M vẽ được ba tiếp tuyến đến đồ thị $\left( C \right)$, trong đó có hai tiếp tuyến vuông góc với nhau. Khi đó khẳng định nào sau đây đúng.
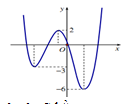
Hình vẽ bên là đồ thị của hàm số $y=f\left( x \right).$ Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số $y=\left| f\left( x-1 \right)+m \right|$ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
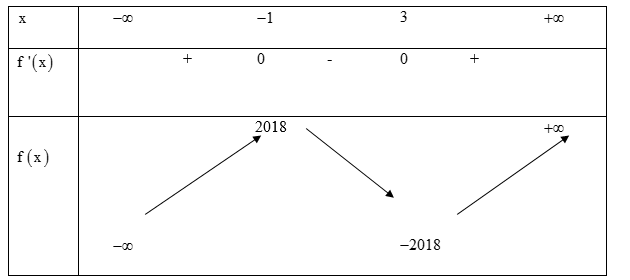
Cho $f\left( x \right)$ là một hàm số liên tục trên đoạn $\left[ -1;8 \right]$, biết $f\left( 1 \right)=f\left( 3 \right)=f\left( 8 \right)=2$ có bảng biến thiên như sau:
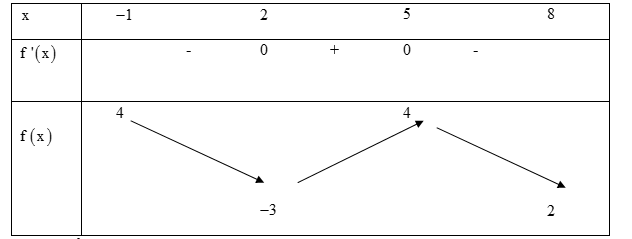
Tìm m để phương trình $f\left( x \right)=f\left( m \right)$ có ba nghiệm phân biệt thuộc đoạn $\left[ -1;8 \right].$
Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên R. Bảng biến thiên của hàm số $y=f'\left( x \right)$ được cho như hình vẽ bên. Hàm số $y=f\left( 1-\frac{x}{2} \right)+x$ nghịch biến trên khoảng ?
.png)
Gọi ${{m}_{1}},{{m}_{2}}$là các giá trị của tham số m để đồ thị hàm số $y=2{{x}^{3}}-3{{x}^{2}}+m-1$ có hai điểm cực trị B, C sao cho tam giác OBC có diện tích bằng 2, với O là gốc tọa độ. Tính ${{m}_{1}}.{{m}_{2}}.$
Cho hàm số $y=\frac{4x-3}{x-3}$có đồ thị $\left( C \right)$. Biết đồ thị $\left( C \right)$có hai điểm phân biệt M, N và khoảng cách từ M hoặc N đến hai đường tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng:
Cho hàm số$f\left( x \right)$xác định trên R và hàm số $y=f'\left( x \right)$có đồ thị như hình bên dưới:
Xét các khẳng định sau:
(I) Hàm số$y=f\left( x \right)$có ba cực trị.
(II) Phương trình $f\left( x \right)=m+2018$có nhiều nhất ba nghiệm.
(III) Hàm số$y=f\left( x+1 \right)$nghịch biến trên khoảng $\left( 0;1 \right)$.
Số khẳng định
đúng là: 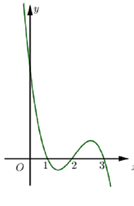
Cho hàm số$y=f\left( x \right)$ có đạo hàm$f'\left( x \right)={{x}^{2}}\left( x-1 \right){{\left( x-4 \right)}^{2}}$. Khi đó số điểm cực trị của hàm số$y=f\left( {{x}^{2}} \right)$ là
Cho hàm số bậc ba $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ bên dưới:
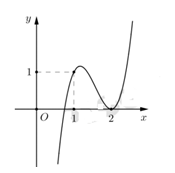
Hỏi
đồ thị hàm số $g\left( x \right)=\frac{\left( {{x}^{2}}-3x+2
\right)\sqrt{x-1}}{x\left[ {{f}^{2}}\left( x \right)-f\left( x \right)
\right]}$ có bao nhiêu đường tiệm cận đứng ?
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y={{e}^{\frac{3x-\sqrt{m{{x}^{2}}+1}}{x-\sqrt{\left( 2018-m \right){{x}^{2}}+1}}}}$ có 2 tiệm cận ngang?
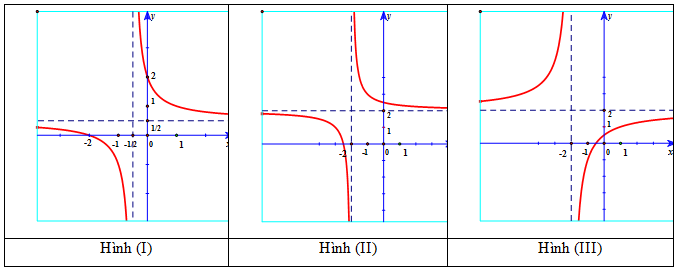
Cho hàm số $y=\frac{mx+1}{x+m}$, với m là tham số. Các hình nào dưới đây không thể là đồ thị của hàm số đã cho với mọi $m\in \mathbb{R}$?
Có bao nhiêu giá trị nguyên của tham số m để phương trình $\cos 2x=m\sqrt{1+\tan x}.{{\cos }^{2}}x$ có nghiệm thuộc đoạn \[\text{ }\!\![\!\!\text{ 0;}\frac{\pi }{3}\text{ }\!\!]\!\!\text{ }\]?
Cho hàm số $y=f\left( x \right)$có bảng biến thiên như sau.
Đồ thị hàm số \[y=\left| f\left( \text{x}-2017 \right)+2018 \right|\] có bao nhiêu điểm cực trị?
Gọi S là tập hợp tất cả các giá trị của tham số m sao cho GTNN của hàm số $y=\left| {{\sin }^{4}}x+\cos 2x+m \right|$ bằng 2. Số phần tử của S là
Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$
được cho như hình vẽ bên. Hàm số $y=f\left( \operatorname{cosx} \right)+{{x}^{2}}-x$
đồng biến trên khoảng:
.png)
Cho hai hàm số đa thức bậc bốn $y=f(x)$ và $y=g(x)$có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số $y=f(x)$. Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là $-3$ và cắt nhau tại hai điểm nữa có hoành độ lần lượt là $-1$ và $3$. Tìm tập hợp tất cả các giá trị thực của tham số $m$ để bất phương trình $f(x)\ge g(x)+m$ nghiệm đúng với mọi $x\in \text{ }\!\![\!\!\text{ }-3;3]$.
.png)
Cho các số thực dương \[x,y.\] Tìm giá trị lớn nhất của biểu thức $P=\frac{4x{{y}^{2}}}{{{\left( x+\sqrt{{{x}^{2}}+4{{y}^{2}}} \right)}^{3}}}$.
Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính đầu mép dưới của màn hình).
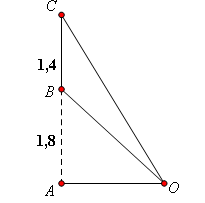
Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó.
Xét các số thực dương x, y thỏa mãn ${{\log }_{\sqrt{3}}}\frac{x+y}{{{x}^{2}}+{{y}^{2}}+xy+2}=x\left( x-3 \right)+y\left( y-3 \right)+xy.$ Tìm giá trị ${{P}_{m\text{ax}}}$ của biểu thức $P=\frac{3x+2y+1}{x+y+6}$.
Số các giá trị nguyên của tham số m để phương trình ${{\log }_{\sqrt{2}}}\left( x-1 \right)={{\log }_{2}}\left( mx-8 \right)$ có hai nghiệm thực phân biệt là :
Cho hàm số \[f\left( x \right)=\ln \left( 1-\frac{1}{{{x}^{2}}} \right).\] Biết rằng \[f\left( 2 \right)+f\left( 3 \right)+...+f\left( 2018 \right)=\ln a-\ln b+\ln c-\ln d\] với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và \[a
Có bao nhiêu giá trị nguyên của tham số m để phương trình \[{{\log }_{\sqrt{3}}}(x-1)+{{\log }_{\frac{1}{3}}}(mx-8)={{\log }_{2}}\left( 2+\sqrt{3} \right)+{{\log }_{2}}\left( 2-\sqrt{3} \right)\] có hai nghiệm thực phân biệt?
Phương trình $2{{\log }_{3}}\left( \cot x \right)={{\log }_{2}}\left( \cos x \right)$ có bao nhiêu nghiệm trong
khoảng 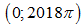 ?
?
Cho các số thực $x,\,y$ dương và thỏa mãn $lo{{g}_{2}}\frac{{{x}^{2}}+{{y}^{2}}}{3xy+{{x}^{2}}}+{{2}^{{{\log }_{2}}({{x}^{2}}+2{{y}^{2}}+1)}}\le {{\log }_{2}}{{8}^{xy}}$. Tìm giá trị nhỏ nhất của biểu thức $P=\frac{2{{x}^{2}}-xy+2{{y}^{2}}}{2xy-{{y}^{2}}}$.
Tìm tất cả các giá trị của tham số $m$
để hàm số $y=\ln \left( 16{{x}^{2}}+1 \right)-\left( m+1 \right)x+m+2$ nghịch
biến trên khoảng 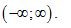
Gọi \[x,y\] là các số thực dương thỏa mãn điều kiện \[{{\log }_{9}}x={{\log }_{6}}x={{\log }_{4}}(x+y)\] và \[\frac{x}{y}=\frac{-a+\sqrt{b}}{2}\], với \[a,b\] là hai số nguyên dương. Tính \[a+b\].
Tìm $m$ để bất phương trình ${{2}^{x}}+{{3}^{x}}+{{4}^{x}}+{{5}^{x}}\ge 4+mx$ có tập nghiệm là $\mathbb{R}$.
Cho x, y là số thực dương thỏa mãn ${{\log }_{2}}x+{{\log }_{2}}y+1\ge {{\log }_{2}}\left( {{x}^{2}}+2y \right).$ Tìm giá trị nhỏ nhất của $P=x+2y$
Cho hình lăng trụ tam giác $ABC.{A}'{B}'{C}'$ có đáy là tam giác đều cạnh a. Gọi M là trung điểm của ${B}'{C}'$, biết $A{B}'\bot {A}'M$ và $A{B}'=AM$. Cạnh bên $A{A}'$ tạo với đáy một góc bằng $60{}^\circ $. Tính tang của góc giữa hai mặt phẳng $\left( BC{C}'{B}' \right)$ và $\left( {A}'{B}'{C}' \right)$.
Cho bát diện đều $ABCDEF$ có cạnh bằng 1. Dựng điểm ${E}'$ sao cho $\overrightarrow{BA}=\overrightarrow{E{E}'}$, ${B}'$ là điểm đối xứng với $B$ qua trung điểm của cạnh $DE$. Thể tích của khối đa diện $BF{B}'E{E}'A$ bằng.
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng \[1\]. Cắt hình lập phương bằng một mặt phẳng đi qua đường chéo $BD'$. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được.
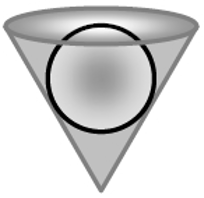
Thả một quả cầu đặc có bán kính 3 $\left( \text{cm} \right)$ vào một vật hình nón (có đáy nón không kín) (như hình vẽ bên). Cho biết khoảng cách từ tâm quả cầu đến đỉnh nón là 5 $\left( \text{cm} \right)$. Tính thể tích (theo đơn vị cm3) phần không gian kín giới hạn bởi bề mặt quả cầu và bề mặt trong của vật hình nón.
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều, $SC=SD=a\sqrt{3}$. Tính thể tích $V$ của khối chóp $S.ABCD$ theo $a$.
Trên một hình tròn là đáy chung, ta dựng hai hình nón (hình nón này chứa hình nón kia – như hình vẽ), sao cho hai đỉnh cách nhau bằng $a$. Góc ở đỉnh hình nón lớn là $2\alpha $ và của hình nón nhỏ là $2\beta $. Khi đó thể tích phần ở ngoài hình nón nhỏ và ở trong hình nón to là bao nhiêu?
.png)
Cho
điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao
cho $\frac{SM}{MA}=\frac{1}{2};\frac{SN}{NB}=2.$ Mặt phẳng 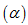 đi qua MN và song song với SC chia
khối chóp thàng 2 phần. Gọi \[{{V}_{1}}\] là thể tích của khối đa diện chứa \[A,\text{
}{{V}_{2}}\] là thể tích của khối đa diện còn lại. Tính tỉ số $\frac{{{V}_{1}}}{{{V}_{2}}}$.
đi qua MN và song song với SC chia
khối chóp thàng 2 phần. Gọi \[{{V}_{1}}\] là thể tích của khối đa diện chứa \[A,\text{
}{{V}_{2}}\] là thể tích của khối đa diện còn lại. Tính tỉ số $\frac{{{V}_{1}}}{{{V}_{2}}}$.
Cho hình lập phương $ABCD.A'B'C'D'$ có tất cả các cạnh bằng 1. Gọi M là trung điểm của $BB'.$ Tính thể tích khối $A'MCD.$
.png)
Cho hình chóp $S.ABCD$ có đáy là hình bình hành và có thể tích bằng $48$. Trên cạnh $SB$, $SD$ lấy các điểm $M$, $N$ sao cho $SM=MB$, $SD=3SN$. Mặt phẳng $\left( AMN \right)$ cắt $SC$ tại $P$. Tính thể tích $V$ của khối tứ diện $SMNP$.
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho $B'M=\frac{1}{2}A'B'.$ Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích ${{V}_{1}}$ và khối đa diện chứa đỉnh C’ có thể tích ${{V}_{2}}.$ Tính $\frac{{{V}_{1}}}{{{V}_{2}}}.$
Cho hình lập phương \[ABCD.ABCD\] có cạnh bằng \[a\]. Điểm \[M\] thuộc đoạn thẳng \[BC\], điểm N thuộc đoạn thẳng \[MN=\frac{2a}{\sqrt{5}+1}\] tạo với mặt phẳng đáy một góc \[30{}^\circ \]. Tìm độ dài nhỏ nhất của đoạn thẳng \[MN\].
Cho hình chóp S.ABCD, G là điểm nằm trong tam giác SCD, E, F lần lượt là trung điểm của AB và AD. Thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( E\,FG \right)$là:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có $AB=2\sqrt{3}$ và AA’=2. Gọi M và N lần lượt là trung điểm của A’C’ và A’B’ (như hình vẽ bên). Tính cosin của góc tạo bởi hai mặt phẳng (AB’C’) và (BCMN).
.png)
Cho hình nón đỉnh $S$ ,đáy là đường tròn $\left( O;r \right)$ . Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm $A$ và $B$ sao cho $SA=AB=\frac{8r}{5}$ . Tính theo r khoảng cách từ O đến $\left( SAB \right)$
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều cạnh \[a\], cạnh bên \[SA\] vuông góc với mặt đáy, \[SA=2a\]. Gọi \[M\] là trung điểm của \[SC\]. Tính côsin của góc \[\alpha \] là góc giữa đường thẳng \[BM\] và mặt phẳng \[\left( ABC \right)\].
Tính
tổng tất cả các nghiệm của phương trình \[sin\text{ }2x+4sin\text{
}x-2cos\text{ }x-4=0\] trong đoạn 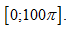 của phương trình:
của phương trình:
Gọi S là tổng các nghiệm của phương trình $\frac{\operatorname{s}\text{inx}}{\cos
x+1}=0$ trên đoạn 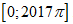 .Tính S.
.Tính S.
Hệ số ${{x}^{6}}$ khi khai triển đa thức $P\left( x \right)={{\left( 5-3x \right)}^{10}}$ có giá trị bằng đại lượng nào sau đây?
Tìm tất cả các số tự nhiên k sao cho $C_{14}^{k},C_{14}^{k+1},C_{14}^{k+2}$ theo thứ tự lập thành một cấp số cộng.
Giải bóng truyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm trong hai bảng khác nhau bằng
Tét for fun
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm