Bài Tập Động Lực Học

BÀI TẬP ĐỘNG LỰC HỌC CHẤT ĐIỂM (P1)

 

Hướng dẫn

                                          

Khi gắn vật lò xo dài thêm đoạn l. Ở vị trí cân bằng

                 \[\left| \overrightarrow{{{F}_{0}}} \right|=\left| \overrightarrow{P} \right|\Leftrightarrow k\Delta l=mg\]      

Với lò xo 1: \[k\Delta {{l}_{1}}={{m}_{1}}g\]         (1)                                                               

Với lò xo 1: \[k\Delta {{l}_{2}}={{m}_{2}}g\]       (2)

Lập tỷ số (1), (2) ta được                             

                \[\frac{{{k}_{1}}}{{{k}_{2}}}=\frac{{{m}_{1}}}{{{m}_{2}}}.\frac{\Delta {{l}_{2}}}{\Delta {{l}_{1}}}=2\]        

Hướng dẫn

         

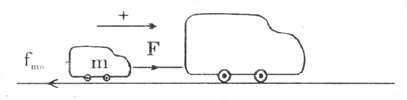
Chọn hướng và chiều như hình vẽ                

Ta có gia tốc của xe là:

\[a=\frac{v-{{v}_{0}}}{t}=0,1m/{{s}^{2}}\]

Theo định luật II Newtơn :  \[\overrightarrow{F}+\overrightarrow{{{F}_{ms}}}=m\overrightarrow{a}\]

                                         \[\Rightarrow F={{F}_{ms}}+ma=200N\]

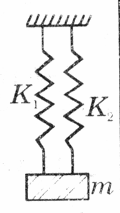
Hướng dẫn

                   

Khi cân bằng: F₁ + F₂ = P

Với  \[{{F}_{1}}={{k}_{1}}\Delta l\] và   \[{{F}_{2}}={{k}_{2}}\Delta l\]        

nên  \[({{k}_{1}}+{{k}_{2}})\Delta l=P\]    

\[\Rightarrow \Delta l=\frac{P}{{{k}_{1}}+{{k}_{2}}}=0,04m\]

Vậy chiều dài của lò xo là: 

\[L={{l}_{0}}+\Delta l=24cm\]  

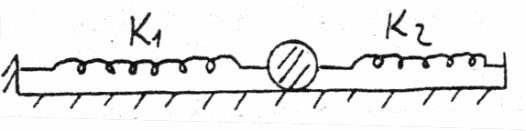
Hướng dẫn

 

Hướng và chiều như hình vẽ:

Khi kéo vật ra khỏi vị trí cân bằng một đoạn x thì :

Độ dãn lò xo 1 là x, độ nén lò xo 2 là x

Tác dụng vào vật gồm 2 lực đàn hồi \[{{\overrightarrow{F}}_{1}};\overrightarrow{{{F}_{2}}}\]

                    \[\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}\]  

Chiếu lên trục Ox ta được :

                  \[F=-{{F}_{1}}-{{F}_{2}}=-({{k}_{1}}+{{k}_{2}})x\]        

Vậy độ cứng của hệ ghép lò xo theo cách trên là:

                      \[k={{k}_{1}}+{{k}_{2}}\]    

Hướng dẫn

         

Đối với vật A ta có:

                \[\overrightarrow{{{P}_{1}}}+\overrightarrow{{{N}_{1}}}+\overrightarrow{F}+\overrightarrow{{{T}_{1}}}+\overrightarrow{{{F}_{ms1}}}={{m}_{1}}\overrightarrow{{{a}_{1}}}\]  

Chiếu xuống Ox ta có: F - T₁ - F_ms1 = m₁a₁

Chiếu xuống Oy ta được: -m₁g + N₁ = 0

Với F_ms1 = kN₁ = km₁g

          F - T₁ - k m₁g = m₁a₁                                     (1)

* Đối với vật B:

        \[\overrightarrow{{{P}_{2}}}+\overrightarrow{{{N}_{2}}}+\overrightarrow{F}+\overrightarrow{{{T}_{2}}}+\overrightarrow{{{F}_{ms2}}}={{m}_{2}}\overrightarrow{{{a}_{2}}}\] 

Chiếu xuống Ox ta có:  T₂ - F_ms2 = m₂a₂

Chiếu xuống Oy ta được: -m₂g + N₂ = 0

Với F_ms2 = k N₂ = k m₂g

   T₂ - k m₂g = m₂a₂     (2)

Vì T₁ = T₂ = T và a₁ = a₂ = a nên:

              F - T - k m₁g = m₁a        (3)

             T - k m₂g = m₂a      (4)

Cộng (3) và (4) ta được  F - k(m₁ + m₂)g = (m₁+ m₂)a  

\[\Rightarrow a=\frac{F-\mu ({{m}_{1}}+{{m}_{2}})g}{{{m}_{1}}+{{m}_{2}}}=1m/{{s}^{2}}\]

Hướng dẫn

 

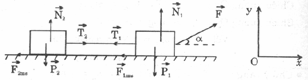
Vật 1 có :

\[\overrightarrow{{{P}_{1}}}+\overrightarrow{{{N}_{1}}}+\overrightarrow{F}+\overrightarrow{{{T}_{1}}}+\overrightarrow{{{F}_{ms1}}}={{m}_{1}}\overrightarrow{{{a}_{1}}}\]

Chiếu xuống Ox ta có: F.cos 30₀ - T₁ - F_ms1 = m₁a₁

Chiếu xuống Oy         : Fsin 30₀ - P₁ + N₁ = 0

Và F_ms1 = k N₁ = k(mg - Fsin 30₀)

F.cos 30₀ - T₁k(mg - Fsin 30₀) = m₁a₁     (1)

Vật 2:

\[\overrightarrow{{{P}_{2}}}+\overrightarrow{{{N}_{2}}}+\overrightarrow{F}+\overrightarrow{{{T}_{2}}}+\overrightarrow{{{F}_{ms2}}}={{m}_{2}}\overrightarrow{{{a}_{2}}}\]

Chiếu xuống Ox ta có:   T - F_ms2 = m₂a₂

Chiếu xuống Oy         :   -P₂ + N₂ = 0

Mà F_ms2 = k N₂ = km₂g

T₂ - k m₂g = m₂a₂

Hơn nữa vì m₁ = m₂ = m; T₁ = T₂ = T ; a₁ = a₂ = a

F.cos 30₀ - T - k(mg - Fsin 30₀) = ma      (3)

T - kmg = ma                    (4)

Từ (3) và (4)

\[\Rightarrow T=\frac{T(cos{{30}^{\circ }}+\mu \sin {{30}^{\circ }})}{2}\le {{T}_{\max }}\]

\[F\le \frac{2{{T}_{\max }}}{cos{{30}^{\circ }}+\mu \sin {{30}^{\circ }}}=20\]

Vậy F_max = 20 N

Hướng dẫn

         

Khi thả vật A sẽ đi xuống và B sẽ đi lên do m_A > m_B và

T_A = T_B = T

a_A = a_B = a

Đối với vật A: m_Ag - T = m_A.a

Đối với vật B: -m_Bg + T = m_B.a

* (m_A - m_B).g = (m_A + m_B).a

\[a=\frac{{{m}_{A}}-{{m}_{B}}}{{{m}_{A}}+{{m}_{B}}}.g'=2m/{{s}^{2}}\]

Bài giải:

                    

Chọn chiều như hình vẽ. Ta có:

   \[\overrightarrow{{{P}_{3}}}+\overrightarrow{{{N}_{3}}}+\overrightarrow{{{F}_{3}}}+\overrightarrow{{{T}_{4}}}+\overrightarrow{{{T}_{3}}}+\overrightarrow{{{F}_{ms2}}}+\overrightarrow{{{P}_{2}}}+\overrightarrow{{{N}_{2}}}+\overrightarrow{{{T}_{2}}}+\overrightarrow{{{T}_{1}}}+\overrightarrow{{{P}_{1}}}=M\overrightarrow{a}\]  

Do vậy khi chiếu lên các hệ trục ta có:

\[\Rightarrow a=\frac{1-2\mu }{3}g=2m/{{s}^{2}}\]

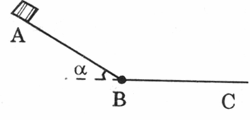
Hướng dẫn

         

Các lực tác dụng vào vật:

1. Trọng lực \[\overrightarrow{P}\]
2. Lực ma sát \[\overrightarrow{{{F}_{ms}}}\]
3. Phản lực \[\overrightarrow{N}\] của mặt phẳng nghiêng

4)       Hợp lực   

\[\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{ms}}}=m\overrightarrow{a}\]

Chiếu lên trục Oy: -Pcos\[\alpha \] + N = 0

 N = mg cos\[\alpha \]             (1)

Chiếu lên trục Ox : Psin\[\alpha \]- F_ms = max

mgsin\[\alpha \]- \[\mu \]N = max         (2)

từ (1) và (2) - mgsin\[\alpha \] - \[\mu \] mg cos\[\alpha \]= max

a = g(sin\[\alpha \]- \[\mu \]cos\[\alpha \])

          = 10(1/2 - 0,3464.\[\sqrt{3}\]/2) = 2 m/s₂

Hướng dẫn

         

Chọn hệ trục Oxy như hình vẽ.

Áp dụng định luật II Newtơn ta có :

\[\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{ms}}}=0\]

Chiếu phương trình lên trục Oy: N - Pcos\[\alpha \] - Fsin\[\alpha \] = 0

  N = Pcos\[\alpha \] + F sin\[\alpha \]

      F_ms = kN = k(mgcos\[\alpha \] + F sin\[\alpha \])

Chiếu phương trình lên trục Ox : Psin\[\alpha \] - F cos\[\alpha \] - F_ms = 0

 F cos\[\alpha \] = Psin\[\alpha \] - F_ms = mg sin\[\alpha \] - kmg cos\[\alpha \] - kF sin\[\alpha \]

\[\Rightarrow F=\frac{mg(\sin \alpha -k\cos \alpha )}{\cos \alpha +k\sin \alpha }=\frac{mg(tg\alpha -k)}{1+ktg\alpha }\]

Hướng dẫn

         

Giả thiết m₁ trượt xuống mặt phẳng nghiêng và m₂ đi lên, lúc đó hệ lực có chiều như hình vẽ. Vật chuyển động nhanh dần đều nên với chiều dương đã chọn, nếu ta tính được a > 0 thì chiều chuyển động đã giả thiết là đúng.

Đối với vật 1:         

\[\overrightarrow{{{T}_{1}}}+\overrightarrow{{{P}_{1}}}+\overrightarrow{N}+\overrightarrow{{{F}_{ms}}}={{m}_{1}}\overrightarrow{{{a}_{1}}}\]

Chiếu hệ xOy ta có: m₁gsin\[\alpha \] - T - \[\mu \]N = ma

                              -m₁g cos\[\alpha \] + N = 0

*    m₁gsin\[\alpha \] -T -\[\mu \]m₁g cos\[\alpha \] = ma          (1)

Đối với vật 2:

\[\overrightarrow{{{T}_{2}}}+\overrightarrow{{{P}_{2}}}={{m}_{2}}\overrightarrow{{{a}_{2}}}\]

Nên  -m₂g + T = m₂a                       (2)

Cộng (1) và (2) có m₁gsin\[\alpha \] -\[\mu \]m₁g cos\[\alpha \] = (m₁ + m₂)a

\[\Rightarrow a=\frac{mg\sin \alpha -\mu {{m}_{1}}\cos \alpha -{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}}\approx 0,6m/{{s}^{2}}\]

Vì a > 0, vậy chiều chuyển động đã chọn là đúng

* T = m₂ (g + a) = 1(10 + 0,6) = 10,6 N

 

 

Bài viết gợi ý: