Bài Tập Tổng Hợp Dao Động

BÀI TẬP TỔNG HỢP DAO ĐỘNG

Câu 1: Một vật có khối lượng 0,5 kg thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số góc 4π rad/s, \[{{x}_{1}}={{A}_{1}}\cos \left( \omega t+\frac{\pi }{6} \right)\]cm và \[{{x}_{2}}=4\sin \left( \omega t-\frac{\pi }{3} \right)\]cm. Biết hợp lực tác dụng lên vật có độ lớn cực đại là 2,4 N. Biên độ A₁ có giá trị:

A. 5 cm B. 6 cm C. 7 cm D. 3 cm

Hướng dẫn

Hợp lực cực đại tác dụng lên vật \[{{F}_{max}}=m{{\omega }^{2}}A\Leftrightarrow 2,4=0,5.{{\left( 4\pi \right)}^{2}}A\Rightarrow A=3cm\]

Ta có \[{{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \left( \Delta \varphi \right)\Leftrightarrow {{3}^{2}}=A_{1}^{2}+{{4}^{2}}+2.{{A}_{1}}.4\cos \left( \pi \right)\]\[\Rightarrow \]\[{{A}_{1}}=1cm\] hoặc \[{{A}_{1}}=7cm\]

Đáp án C

Câu 2: (Chuyên Vĩnh Phúc – 2017) Hai con lắc lò xo giống nhau gồm lò xo nhẹ và vật nặng có khối lượng 500 g, dao động điều hòa với phương trình lần lượt là \[{{x}_{1}}=Ac\text{os}\left( \omega t-\frac{\pi }{3} \right)\]cm và \[{{x}_{2}}=\frac{3A}{4}c\text{os}\left( \omega t+\frac{\pi }{6} \right)\]cm trên hai trục tọa độ song song cùng chiều, gần nhau và cùng gốc tọa độ. Biết trong quá trình dao động, khoảng cách giữa hai vật lớn nhất bằng 10 cm và vận tốc tương đối giữa chúng có độ lớn cực đại bằng 1 m/s. Để hai con lắc trên dừng lại phải thực hiện lên hệ hai con lắc một công cơ học có tổng độ lớn bằng

A. 0,25 J B. 0,1 J C. 0,5 J D. 0,15 J

Hướng dẫn

Khoảng cách lớn nhất giữa hai vật

\[d=\left| {{x}_{1}}-{{x}_{2}} \right|\Rightarrow {{d}_{ma\text{x}}}=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{\text{A}}_{1}}{{A}_{2}}\cos \Delta \varphi }=\frac{5\text{A}}{4}\]

Vận tốc tương đối giữa hai vật

\[v={{v}_{1}}-{{v}_{2}}\Rightarrow {{v}_{ma\text{x}}}=\sqrt{{{\left( \omega {{A}_{1}} \right)}^{2}}+{{\left( \omega {{A}_{2}} \right)}^{2}}-2\omega {{A}_{1}}\omega {{A}_{2}}\cos \Delta \varphi }=\frac{5\omega A}{4}\]

Từ hai phương trình trên \[\omega =10rad.{{s}^{-1}}\] và \[A=8cm\]

Để hai con lắc trên ngừng dao động ta phải cung cấp một công bằng tổng cơ năng của hai con lắc

\[A={{E}_{1}}+{{E}_{2}}=0,25\]J

Đáp án A

Câu 3: (Hoàng Lệ Kha – 2017) Một vật thực hiện đồng thời ba dao động cùng phương \[{{x}_{1}}={{A}_{1}}\cos \left( \omega t+\frac{2\pi }{3} \right)\]; \[{{x}_{2}}={{A}_{2}}\cos \left( \omega t \right)\], \[{{x}_{3}}={{A}_{3}}\cos \left( \omega t-\frac{2\pi }{3} \right)\]. Tại thời điểm t₁ các li độ có giá trị \[{{x}_{1}}=-10\]cm, \[{{x}_{2}}=40\]cm, \[{{x}_{3}}=-20\]cm. Tại thời điểm \[{{t}_{2}}={{t}_{1}}+\frac{T}{4}\] các giá trị li độ lần lượt là \[{{x}_{1}}=-10\sqrt{3}\]cm, \[{{x}_{2}}=0\]cm, \[{{x}_{3}}=20\sqrt{3}\]cm Tìm biên độ dao động tổng hợp

A. 50 cm B. 20 cm C. 30 cm D. \[40\sqrt{3}\]cm

Hướng dẫn

Hai thời điểm vuông pha \[A=\sqrt{x_{1}^{2}+x_{2}^{2}}\]

Ta tìm được \[{{A}_{1}}=20\]cm, \[{{A}_{2}}=40\]cm, \[{{A}_{3}}=40\]cm

\[\Rightarrow A=20\]cm

Đáp án B

Câu 4: (Hoàng Lệ Kha – 2017) Hai con lắc lò xo giống hệt nhau dao động điều hòa trên mặt phẳng nằm ngang dọc theo hai đường thẳng song song cạnh nhau và song song với trục Ox. Biên độ của con lắc thứ nhất là \[{{A}_{1}}=4\]cm, của con lắc thứ hai là \[{{A}_{2}}=4\sqrt{3}\]cm, con lắc thứ hai dao động sớm pha hơn con lắc thứ nhất. Trong quá trình dao động khoảng cách lớn nhất giữa hai vật dọc theo trục Ox là \[a=4\]cm. Khi động năng của con lắc thứ nhất cực đại là W thì động năng của con lắc thứ hai là

A. W B. \[\frac{3}{4}\text{W}\] C. \[\frac{9}{4}\text{W}\] D. \[\frac{2}{3}\text{W}\]

Hướng dẫn

Ta có:

\[{{d}_{ma\text{x}}}=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{\text{A}}_{1}}{{A}_{2}}\cos \Delta \varphi }=4\Rightarrow \Delta \varphi =\frac{\pi }{6}\]

Khi con lắc thứ nhất đi qua vị trí cân bằng thì con lắc thứ hai con li độ \[{{x}_{2}}=\frac{{{A}_{2}}}{2}\]

\[{{E}_{{{d}_{2}}}}=\frac{1}{2}k\text{A}_{2}^{2}-\frac{1}{2}k{{\left( \frac{{{A}_{2}}}{2} \right)}^{2}}=\frac{3}{4}\frac{1}{2}k\text{A}_{2}^{2}=\frac{9}{4}\text{W}\]

Đáp án C

Câu 5: (Yên Lạc – 2017) Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ \[{{A}_{1}}=6cm\] và trễ pha \[\frac{\pi }{2}\] so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ bằng 9 cm. Biên độ của dao động tổng hợp bằng

A. 18 cm B. 12 cm C. \[9\sqrt{3}\] cm D. \[6\sqrt{3}\] cm

Hướng dẫn

Khi \[x=9cm\]và \[{{x}_{2}}={{A}_{1}}=6cm\]\[\Rightarrow {{x}_{1}}=x-{{x}_{2}}=9-6=3cm\]

Vì \[{{x}_{1}}\bot x\Rightarrow \] khi \[{{x}_{1}}=3cm=\frac{{{A}_{1}}}{2}\] thì \[x=\frac{\sqrt{3}}{2}A\Rightarrow A=6\sqrt{3}cm\]

Đáp án D

Câu 6: (Chuyên Vinh – 2017) Hai dao động điều hòa có phương trình \[{{x}_{1}}=2\sin \left( 4t+{{\varphi }_{1}}+\frac{\pi }{2} \right)\] cm và \[{{x}_{2}}=2co\text{s}\left( 4t+{{\varphi }_{2}}+\frac{\pi }{2} \right)\]cm. Biết \[0\le {{\varphi }_{2}}-{{\varphi }_{1}}\le \pi \] và dao động tổng hợp có phương trình \[x=2\cos \left( 4t+\frac{\pi }{10} \right)\]cm. Giá trị của φ₁ là

A. \[-\frac{\pi }{18}\] B. \[-\frac{7\pi }{30}\] C. \[-\frac{\pi }{3}\] D. \[-\frac{42\pi }{90}\]

Hướng dẫn

Áp dụng kết quả tổng hợp dao động

Kết hợp với \[\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}\Leftrightarrow \tan \left( \frac{\pi }{18} \right)=\frac{\sin {{\varphi }_{1}}+\cos {{\varphi }_{2}}}{\cos {{\varphi }_{1}}-\sin {{\varphi }_{2}}}\]

+ Với \[{{\varphi }_{2}}={{\varphi }_{1}}+\frac{\pi }{6}\xrightarrow{SH\text{IFT+SOLVE}}{{\varphi }_{1}}=-\frac{7\pi }{30}\]

+ Với \[{{\varphi }_{2}}={{\varphi }_{1}}+\frac{5\pi }{6}\xrightarrow{SH\text{IFT+SOLVE}}{{\varphi }_{1}}=\frac{13\pi }{30}\]

Đáp án B

Câu 7: (Chuyên Long An – 2017) Hai điểm sáng dao động điều hòa trên trục Ox, chung vị trí cân bằng O, cùng tần số f, có biên độ dao động của điểm thứ nhất là A điểm thứ hai là 2A. Tại thời điểm ban đầu, điểm sáng thứ nhất đi qua vị trí cân bằng, điểm sáng thứ hai ở vị trí biên. Khoảng cách lớn nhất giữa hai điểm sáng là

A. \[\frac{A}{\sqrt{5}}\] B. \[A\sqrt{2}\] C. \[\frac{A}{\sqrt{2}}\] D. \[A\sqrt{5}\]

Hướng dẫn

Phương trình dao động của hai điểm sáng

Áp dụng kết quả tổng hợp dao động ta có

\[{{d}_{ma\text{x}}}=\sqrt{{{A}^{2}}+{{\left( 2\text{A} \right)}^{2}}+2.A.2\text{A}c\text{os}\Delta \varphi }\]

Trong mọi trường hợp ta luôn có \[\Delta \varphi =\left( 2k+1 \right)\frac{\pi }{2}\Rightarrow \cos \Delta \varphi =0\]

Vậy \[{{d}_{ma\text{x}}}=\sqrt{{{A}^{2}}+{{\left( 2\text{A} \right)}^{2}}}=\sqrt{5}\text{A}\]

Đáp án D

Câu 8: (Quốc Học – 2017) Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số có biên độ lần lượt là 8 cm và 12 cm. Biên độ dao động tổng hợp có thể là

A. 2 cm B. 3 cm C. 5 cm D. 21 cm

Hướng dẫn

Vậy \[{{A}_{\min }}\le A\le {{A}_{ma\text{x}}}\Leftrightarrow 12-8\le A\le 12+8\Leftrightarrow 4\le A\le 20\]

Đáp án C

Câu 9: (Quốc Học – 2017) Một vật nhỏ có chuyển động là tổng hợp của hai dao động điều hòa có phương trình \[{{x}_{1}}={{A}_{1}}\cos \left( \omega t \right)\]; \[{{x}_{2}}={{A}_{2}}\cos \left( \omega t+\frac{\pi }{2} \right)\]. Gọi W là cơ năng của vật. Khối lượng của vật nặng được tính theo công thức

A. \[m=\frac{2W}{{{\omega }^{2}}\left( A_{1}^{2}+A_{2}^{2} \right)}\] B. \[m=\frac{2W}{{{\omega }^{2}}\left( A_{1}^{2}-A_{2}^{2} \right)}\]

C. \[m=\frac{W}{{{\omega }^{2}}\left( A_{1}^{2}+A_{2}^{2} \right)}\] D. \[m=\frac{W}{{{\omega }^{2}}\left( A_{1}^{2}-A_{2}^{2} \right)}\]

Hướng dẫn

Hai dao động vuông pha \[\Rightarrow A=\sqrt{A_{1}^{2}+A_{2}^{2}}\]

Cơ năng của dao động \[\text{W}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Rightarrow m=\frac{\text{2W}}{{{\omega }^{2}}{{A}^{2}}}=\frac{\text{2W}}{{{\omega }^{2}}\left( A_{1}^{2}+A_{2}^{2} \right)}\]

Đáp án D

Câu 10: (Quốc Học – 2017) Một vật thực hiện đồng thời ba dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là \[{{x}_{1}}={{A}_{1}}\cos \left( 2\pi t+\frac{2\pi }{3} \right)\]cm, \[{{x}_{2}}={{A}_{2}}\cos \left( 2\pi t \right)\]cm, \[{{x}_{1}}={{A}_{3}}\cos \left( 2\pi t-\frac{2\pi }{3} \right)\]cm. Tại thời điểm t₁ các giá trị li độ là \[{{x}_{1}}=-20cm\], \[{{x}_{2}}=80cm\]; \[{{x}_{3}}=40\]cm, tại thời điểm \[{{t}_{2}}={{t}_{1}}+\frac{T}{4}\] các giá trị li độ \[{{x}_{1}}=-20\sqrt{3}cm\], \[{{x}_{2}}=0cm\]; \[{{x}_{3}}=40\sqrt{3}\]cm. Phương trình của dao động tổng hợp là

A. \[x=50\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm B. \[x=40\cos \left( 2\pi t-\frac{\pi }{3} \right)\]cm

C. \[x=40\cos \left( 2\pi t+\frac{\pi }{3} \right)\]cm D. \[x=20\cos \left( 2\pi t-\frac{\pi }{3} \right)\]cm

Hướng dẫn

Li độ tại hai thời điểm t₁ và t₂ vuông pha nhau nên ta có

Ghi chú:

Tổng hợp dao động bằng số phức:

+ Nhập dữ liệu: \[Mo\text{d}e\to 2\]

\[40\angle 120+80\angle 0+80\angle -120\]

+ Xuất kết quả: \[Shift\to 2\to 3\to =\]

\[40\angle -60\]

Vậy phương trình dao động tổng hợp là

\[x=40\cos \left( 2\pi t-\frac{\pi }{3} \right)\]cm

Đáp án B

Câu 11: (Chuyên KHTN – 2017) Một vật thực hiện đồng thời ba dao động điều hòa cùng phương, cùng tần số tương ứng là (1), (2), (3). Dao động (1) ngược pha và có năng lượng gấp đôi dao động (2). Dao động tổng hợp (13) có năng lượng là 3W. Dao động tổng hợp (23) có năng lượng W và vuông pha với dao động (1). Dao động tổng hợp của vật có năng lượng gần nhất với giá trị nào sau đây?

A. 2,7W B. 3,3W C. 2,3W D. 1,7W

Hướng dẫn

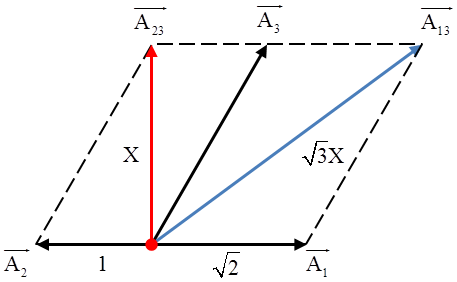
Phương pháp giản đồ vecto

\[{{E}_{1}}=2{{\text{E}}_{2}}\Rightarrow {{A}_{1}}=\sqrt{2}{{A}_{2}}\]

\[{{E}_{13}}=3{{\text{E}}_{23}}\Rightarrow {{A}_{13}}=\sqrt{3}\underbrace{{{A}_{23}}}_{X}\]

Chuẩn hóa \[{{A}_{2}}=1\Rightarrow {{A}_{1}}=\sqrt{2}\]

Từ hình vẽ ta có \[{{\left( \sqrt{3}X \right)}^{2}}={{X}^{2}}+{{\left( 1+\sqrt{2} \right)}^{2}}\Rightarrow X=\frac{1+\sqrt{2}}{\sqrt{2}}\]

Vì \[{{x}_{1}}\bot {{x}_{23}}\] nên biên độ của dao động tổng hợp của vật là

\[{{A}^{2}}=A_{23}^{2}+A_{1}^{2}={{\left( \frac{1+\sqrt{2}}{\sqrt{2}} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}\]

Ta có \[\frac{E}{{{E}_{23}}}=\frac{E}{\text{W}}=\frac{{{A}^{2}}}{A_{23}^{2}}=\frac{{{\left( \frac{1+\sqrt{2}}{\sqrt{2}} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}}{{{\left( \frac{1+\sqrt{2}}{\sqrt{2}} \right)}^{2}}}\approx 1,7\]

Đáp án D

Câu 12: (Chuyên KHTN – 2017) Hai chất điểm M và N có cùng khối lượng, dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của M và N đều nằm trên một đường thẳng đi qua gốc tọa độ và vuông góc với Ox. Biên độ của M là 6 cm, của N là 8 cm. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M có động năng bằng ba lần thế năng thì tỉ số giữa động năng của M và của N là

A. \[\frac{4}{3}\] B. \[\frac{9}{16}\] C. \[\frac{27}{16}\] D. \[\frac{3}{4}\]

Hướng dẫn

Khoảng cách giữa M và N trong quá trình dao động

\[d={{x}_{M}}-{{x}_{N}}=\sqrt{A_{M}^{2}+A_{N}^{2}-2{{\text{A}}_{M}}{{A}_{N}}\cos \Delta \varphi }\cos \left( \omega t+\phi \right)\]

Vậy \[{{d}_{\operatorname{m}ax}}=\sqrt{A_{M}^{2}+A_{N}^{2}-2{{\text{A}}_{M}}{{A}_{N}}\cos \Delta \varphi }=10\Rightarrow \Delta \varphi =\frac{\pi }{2}\]

Với hai đại lượng vuông pha ta luôn có

\[{{\left( \frac{{{x}_{M}}}{{{A}_{M}}} \right)}^{2}}+{{\left( \frac{{{x}_{N}}}{{{A}_{N}}} \right)}^{2}}=1,\]tại \[{{E}_{{{d}_{M}}}}={{E}_{{{t}_{M}}}}\Rightarrow {{x}_{M}}=\pm \frac{{{A}_{M}}}{2}\Rightarrow {{x}_{N}}=\pm \frac{\sqrt{3}}{2}{{A}_{N}}\]

Tỉ số động năng của M và N

\[\frac{{{E}_{{{d}_{M}}}}}{{{E}_{{{d}_{N}}}}}=\frac{{{E}_{M}}-{{E}_{{{t}_{M}}}}}{{{E}_{N}}-{{E}_{{{t}_{N}}}}}=\frac{A_{M}^{2}-{{\left( \frac{1}{2}A_{M}^{{}} \right)}^{2}}}{A_{N}^{2}-{{\left( \frac{\sqrt{3}}{2}A_{N}^{{}} \right)}^{2}}}=\frac{A_{M}^{2}}{A_{N}^{2}}\frac{\left( 1-\frac{1}{4} \right)}{\left( 1-\frac{3}{4} \right)}=\frac{27}{16}\]

Đáp án C

Câu 13: (Huỳnh Thúc Kháng – 2017) Một vật tham gia đồng thời hai dao động điều hòa kết hợp ngược pha nhau. Tại một thời điểm ly độ của dao động thành phần thứ nhất và dao động tổng hợp lần lượt là 2 cm và \[-3\] cm. Ở thời điểm ly độ dao động tổng hợp là 4,5 cm thì ly độ của dao động thành phần thứ hai là:

A. \[-3\] cm B. \[-7,5\] cm C. 7,5 cm D. 3 cm

Hướng dẫn

Tổng hợp dao động \[x={{x}_{1}}+{{x}_{2}}\xrightarrow[{{x}_{1}}=2]{x=-3}{{x}_{2}}=-5\Rightarrow \]dao động tổng hợp luôn cùng pha với dao động thứ hai

Biên độ của dao động thứ hai khi \[x=4,5\] là \[{{x}_{2}}=4,5\frac{-5}{-3}=7,5\]cm

Đáp án C

Câu 14: Hai chất điểm thực hiện dao động điều hòa trên hai đường thẳng song song, nằm ngang, có gốc tọa độ nằm cùng trên một đường thẳng có phương thẳng đứng. Phương trình dao động của các chất điểm tương ứng là \[{{x}_{1}}={{A}_{1}}\cos \left( \pi t+\frac{\pi }{6} \right)\]cm và \[{{x}_{2}}=6\cos \left( \pi t+\frac{\pi }{2} \right)\]cm (gốc thời gian là lúc hai vật bắt đầu chuyển động). Trong quá trình dao động, khoảng cách theo phương ngang giữa hai chất điểm được biểu diễn bằng phương trình \[d=Ac\text{os}\left( \omega t+\varphi \right)\]cm. Thay đổi A₁ đến khi biên độ A đạt giá trị cực tiểu thì

A. \[\varphi =-\frac{\pi }{6}\] B. \[\varphi =-\frac{\pi }{3}\] C. \[\varphi =0\] D. \[\varphi =\pi \]

Hướng dẫn

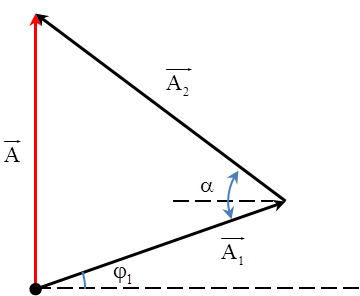
Khoảng cách giữa hai vật \[d=\left| {{x}_{1}}-{{x}_{2}} \right|\]

Từ hình vẽ ta có

\[\frac{A}{\sin \left( \frac{\pi }{2}-{{\varphi }_{1}} \right)}=\frac{{{A}_{2}}}{\sin \alpha }\Rightarrow A=\frac{{{A}_{2}}}{\sin \alpha }\sin \left( \frac{\pi }{2}-{{\varphi }_{1}} \right)\]

Để A_min thì \[\alpha =\frac{\pi }{2}\]\[\Rightarrow \varphi =-\frac{\pi }{3}\]