Chuyên đề : Dao động điều hòa
Các dạng bài toán trong dao động điều hòa
Bài toán liên quan đến quãng đường đi được lớn nhất , nhỏ nhất trong khoảng thời gian t
A) Lý thuyết cần nhớ
(*) trong dạng bài toán về quãng đường có một dạng biến tướng về quãng đường lớn nhất và nhỏ nhất , sau đây mình sẽ hướng dẫn các bạn giải quyết dạng toán này :
- ) Trong tất cả các chuyển động thì s luôn tỉ lệ thuận với vận tốc v
VD: +)Trong chuyển động thẳng đều ta có : $s=vt$ mà t là khoảng thời gian đang xét nên không đổi
+)Hay trong chuyển động nhanh dần đều thì : $s={{v}_{o}}t+\frac{1}{2}a{{t}^{2}}$ ( $a=\frac{v-{{v}_{o}}}{t-{{t}_{o}}}$ )
$\Rightarrow $ ${{S}_{\max }},{{S}_{\min }}$ sẽ phụ thuộc vào độ lớn của vận tốc
$\Rightarrow $ ${{S}_{\max }}$ khi ${{v}_{\max }}$ mà vận tốc lớn nhất khi vật đi qua VTCB
$\Rightarrow $Ngược lại : ${{S}_{\min }}$ khi ${{v}_{\min }}$ mà vận tốc nhỏ nhất khi vật đi qua vị trí biên.
1) Quãng đường lớn nhất .
$\leftrightarrow $ Như chúng ta tìm hiểu ở trên thì quãng đường lớn nhất là khi vật đi qua VTCB
(+) Giả sử trong khoảng thời gian $\Delta t$ vật đi từ M1 đến M2 ( được biểu diễn trên vòng tròn liên hệ như sau )
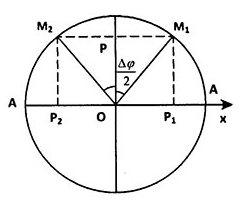
Quãng đường max chính là khoảng từ P1 đến P2
$\Rightarrow $ Ta có công thức tính quãng đường lớn nhất như sau :
$S=O{{P}_{1}}+O{{P}_{2}}=A.\sin \left( \frac{\Delta \varphi }{2} \right)+A.\sin \left( \frac{\Delta \varphi }{2} \right)=2A.\sin \left( \frac{\Delta \varphi }{2} \right)$
$\leftrightarrow $ Như chúng ta tìm hiểu ở trên thì quãng đường lớn nhất là khi vật đi qua VTCB
(+) Giả sử trong khoảng thời gian $\Delta t$ vật đi từ M1 đến M2 ( được biểu diễn trên vòng tròn liên hệ như sau )
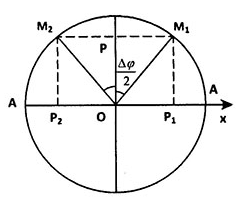
Quãng đường max chính là khoảng từ P1 đến P2
$\Rightarrow $ Ta có công thức tính quãng đường lớn nhất như sau :
$S=O{{P}_{1}}+O{{P}_{2}}=A.\sin \left( \frac{\Delta \varphi }{2} \right)+A.\sin \left( \frac{\Delta \varphi }{2} \right)=2A.\sin \left( \frac{\Delta \varphi }{2} \right)$
2) Quãng đường nhỏ nhất .
$\leftrightarrow $ Quãng đường nhỏ nhất là khi vật đi qua vị trí biên
(+) Giả sử trong khoảng thời gian $\Delta t$ vật đi từ M1 đến M2 ( được biểu diễn trên vòng tròn liên hệ như sau )
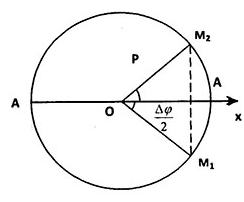
Quãng đường min là quãng đường đi từ M1 đến A rồi từ A về M2
$\Rightarrow $ Ta có công thức tính quãng đường nhỏ nhất như sau :
$S={{M}_{1}}\to A+A\to {{M}_{2}}=2A-(O{{M}_{1}}+O{{M}_{2}})$
$=2A-2.A.\cos \left( \frac{\Delta \varphi }{2} \right)=2A.\left( 1-\cos \left( \frac{\Delta \varphi }{2} \right) \right)$ .
Chú ý : Các khoảng thời gian đặc biệt T, T/2 quãng đường vật là không đổi lần lượt 4A , 2A nên trước khi làm chúng ta vẫn phải qua một bước là phân tích $\Delta t$ theo T .
$\leftrightarrow $ Quãng đường nhỏ nhất là khi vật đi qua vị trí biên
(+) Giả sử trong khoảng thời gian $\Delta t$ vật đi từ M1 đến M2 ( được biểu diễn trên vòng tròn liên hệ như sau )
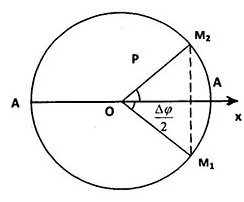
Quãng đường min là quãng đường đi từ M1 đến A rồi từ A về M2
$\Rightarrow $ Ta có công thức tính quãng đường nhỏ nhất như sau :
$S={{M}_{1}}\to A+A\to {{M}_{2}}=2A-(O{{M}_{1}}+O{{M}_{2}})$
$=2A-2.A.\cos \left( \frac{\Delta \varphi }{2} \right)=2A.\left( 1-\cos \left( \frac{\Delta \varphi }{2} \right) \right)$ .
Chú ý : Các khoảng thời gian đặc biệt T, T/2 quãng đường vật là không đổi lần lượt 4A , 2A nên trước khi làm chúng ta vẫn phải qua một bước là phân tích $\Delta t$ theo T .
3) Các bước thực hiện khi gặp dạng toán về quãng đường lớn nhất nhỏ nhất :
- B1 : Các bạn phải đọc kĩ đề , đổi đơn vị sao cho chuẩn ( tuy đơn giản nhưng rất nhiều bạn làm không cẩn thận )
- B2 : đọc đến phần tính quãng đường lớn nhất thì trong đầu phải nghĩ ngay ra công thức tính s max , quãng đường nhỏ nhất tương tự ( bản chất mình bài toán mình đã giải thích ở trên các bạn phải ghi nhớ công thức để làm nhanh)
- B3 : quan trọng nhất trong giải bài toán quãng đường lớn nhất nhỏ nhất là các bạn phải xác định góc quét theo công thức : $\Delta \varphi =\omega .\Delta t$
B) Một số dạng bài tập :
Câu 1 : Một vật dao động điều hòa với biên độ A , chu kì T . Quãng đường nhỏ nhất mà vật đi được trong khoảng thời gian T/6 là ???
A) $A(2-\sqrt{3})$
B) $A(1-\sqrt{3})$
C) $A(3-\sqrt{3})$
D) $A(4-\sqrt{3})$
Đáp án : A (*) sau khi đọc kĩ và xác định đề bài chúng ta sẽ đi tìm góc quét $\Delta \varphi $
Ta có : $\Delta \varphi =\omega .\Delta t=\frac{2\pi }{T}.\frac{T}{6}=\frac{\pi }{3}$
Áp dụng công thức Smin ta có : $S=2A.\left( 1-\cos \left( \frac{\Delta \varphi }{2} \right) \right)$ =$2A.\left( 1-\cos \left( \frac{\pi }{6} \right) \right)$ =$A(2-\sqrt{3})$ $\to A$
Câu 2 : Một vật dao động điều hòa với biên độ A , chu kì T . Quãng đường nhỏ nhất mà vật đi được trong khoảng thời gian 5T/6 là ???
A) 2A
B) 3A
C) 5A
D) $2\sqrt{3}A$
Đáp án : B (*) Đối với dạng toán có khoảng thời gian t lớn hơn T/2 ( khoảng thời gian đặc biệt ) thì chúng ta sẽ làm như mình chú ý ở trên như sau :
B1 : Phân tích $\Delta t$ theo T
Ta có : $\Delta t=\frac{5T}{6}=\frac{T}{2}+\frac{T}{3}={{S}_{{T}/{2}\;}}+{{S}_{\min {T}/{3}\;}}$ ( ${{S}_{{T}/{2}\;}}$=2A)
B2 : Tìm góc quét trong khoảng thời gian T/3
$\Delta \varphi =\omega .\Delta t=\frac{2\pi }{T}.\frac{T}{3}=\frac{2\pi }{3}$
B3 : Áp dụng công thức tìm quãng đường min :
\[{{S}_{\min }}=2A+2A.\left( 1-\cos \left( \frac{\Delta \varphi }{2} \right) \right)=2A+A=3A\] $\to B$
Câu 3 : Vật dao động điều hòa với phương trình x = 5cos(4πt + π/6) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian T/3
A) $5\sqrt{2}$
B) $5\sqrt{7}$
C) $5\sqrt{3}$
D) $5$
Đáp án : C (*) chúng ta khai thác \[\omega \] từ phương trình dao động,tìm góc quét, áp dụng công thức để giải quyết bài toán :
Ta có : ${{S}_{\max }}=2A.\sin \left( \frac{\Delta \varphi }{2} \right)$ ( $\Delta \varphi =\omega t=\frac{2\pi }{T}.\frac{T}{3}=\frac{2\pi }{3}$ ) = $5\sqrt{3}$ $\to C$
Câu 4 : Một chất điểm dao động điều hoà theo phương trình $x=5.\cos \left( 4\pi t \right)$. Trong khoảng thời gian 7/6 (s), quãng đường nhỏ nhất mà vật có thể đi được là ???
A) 28 cm
B) 40 cm
C) 35 cm
D) 45 cm
Đáp án : D (*) chúng ta vẫn làm bước quen thuộc là phân tích $\Delta t$ theo T
Ta có : $T=\frac{2\pi }{\omega }=\frac{2\pi }{4\pi }=0,5(s)$
Phân tích $\Delta t$ theo T ta sẽ lấy $\Delta t$ chia cho T rồi phân tích nhân chéo :
$\frac{\Delta t}{T}=\frac{7/6}{0,5}=2,33333$ = 2+0,3333 $\to $ $\Delta t$ = (2 + 0,33333).T =2T + $\frac{T}{3}$
Áp dụng công thức tính s min để hoàn thành bài toán :
${{S}_{\min }}={{S}_{2T}}+{{S}_{\min \left( {T}/{3}\; \right)}}=2.4A+{{S}_{\min \left( {T}/{3}\; \right)}}$
( với góc quét : $\Delta \varphi =\omega .\Delta t=\frac{2\pi }{T}.\frac{T}{3}=\frac{2\pi }{3}$ )|
$\to S=4.2A+A=45(cm)$ \[\to D\]
Câu 5 : Một vật dao động với chu kì T=2s , biên độ A = 5 cm . Tính quãng đường lớn nhất vật đi được trong 1/3 (s)
A) 5 cm
B) 10 cm
C) 15 cm
D) 20 cm

C) Bài tập tự luyện nâng cao khả năng
Câu 1 : Một vật dao động điều hòa với biên độ A , chu kì T . Quãng đường lớn nhất mà vật đi được trong khoảng thời gian T/4 là ???
A) $A\sqrt{2}$
B) $A\sqrt{3}$
C) A
D) 1,5 A
Câu 2 : Một vật dao động điều hòa với biên độ A , chu kì T . Quãng đường lớn nhất mà vật đi được trong khoảng thời gian 2T/3 là ???
A) 3A
B) 5A
C) 1,5 A
D) 2,5 A
Câu 3 : Một vật dao động điều hòa với phương trình : $x=4\cos \left( 2\pi t-\frac{\pi }{3} \right)$ . Quãng đường nhỏ nhất vật đi được trong khoảng thời gian 2/3chu kì là ???
A) 12
B) 10,26
C) 9,07
D) 10,92
Câu 4 : Một vật dao động điều hòa với phương trình : $x=5\cos \left( \pi t+\frac{\pi }{3} \right)$ .
Quãng đường lớn nhất vật đi được trong khoảng thời gian 1,5s là ???|
A) 28 cm
B) 20 cm
C) 10,92 cm
D) 17,07 cm
Câu 5: Một vật dao động điều hòa với phương trình : $x=5\cos \left( \pi t+\frac{\pi }{3} \right)$ .
Quãng đường nhỏ nhất vật đi được trong khoảng thời gian 1,5s là ???
A) 20cm
B) 7,07 cm
C) 17,07 cm
D) 13,66 cm
Câu 6 : Một vật dao động điều hòa với biên độ A , chu kì T . Quãng đường vật không thể đi C) Ađược trong khoảng thời gian T/3 là ???
A) $\sqrt{3}A$
B) 1,8 A
C) A
Gợi ý : Các bạn xét hết các phương diện nhỏ nhất , lớn nhất , …..
Câu 7 : Một vật dao động điều hòa với biên độ 4 cm . Quãng đường lớn nhất vật đi được trong 1s là 20m. Gia tốc lớn nhất của vật là ???
A) 3,49 $cm/{{s}^{2}}$
B) 244,82 $cm/{{s}^{2}}$
C) 284,44 $cm/{{s}^{2}}$
D) 4,64 $cm/{{s}^{2}}$
Câu 8 : Một vật dao động điều hòa với phương trình : $x=4\cos \left( 4\pi t+\frac{\pi }{3} \right)$ . Quãng đường nhỏ nhất vật đi được trong khoảng thời gian 1/6 s là
A) 2$\sqrt{3}$ cm
B) 3$\sqrt{3}$ cm
C) $\sqrt{3}$ cm
D) 4 cm
Câu 9 : Tìm quãng đường ngắn nhất vật đi từ vị trí có pha bằng $\frac{\pi }{6}$ đến vị trí lực phục hồi bằng một nửa cực đại là ??? Biết biên độ dao động là 3 cm
A) 1,09 cm
B) 0,45 cm
C) 1,5 cm
D) 1 cm
Câu 10 : Một vật dao động điều hòa tỉ lệ giữa quãng đường lớn nhất , nhỏ nhất trong T/4 là ???
A) 2$\sqrt{2}$
B) $\sqrt{2}$
C) $\sqrt{2}$ + 1
D) $\sqrt{2}$ + 2