I-
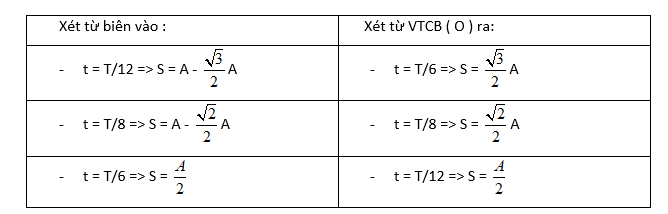
Một số điểm cần nhớ để thuận tiện trong quá trình giải
-
t
= T => S = 4A
-
t
= T/2 => S = 2A
- t = T/4 => S = A
II-
Dạng bài tính quãng đường trong giao động điều hòa
Dạng 1: Bài toán xác định quãng đường đi được
trong khoảng thời gian ∆t
Bước 1: Tính ∆φ;
∆φ
= ω. ∆t
Bước 2: Xoay thêm góc ∆φ kể từ vị trí t = 0 (s)
Bước 3: Tính quãng ñường bằng cách lấy
hình chiếu trên trục cos
Dạng 2: Bài toán xác định quãng đường vật đi được trong khoảng thời
gian từ t1 đến t2
Bước 1: Tìm ∆t ( ∆t = t2 –
t1 )
Bước 2: ∆t / T
ð ∆t = n.T + t3 => t2
= t1 + n.T + t3
Bước 3: Tìm S3;
S3 là quãng đường ứng với thời gian t3 kể từ t1
Bước 4: Tìm quãng
đường. S = n.4A + S3
III-
Ví dụ minh họa
Câu 1: Một vật giao động điều hòa
theo phương trình:
x = 1,25cos(2πt - π/12) (cm) (t đo bằng giây). Quãng đường vật
đi được trong khoảng thời gian t = 2,5s kể từ lúc bắt đầu dao động là:
|
A. 7,9 cm |
B. 22,5 cm |
C. 7,5 cm |
D.
12,5 cm |
Hưỡng dẫn
T = 2π / ω = 1
Theo đề có: t = 2,5 = T + T + $\frac{T}{2}$
ð S = 4A + 4A + 2A = 12,5
Câu 2: Cho dao động x = 6cos(5πt – π/4) cm). Tìm quãng đường vật đi được từ
thời điểm t1 = $\frac{7}{60}$s đến t2 = 6,73 s ?
|
A. 384 cm |
B. 397 cm |
C. 384,5 cm |
D.
397,5 cm |
Hướng dẫn
T = 2π / ω = 0,4
∆t / T = 248/15
=> ∆t = 16T + $\frac{8}{15}$T
Trong t3 = $\frac{8}{15}$T
:
Thay t1 vào x
=> x1 = 3
ð S3 =
3 + 6 + (6 – 1,875) = 13,15
ð S = 16.4.6 + 13,15 = 397,5
IV-
Bài tập tự luyện
Câu 1: Một vật nhỏ dao động điều hòa với biên độ A và chu kỳ
T. Quãng đường đi được trong nT là?
|
A. nA |
B. 2nA |
C. 3nA |
D.
4nA |
Hướng dẫn:
Ta có : t = T => s = 4A
Vậy t = nT => s = n4A
Câu 2: Một vật nhỏ dao động điều hòa có biên độ A, chu kỳ T, ở
thời điểm ban đầu t0 = 0 vật đang ở vị trí biên. Quãng đường vật đi
được từ thời điểm ban đầu đến thời điểm t = T/4 là?
|
A. A/2 |
B.
A |
C. 2A |
D. 4A |
Hướng dẫn:
Vật ở vị trí biên
Ta có: t = T/4 => s = A
Câu 3: Một vật giao động điều hòa với chu kì T và biên độ A. Ở
thời điểm ban đầu t0 = 0 vật đang ở vị trí biên, phát biểu nào sau
đây là sai?
|
A.
Sau T/8 vật đi được quãng đường A/2 |
B. Sau T/4 vật đi được quãng đường A |
|
C. Sau T/2 vật đi được quãng đường 2A |
D. Sau T vật đi được quãng đường 4A |
Hướng dẫn:
Vật ở vị trí biên
Ta có: t = T => s =
4A
t = T/2 => s = 2A
t = T/4
=> s = A
t = T/8
=> s = A - $\frac{\sqrt{2}}{2}$A
Câu 4: Một vật giao động điều hòa với phương trình x = 4cos(2πt + π/3) cm. Quãng đường mà vật đi được trong
thời gian 3s.
|
A.
48cm |
B. 15cm |
C. 56 cm |
D. 32cm |
Hướng dẫn:
T = 2π / ω = 1
Theo đề ta có t = 3 = 3T
ð S = 3.4A = 48 (cm)
Câu 5: Một vật nhỏ dao động điều hòa dọc theo trục Ox ( O là
vị trí cân bằng ) có phương trình dao động x = 7cos(2πt - π/3) cm (t tính bằng s). Tính quãng đường
mà vật đi được trong thời gian 5,5s.
|
A. 93 cm |
B. 105 cm |
C.
154 cm |
D. 140 cm |
Hướng dẫn:
T = 2π / ω = 1
Theo đề ta có: t = 5 = 5T + $\frac{1}{2}$T$$
ð S = 5.4A + 2A = 154 cm
Câu 6: Một vật giao động điều hòa theo phương trình x = 6cos(4πt + π/3) cm. Tính quãng đường vật đi được sau
t = 1(s) kể từ thời điểm ban đầu.
|
A. 24 cm |
B. 60 cm |
C. 64 cm |
D.
48 cm |
Hướng dẫn:
T = 2π / ω = 0,5
Theo đề ta có: t = 1 = 2T
ð s = 2.4A = 48 cm
Câu 7: Li độ của một vật giao động điều hòa có biểu thức x =
8cos(2πt – π) cm. Độ dài quãng đường mà vật đi được
trong khoảng thời gian ∆t
= 8/3 (s) tính từ thời điểm ban đầu là:
|
A.
84 |
B. 82 |
C. 80 |
D. $$80 + $2\sqrt{3}$ |
Hướng dẫn:
t0 = 0 => x0 = -8
T = 2π / ω = 1
Theo đề ta có t = 8/3 = 2T + $\frac{1}{2}$T + $\frac{1}{6}$T
ð S = 2.4A + 2A + $\frac{A}{2}$ = 64 + 16 + 4 =
84
Câu 8: Một vật giao động điều hòa với phương trình x = Acos(ω t + π/3) cm. Biết quãng đường vật đi được
trong thời gian 1s là 2A và trong $\frac{2}{3}$s đầu tiên là 9cm. Tính giá trị
của A và ω ?
|
A. 9 cm và π rad/s |
B. 12 cm và 2 π rad/s |
|
C.
6 cm và π
rad/s |
D. 12 cm và π rad/s |
Hướng dẫn:
Tại t0 = 0
=> x0 = A/2
Theo đề ta có: s = 2A => t = $\frac{T}{2}$ = 1 => T = 2
Mà T = 2π /
ω = 2 => ω = π
Theo đề ta có : t = $\frac{2}{3}$ = $\frac{T}{4}$ + $\frac{T}{12}$
ð S = A + $\frac{A}{2}$= 9 => A =6
Câu 9: Một vật giao động điều hòa với phương trình x = 5cos(4πt + π/3) cm. Xác định quãng đường vật đi được
sau t = $\frac{7T}{12}$ (s) kể từ thời điểm ban đầu?
|
A.
12
cm |
B.
10
cm |
C.
20
cm |
D. 12,5
cm |
Hướng
dẫn:
t0 = 0 => x0 = $\frac{5}{2}$
Theo đề ta có : t = $\frac{7T}{12}$ = $\frac{T}{2}$ + $\frac{T}{12}$
ð S = 2A + $\frac{A}{2}$= 10 + 2,5 =
12,5 cm
Câu 10: Một vật giao động điều hòa với phương trình x = Acos(6πt + π/3) cm. Sau khoảng thời gian ∆t = $\frac{7T}{12}$vật đi được quãng được s = 10 cm. Tìm biên độ
giao động của vật?
|
A. 5 cm |
B.
4 cm |
C. 3 cm |
D. 6 cm |
|
Hướng
dẫn:
t0 = 0 => x0 = $\frac{A}{2}$
Theo đề ta có : t = $\frac{7T}{12}$ = $\frac{T}{2}$ + $\frac{T}{12}$
ð S = 2A + $\frac{A}{2}$= 10 => A =
4
Câu 11: Một vật dao động điều hòa với phương trình x = 20cos(πt - 3π/4) cm. Quãng đường vật đi được từ thời
điểm t1 = 0,5s đến t2 =6s là:
|
A.
211,7 cm |
B. 201,2 cm |
C. 101,2 cm |
D. 202,2 cm |
Hướng dẫn:
T = 2π / ω = 2
|
|
Trong t3 = 0,75T = 0,5T + $\frac{T}{8}$ + $\frac{T}{8}$
Thay t1 = 0,5 vào x => x1 = $10\sqrt{2}$
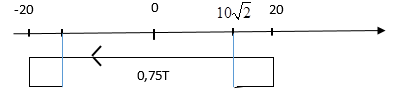
S3 = (20 - $10\sqrt{2}$) + 2A + (20 - $10\sqrt{2}$)
= 51,7 => S = 2.4A +51,7 = 211,7
Câu 12: Một vật dao động điều hòa với phương trình x = 8cos(2πt - 2π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 1s đến t2 = 29/6s là:
|
A. 124
cm |
B.
200
cm |
C.
152
cm |
D.
100
cm |
Hướng dẫn:
T = 2π / ω = 1
∆t / T = $\frac{23}{6}$$\frac{23}{6}$ => ∆t = 3T + $\frac{T}{2}$
+ $\frac{T}{3}$
Trong t3 = $\frac{T}{3}$ = $\frac{T}{12}$ + $\frac{T}{4}$
Thay t1 = 1 vào x => x1 = -4

ð S3 = A + 0,5A = 12 cm
ð S = 3.4A + 2A +12 = 124
Câu 13: Một vật dao động điều hòa với phương trình x = 5cos(8πt + π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 0 đến t2 =
1,5s là:
|
A.
20
cm |
B.
135
cm |
C.
15
cm |
D. 120
cm |
Hướng dẫn:
T = 2π / ω = ¼
∆t / T = 6 => ∆t = 6T
ð S = 4.6A = 120 cm.
Câu 14: Một vật dao động điều hòa với phương trình x = 6cos(4πt + π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 1,5 đến t2 =
3s là:
|
A.
38,42
cm |
B.
39,99
cm |
C.
39,8
cm |
D. Đáp
án khác |
Hướng dẫn:
T = 2π / ω = 0,5
∆t / T = 3 => ∆t = 3T
ð S = 3.4A = 72 cm.
Câu 15: Một vật dao động điều hòa với phương trình x = 3cos(4πt - π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 0 đến t2 = 2/3s là:
|
A. 15
cm |
B.
13,5
cm |
C.
21
cm |
D.
16,5
cm |
Hướng dẫn:
T = 2π / ω = 0,5
∆t / T = $\frac{4}{3}$ => ∆t = T + $\frac{T}{3}$
Trong t3 = $\frac{T}{3}$
= $\frac{T}{6}$ + $\frac{T}{6}$
Thay t1 = 0 vào x => x1 = 1,5
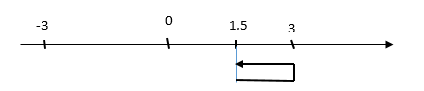
ð S3 = 1,5 + 1,5 = 3
ð S = 4A + 3 = 15
Câu 16: Một vật dao động điều hòa với phương trình x = 5cos(πt + 2π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 2 đến t2 = 19/3s là:
|
A. 42,5
cm |
B.
35
cm |
C.
22,5
cm |
D.
45
cm |
Hướng dẫn:
T = 2π / ω = 2
∆t / T = $\frac{13}{6}$ => ∆t = 2T + $\frac{T}{6}$
Trong t3 = $\frac{T}{6}$
Thay t1 = 2 vào x => x1 = -2,5
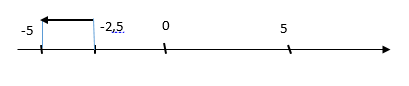
ð S3 = 2,5
ð S = 2.4A + 2,5 = 42,5
Câu 17: Một vật dao động điều hòa với phương trình x = 5cos(πt + 2π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 2 đến t2 = 17/3s là:
|
A.
25
cm |
B.
35 cm |
C.
30
cm |
D.
45
cm |
Hướng dẫn:
T = 2π / ω = 2
∆t / T = $\frac{11}{6}$ => ∆t = T + $\frac{T}{2}$ + $\frac{T}{3}$
Trong t3 = $\frac{T}{3}$
= $\frac{T}{6}$ + $\frac{T}{6}$
Thay t1 = 2 vào x => x1 = -2,5
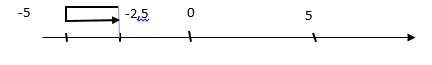
ð S3 = 2,5 + 2,5 = 5
ð S = 4A + 2A + 5 = 35
Câu 18: Một vật dao động điều hòa với phương trình x = 5cos(πt + 2π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 2 đến t2 = 29/6s là:
|
A.
25
cm |
B.
35
cm |
C. 27,5
cm |
D.
45
cm |
Hướng dẫn:
T = 2π / ω = 2
∆t / T = $\frac{17}{12}$ => ∆t = T + $\frac{5T}{12}$
Trong t3 = $\frac{5T}{12}$ = $\frac{T}{6}$+
$\frac{T}{4}$
Thay t1 = 2 vào x => x1 = -2,5

ð S3 = 2,5 + 2,5 + 2,5 = 7,5
ð S = 4A + 7,5 = 27,5
Câu 19: Một vật dao động điều hòa với phương trình x = 4cos(πt - π/2) cm. Quãng đường vật đi được từ thời
điểm t1 = 2 đến t2 = 4,25s là:
|
A.
16
+ $\sqrt{2}$cm |
B.
18
cm |
C. 16
+ $2\sqrt{2}$ cm |
D.
16
+ $2\sqrt{3}$ cm |
Hướng dẫn:
T = 2π / ω = 2
∆t / T = $\frac{9}{8}$ => ∆t = T + $\frac{T}{8}$
Trong t3 = $\frac{T}{8}$
Thay t1 = 2 vào x => x1 = 0
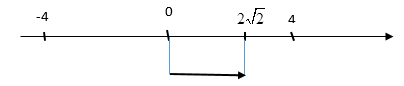
ð S3 = $2\sqrt{2}$
ð S = 4A + $2\sqrt{2}$ = 16 + $2\sqrt{2}$
Câu 20: Một vật dao động điều hòa dọc theo trục Ox với phương
trình x = 10cos(2πt + π/3) cm. Quãng đường vật đi được từ thời
điểm t1 = 0s đến t2 = 13/12 s là:
|
A.
15
cm |
B.
40
cm |
C. 45
cm |
D.
20
cm |
Hướng dẫn:
T = 2π / ω = 1
∆t / T = $\frac{13}{12}$ => ∆t = T + $\frac{T}{12}$
Trong t3 = $\frac{T}{12}$
Thay t1 = vào x => x1 = 5

ð S3 = 5
ð S = 4A + 5 = 45







