BÀI TOÁN ỨNG DỤNG THỰC TIỄN

Nhóm 1: Bài toán về quãng đường

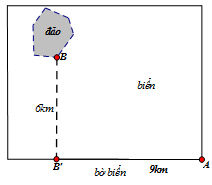
Câu 1. Một công ty muốn làm một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển 6km. Giá để xây đường ống trên bờ là 50.000USD mỗi km, và 130.000USD mỗi km để xây dưới nước. B’ là điểm trên bờ biển sao cho BB’ vuông góc với bờ biển. Khoảng cách từ A đến B’ là 9km. Vị trí C trên đoạn AB’ sao cho khi nối ống theo ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng:

A. 6.5km                                    B. 6km                              C. 0km                         D.9km

Hướng dẫn giải:

Đặt 

Chi phí xây dựng đường ống là 

Hàm C(x)  , xác định, liên tục trên [0,9]  và 

 

Vậy chi phí thấp nhất khi  x = 2,5 . Vậy C cần cách A một khoảng 6,5km.

Câu 2: Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển AB= 5km  .Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7 km  .Người canh hải đăng có thể chèo đò từ A đến M trên bờ biển với vận tốc 4 km/h  rồi đi bộ đến C với vận tốc 6km/h .Vị trí của điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?

Hướng dẫn giải:

 

Lập bảng biến thiên, ta thấy thời gian đến kho nhanh nhất khi 

Câu 3. Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra Côn Đảo (điểm C). biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A đến B là 100km, mỗi km dây điện dưới nước chi phí là 5000 USD, chi phí cho mỗi km dây điện trên bờ là 3000 USD. Hỏi điểm G cách A bao nhiêu để mắc dây điện từ A đến G rồi từ G đến C chi phí ít nhất.

 A: 40km                                     B: 45km                            C: 55km                       D:  60km

Hướng dẫn giải:

Gọi $BG=x(0

Ta có $GC=\sqrt{B{{C}^{2}}+G{{C}^{2}}}=\sqrt{{{x}^{2}}+3600}$

Chi phí mắc dây điện: $f(x)=3000.(100-x)+5000\sqrt{{{x}^{2}}+3600}$

Khảo sát hàm ta được: x = 45 . Chọn B.

Câu 4: Một màn ảnh chữ nhật cao 1,4 mét được đặt ở độ cao 1,8 mét so với tầm mắt (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn nhất. Hãy xác định vị trí đó ? ($\widehat{BOC}$ gọi là góc nhìn)

A. $AO=2,4m$                          B. $AO=2m$

C. $AO=2,6m$                           D. $AO=3m$

Hướng dẫn giải

Với bài toán này ta cần xác định OA để góc BOC lớn nhất.
Điều này xảy ra khi và chỉ khi tanBOC lớn nhất. Đặt OA = x (m) với x > 0,
ta có tanBOC = tan(AOC - AOB) = \[\frac{\tan AOC\,\,-\,\,\tan AOB}{1\,\,+\,\,\tan AOC.\tan AOB}\]

= \[\frac{\frac{AC}{OA}\,\,-\,\,\frac{AB}{OA}}{1\,\,+\,\,\frac{AC.AB}{O{{A}^{2}}}}\]   =  \[\frac{\frac{1,4}{x}}{1\,\,+\,\,\frac{3,2.1,8}{{{x}^{2}}}}\]  =  \[\frac{1,4x}{{{x}^{2}}+\,\,5,76}\]

Xét hàm số  f(x)  =  \[\frac{1,4x}{{{x}^{2}}+\,\,5,76}\]

Bài toán trở thành tìm x > 0 để f(x) đạt giá trị lớn nhất. Ta có

f'(x) =\[\frac{-1,4{{x}^{2}}+\,\,1,4.5,76}{{{({{x}^{2\,\,}}+\,\,5,76)}^{2}}}\],   f'(x) = 0 \[\Leftrightarrow \] x = \[\pm \]2,4

Ta có bảng biến thiên

Vậy vị trí đứng cho góc nhìn lớn nhất là cách màn ảnh 2,4m.

Câu 5:Từ cảng A dọc theo đường sắt AB cần phải xác định một trạm trung chuyển hàng hóa C và xây dựng một con đường từ C đến D. Biết rằng vận tốc trên đường sắt là v₁ và trên đường bộ là v₂ (v₁ < v₂). Hãy xác định phương án chọn địa điểm C để thời gian vận chuyển hàng từ cảng A đến cảng D là ngắn nhất?

Hướng dẫn giải:

Gọi t là thời gian vận chuyển hàng hóa từ cảng A đến cảng D.

 

Thời gian t là: t = \[\frac{AC}{{{v}_{1}}}\,\,+\,\,\frac{CD}{{{v}_{2}}}\] = \[\frac{AE\,-\,CE}{{{v}_{1}}}\,\,+\,\,\frac{CD}{{{v}_{2}}}\] = \[\frac{\ell \,-\,\frac{h}{\tan \alpha }}{{{v}_{1}}}\,\,+\,\,\frac{\frac{h}{\sin \alpha }}{{{v}_{2}}}\]   =  \[\frac{\ell \,\,-\,\,h.\cot \alpha }{{{v}_{1}}}\,\,-\,\,\frac{h}{{{v}_{2}}\,\sin \alpha }\]

Xét hàm số  \[t(\alpha )\,\,=\,\,\frac{\ell \,\,-\,\,h.\cot \alpha }{{{v}_{1}}}\,\,-\,\,\frac{h}{{{v}_{2}}\sin \alpha }\]. Ứng dụng Đạo hàm ta được \[t(\alpha )\] nhỏ nhất khi \[\cos \alpha \,\,=\,\,\frac{{{v}_{2}}}{{{v}_{1}}}\]. Vậy để t nhỏ nhất ta chọn C sao cho \[\cos \alpha \,\,=\,\,\frac{{{v}_{2}}}{{{v}_{1}}}\].

 Câu 6: Hai con tàu đang ở cùng một vĩ tuyến và cách nhau 5 hải lý. Đồng thời cả hai tàu cùng khởi hành, một chạy về hướng Nam với 6 hải lý/giờ, còn tàu kia chạy về vị trí hiện tại của tàu thứ nhất với vận tốc 7 hải lý/ giờ. Hãy xác định mà thời điểm mà khoảng cách của hai tàu là lớn nhất?

Hướng dẫn giải

Tại thời điểm t sau khi xuất phát, khoảng cách giữa hai tàu là d.

Ta có    d² = AB₁² + AA₁²   =  (5 - BB₁)² + AA₁²  = (5 - 7.t)² + (6t)²

Suy ra d = d(t)  = \[\sqrt{85{{t}^{2}}-\,\,70t\,\,+\,25}\].

Áp dụng Đạo hàm ta được d nhỏ nhất

khi \[t\,\,=\,\,\frac{7}{17}\](giờ), khi đó ta có d\[\approx \]3,25 Hải lý.

Nhóm 2: Bài toán diện tích hình phẳng

Câu 1: Cho hình chữ nhật có diện tích bằng $100(c{{m}^{2}})$. Hỏi mỗi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất?

A. $10cm\times 10cm$       B.  $20cm\times 5cm$   C.  $25cm\times 4cm$  D.  Đáp án khác

Hướng dẫn giải

Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là: $x(cm)$ và $y(cm)\,\,\,(x,y>0).$

Chu vi hình chữ nhật là: $P=2(x+y)=2x+2y$

Theo đề bài thì: $xy=100$ hay $y=\frac{100}{x}$. Do đó: $P=2(x+y)=2x+\frac{200}{x}$với $x>0$

Đạo hàm: $P'(x)=2-\frac{200}{{{x}^{2}}}=\frac{2{{x}^{2}}-200}{{{x}^{2}}}$. Cho \[y'=0\Leftrightarrow x=10\] .

Lập bảng biến thiên ta được: ${{P}_{\min }}=40$ khi $x=10\Rightarrow y=10$.

Kết luận: Kích thước của hình chữ nhật là $10\times 10$(là hình vuông).

Lưu ý: Có thể đánh giá bằng BĐT Cô-Sy: $P=2(x+y)\ge 2.2\sqrt{xy}=4\sqrt{100}=40.$

Câu 2 : Một lão nông chia đất cho con trai để người con canh tác riêng, biết người con sẽ được chọn miếng đất hình chữ nhật có chu vi bằng $800(m)$. Hỏi anh ta chọn mỗi kích thước của nó bằng bao nhiêu để diện tích canh tác lớn nhất?

A.$200m\times 200m$             B.$300m\times 100m$    C.$250m\times 150m$           D.Đáp án khác

Hướng dẫn giải

Gọi chiều dài và chiều rộng của miếng đất lần lượt là:  

Diện tích miếng đất: 

Theo đề bài thì:   . Do đó:

Đạo hàm:  

Lập bảng biến thiên ta được: 

Kết luận: Kích thước của miếng đất hình chữ nhật là 

 

Lưu ý: Có thể đánh giá bằng BĐT Cô-Sy.

Câu 3: Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là $180$ mét thẳng hàng rào. Ở đó người ta tận dụng một bờ giậu có sẵn để làm một cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Hỏi mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu?

A.${{S}_{max}}=3600{{m}^{2}}$    B.${{S}_{max}}=4000{{m}^{2}}$          C.${{S}_{max}}=8100{{m}^{2}}$                                 D.${{S}_{max}}=4050{{m}^{2}}$

Hướng dẫn giải

Gọi x là chiều dài cạnh song song với bờ giậu và y là chiều dài cạnh vuông góc với bờ giậu, theo bài ra ta có x+2y=180  . Diện tích của miếng đất là  S = y(180 – 2y).

Câu 4: Cần phải làm cái cửa sổ mà, phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là $a(m)$($a$  chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi độ dài cạnh hình chữ nhật là dây cung của hình bán nguyệt). Hãy xác định các kích thước của nó để diện tích cửa sổ là lớn nhất?

A. chiều rộng bằng\[\,\frac{2a}{4\,\,+\,\,\pi }\],  chiều cao bằng\[\,\frac{a}{4\,\,+\,\,\pi }\]

B.  chiều rộng bằng\[\,\frac{a}{4\,\,+\,\,\pi }\],  chiều cao bằng \[\,\frac{2a}{4\,\,+\,\,\pi }\]

C.  chiều rộng bằng\[\,a(4\,\,+\,\,\pi )\],  chiều cao bằng \[\,2a(4\,\,+\,\,\pi )\]

D.  Đáp án khác.

Hướng dẫn giải

Gọi $x$ là bán kính của hình bán nguyệt. Ta có chu vi của hình bán nguyệt là \[\pi \,x\], tổng ba cạnh của hình chữ nhật là $a-\pi x$. Diện tích cửa sổ là:

\[S\,\,=\,{{S}_{1}}+\,{{S}_{2}}\,=\,\,\frac{\pi \,{{x}^{2}}\,}{2}+\,2x\frac{a\,-\,\pi \,x\,-\,2x}{2}=ax-(\frac{\pi }{2}+2){{x}^{2}}=\,\,(\frac{\pi }{2}\,\,+\,\,2)x(\frac{a}{\frac{\pi }{2}\,\,+\,\,2}\,\,-\,\,x)\].

Dễ thấy $S$ lớn nhất khi \[x=\frac{a}{\frac{\pi }{2}\,\,+\,2\,}\,\,-\,\,x\] hay \[x\,\,=\,\,\frac{a}{4\,\,+\,\,\pi }\].(Có thể dùng đạo hàm hoặc đỉnh Parabol)

Vậy để $S{{\,}_{max}}$ thì các kích thước của nó là: chiều cao bằng\[\,\frac{a}{4\,\,+\,\,\pi }\]; chiều rộng bằng\[\,\frac{2a}{4\,\,+\,\,\pi }\]

Câu 5:Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số 120 cm từ tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này  là bao nhiêu?

Hướng dẫn giải

Kí hiệu cạnh góc vuông 

Khi đó cạnh huyền   , cạnh góc vuông kia là 

Diện tích tam giác ABC là:   . Ta tìm giá trị lớn nhất của hàm số này trên khoảng (0,60)

Ta có 

Lập bảng biến thiên ta có:

Tam giác ABC có diện tích lớn nhất khi BC=80  Từ đó chọn đáp án C.

Nhóm 3: Bài toán liên hệ diện tích, thể tích

 Câu 1: Có một tấm nhôm hình vuông cạnh 12 cm .Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x(cm) rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hình hộp nhận được có thể tích lớn nhất?

Câu 2: Một Bác nông dân cần xây dựng một hố ga không có nắp dạng hình hộp chữ nhật có thể tích  , tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng 2  . Hãy xác định diện tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất?

Hướng dẫn giải

 Câu 3: Người ta phải cưa một thân cây hình trụ có đường kính 1m , chiều dài 8m để được một cây xà hình khối chữ nhật như hình vẽ. Hỏi thể tích cực đại của khối gỗ sau khi cưa xong là bao nhiêu?

Hướng dẫn giải:

Câu 4: Bạn An là một học sinh lớp 12, bố bạn là một thợ hàn. Bố bạn định làm một chiếc thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:

Bằng kiến thức đã học em giúp bố bạn chọn mảnh tôn để làm được chiếc thùng có thể tích lớn nhất, khi đó chiều dài, rộng của mảnh tôn lần lượt là:

Hướng dẫn giải:

Câu 5: Một xưởng cơ khí nhận làm những chiếc thùng phi với thể tích theo yêu cầu là  lít mỗi chiếc. Hỏi bán kính đáy và chiều cao của thùng lần lượt bằng bao nhiêu để tiết kiệm vật liệu nhất?

Hướng dẫn giải:

Đổi   . Gọi bán kính đáy và chiều cao lần lượt là  

Ta có thể tích thùng phi    

Vật liệu tỉ lệ thuận với diện tích toàn phần nên ta chỉ cần tìm x để diện tích toàn phần bé nhất.

Nhóm 4: Bài toán lãi suất ngân hàng

Câu 1: Một người nọ đem gửi tiết kiệm ở một ngân hàng với lãi suất  là 12% năm. Biết rằng cứ sau mỗi  một quý ( 3 tháng ) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu bao nhiêu năm thì người đó nhận lại được số tiền, bao gồm cả vốn lẫn lãi gấp ba lần số tiền ban đầu.

A. 8                  B. 9                    C. 10                         D.11
 

Hướng dẫn giải

Gọi số tiền người đó gửi là A, lãi suất mỗi quý là 0,03

Sau n quý, tiền mà người đó nhận được là: 

Vậy số năm tối thiểu là xấp xỉ 9,29 năm. Vậy đáp án là C.

Câu 2: Ông Năm gửi $320$ triệu đồng ở hai ngân hàng X và Y theo phương thức lãi kép. Số tiền thứ nhất gửi ở ngân hàng X với lãi suất $2,1%$ một quý trong thời gian $15$ tháng. Số tiền còn lại gửi ở ngân hàng Y với lãi suất $0,73%$ một tháng trong thời gian $9$ tháng. Tổng lợi tức đạt được ở hai ngân hàng là $27\,507\,768,13$ (chưa làm tròn). Hỏi số tiền ông Năm lần lượt gửi ở ngân hàng X và Y là bao nhiêu?

A.$140$ triệu và $180$ triệu.                                             B.$180$ triệu và $140$ triệu.

C. $200$ triệu và $120$ triệu.                                            D. $120$ triệu và $200$ triệu.

Hướng dẫn giải:

Câu 3: Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng (chuyển vào tại khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi suất 1% trên một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ số tiền (gồm số tiền của tháng 12 và số tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (Kết quả làm tròn theo đơn vị nghìn đồng).

A. 50 triệu 730 nghìn đồng     B.  48 triệu 480 nghìn đồng

C. 53 triệu 760 nghìn đồng     D. 50 triệu 640 nghìn đồng

Hướng dẫn giải

Số tiền tháng 1 mẹ được nhận là 4 triệu, gửi đến đầu tháng 12 (được 11 kỳ hạn), vậy cả vốn lẫn lãi do số tiền tháng 1 nhận sinh ra là:  (triệu đồng).

Tương tự số tiền tháng 2 nhận sẽ sinh ra:  (triệu đồng)

............................

Số tiền tháng 12 mẹ lĩnh luôn nên là: 4 (triệu đồng).

Vậy tổng số tiền mẹ lĩnh là:   (50 triệu 730 nghìn đồng). Đáp án A.

Câu 4: Một Bác nông dân vừa bán một con trâu được số tiền là 20.000.000 (đồng) .Do chưa cần dùng đến số tiền nên Bác nông dân mang toàn bộ số tiền đó đi gửi tiết kiệm loại kỳ hạn 6 tháng vào ngân hàng với lãi suất 8.5% một năm thì sau 5 năm 8 tháng Bác nông dân nhận được bao nhiêu tiền cả vốn lẫn lãi .Biết rằng Bác nông dân đó không rút cả vốn lẫn lãi tất cả các định kì trước và nếu rút trước thời hạn thì ngân hàng trả lãi suất theo loại không kì hạn 0.01% một ngày (1 tháng tính 30 ngày)

Hướng dẫn giải

Một kì hạn 6 tháng có lãi suất là  . Sau 5 năm 6 tháng (có nghĩa là 66 tháng tức là 11 kỳ hạn) , số tiền cả vốn lẫn lãi Bác nôn dân nhận được là :  .Vì 5 năm 8 tháng thì có 11 kỳ hạn và dư 2 tháng hay dư 60 ngày nên số tiền A được tính lãi suất không kỳ hạn trong 60 ngày là :

 

 Suy ra sau 5 năm 8 tháng số tiền bác nông dân nhận được là

 

Nhóm 5: Bài toán liên quan đến mũ, loga

Câu 1. Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu²³⁹ là 24360 năm (tức là một lượng Pu²³⁹ sau 24360 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức S = Ae^rt, trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hàng năm (r<0), t là thời gian phân hủy, S là lượng còn lại sau thời gian phân hủy t. Hỏi sau bao nhiêu năm thì 10 gam Pu²³⁹ sẽ phân hủy còn 1 gam có giá trị gần nhất với giá trị nào sau?

A. 82135                                     B. 82335                            C. 82235                       D. 82435

Hướng dẫn giải:

Câu 1. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức:  , trong đó  là khối lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cabon  là khoảng 5730 năm. Cho trước mẫu Cabon có khối lượng 100g. Hỏi sau khoảng thời gian t thì khối lượng còn bao nhiêu?

Hướng dẫn giải:

Câu 2. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức:  , trong đó  là khối lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cabon  là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng Cabon và xác định được nó đã mất khoảng 25% lượng Cabon ban đầu của nó. Hỏi mẫu đồ cổ đó có tuổi là bao nhiêu?

A.2378 năm                               B. 2300 năm                     C. 2387 năm                D. 2400 năm

Hướng dẫn giải:

Câu 3. Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức quảng cáo trên truyền hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau x quảng cáo được phát thì số % người xem mua sản phẩm là  . Hãy tính số quảng cáo được phát tối thiểu để số người mua đạt hơn 75%.

A. 333                              B. 343                           C. 330                           D. 323

Hướng dẫn giải

Khi có 100 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm là:

Khi có 200 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm là:

Khi có 500 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm là:

Đáp án: A.

Câu 4. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức  , trong đó .A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng (r >0 ) , x (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần

Hướng dẫn giải

thời gian cần tìm là t. Ta có: 5000 = 1000. e^10r nên   .

Do đó, 10000 = 1000. e^rt suy ra t =    nên chọn câu C.

Nhóm 6: Bài toán ứng dụng tích phân, mối quan hệ đạo hàm-nguyên hàm

Câu 1: Một vật di chuyển với gia tốc  . Khi  t=0 thì vận tốc của vật là 30m/s . Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).

Hướng dẫn giải:

Câu 2. Một ô tô chạy với vận tốc 20m/s thì người lái xe đạp phanh còn được gọi là “thắng”. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc\[v\left( t \right)=-40t+20\,\,\,\left( m/s \right)\]  Trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh . Quãng đường ô tô di chuyển từ lúc đạp phanh đến khi dừng hẳn là bao nhiêu?

A. 2m                                          B.3m                                  C.4m                             D. 5m

Hướng dẫn giải

Lấy mốc thời gian là lúc ô tô bắt đầu phanh (t = 0)

Gọi T là thời điểm ô tô dừng lại. Khi đó vận tốc lúc dừng là v(T) = 0

Vậy thời gian từ lúc đạp phanh đến lúc dừng là 

Gọi s(t) là quãng đường ô tô đi được trong khoảng thời gian T.

Ta có   suy ra s(t) là nguyên hàm của v(t)

Vây trong ½ (s) ô tô đi được quãng đường là 

Câu 3. Một tấm bìa cứng hình chữ nhật có kích thước 3m x 8m . Người ta cắt mỗi góc của tấm bìa một hình vuông có cạnh là x để tạo ra hình hộp chữ nhật không nắp. Với giá trị nào của x thì thể tích hình hộp chữ nhật đạt giá trị lớn nhất ?

Hướng dẫn giải:

 

Chọn đáp án C

Câu 4.Một người vay 100 triệu đồng, trả góp theo tháng trong vòng 36 tháng, lãi suất là \[0,75%\]/ tháng. Số tiền người đó phải trả hàng tháng (trả tiền vào cuối tháng, số tiền làm tròn đến hàng nghìn) là:

* Chọn đáp án A

 

 

 

Bài viết gợi ý: