BÀI TOÁN VỀ BIẾN
THIÊN CHU KÌ CON LẮC
(SỰ NHANH CHẬM ĐỒNG
HỒ QUẢ LẮC)
I.
CHU KÌ THAY ĐỔI LỚN
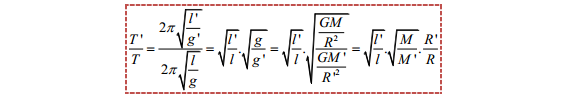
Ví
dụ 1: Một con lắc đơn
khi dao động trên mặt đất, chu kì dao động 2 s. Dem con lắc lên Mặt Trăng mà
không thay đổi chiều dài thì chu kì dao động của nó là bao nhiêu. Biết rằng khối
lượng Trái Đất gấp 81 lần khối lượng Mặt Trăng, bán kính Trái Đất bằng 3,7 lần
bán kính Mặt Trăng.
A. 4,865 s B. 4,566 s C. 4,685 s D. 4,658
Hướng dẫn:
$\frac{T'}{T}=\sqrt{\frac{M}{M'}}.\frac{R'}{R}=\sqrt{81}.\frac{1}{3,7}\xrightarrow{T=2s}T'\simeq
4,865s$ $\to $ Chọn A
Ví
dụ 2: Một
con lắc đơn khi dao động trên mặt đất tại nơi có gia tốc trọng trường 9,819 $m/{{s}^{2}}$
chu kì dao động 2 s. Đưa con lắc đơn đến nơi khác có gia tốc trọng trường 9,793
$m/{{s}^{2}}$mà không thay đổi chiều dài thì chu kì dao động là:
A. 2,002 s B. 2,003 s C. 2,004 s D. 2,005 s
Hướng dẫn:
$\frac{T'}{T}=\sqrt{\frac{g}{g'}}\to \frac{T'}{2}=\sqrt{\frac{9,819}{9,793}}\to T'\approx 2,003$ (s) $\to $ Chọn B
II.
CHU KÌ THAY ĐỔI NHỎ (sự nhanh chậm đồng hồ quả lắc)
Đồng
hồ chạy đúng có chu kì ${{\text{T}}_{\text{0}}}$ với chiều dài dây treo là ${{\text{l}}_{\text{0}}}$,
gia tốc ${{\text{g}}_{\text{0}}}$ trên mặt đất ở nhiệt độ ${{\text{t}}_{\text{0}}}$.
Đồng
hồ chạy sai có chu kì T với chiều dài dây treo là l, gia tốc rơi tự do g, ở độ
cao (hoặc độ sâu) ${{\text{h}}_{\text{c}}}$ (hoặc ${{\text{h}}_{\text{s}}}$) ở
nhiệt độ t.
Trong
khoảng thời gian t, đồng hồ chạy sai chỉ thời gian: $\frac{t}{T}.{{T}_{0}}$
Đồng
hồ chạy sai: $\Delta t=\frac{t}{T}.{{T}_{0}}-t=t.\frac{{{T}_{0}}-T}{T}=t.\frac{\Delta
T}{T}$
**
$\Delta t>0$: đồng hồ chạy nhanh
$\Delta t>0$: đồng hồ chạy chậm
Công thức gần đúng: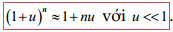
1.
Biến thiên chu kì do thay đổi nhiệt độ:
Chiều
dài dây treo ở nhiệt độ t: $\text{l =
}{{\text{l}}_{{{\text{0}}^{\text{0}}}\text{C}}}\text{(1+ }\!\!\alpha\!\!\text{
t)}$; ${{\text{l}}_{{{\text{0}}^{\text{0}}}\text{C}}}$ là chiều dài con lắc ở
nhiệt độ ${{\text{0}}^{\text{0}}}\text{C}$, $\text{ }\!\!\alpha\!\!\text{ }$ là
hệ số nở dài dây treo.
${{T}_{0}}=2\pi
\sqrt{\frac{{{l}_{0}}}{{{g}_{0}}}}=2\pi \sqrt{\frac{{{l}_{{{0}^{0}}C}}(1+\alpha
{{t}_{0}})}{{{g}_{0}}}}$ ; $T=2\pi \sqrt{\frac{l}{{{g}_{0}}}}=2\pi
\sqrt{\frac{{{l}_{{{0}^{0}}C}}(1+\alpha t)}{{{g}_{0}}}}$
\[\to
\frac{{{T}_{0}}}{T}=\frac{{{\left( 1+\alpha {{t}_{0}} \right)}^{\frac{1}{2}}}}{{{(1+\alpha
t)}^{\frac{1}{2}}}}\simeq \left( 1+\frac{1}{2}\alpha {{t}_{0}} \right)\left(
1-\frac{1}{2}\alpha t \right)=1-\frac{\alpha }{2}(t-{{t}_{0}})-\frac{{{\alpha
}^{2}}}{4}.t.{{t}_{0}}\approx 1-\frac{\alpha }{2}(t-{{t}_{0}})\]
$\to
\frac{\Delta T}{T}=\frac{{{T}_{0}}-T}{T}=-\frac{\alpha \Delta t}{2}$
Thời
gian đồng hồ chạy sai trong khoảng thời gian t là $\Delta t=t.\frac{\Delta
T}{T}=t.\left( -\frac{\alpha \Delta t}{2} \right)$
2.
Biến thiên chu kì do cắt (nối) một đoạn rất nhỏ ($\Delta l$):
$l={{l}_{0}}+\Delta l$
*
$\Delta l<0$: cắt bớt
$\Delta l>0$ : nối thêm
${{T}_{0}}=2\pi
\sqrt{\frac{{{l}_{0}}}{{{g}_{0}}}}$, $T=2\pi \sqrt{\frac{l}{{{g}_{0}}}}=2\pi
\sqrt{\frac{{{l}_{0}}+\Delta l}{{{g}_{0}}}}$
$\to
\frac{{{T}_{0}}}{T}=\sqrt{\frac{{{l}_{0}}}{{{l}_{0}}+\Delta
l}}=\sqrt{\frac{1}{1+\frac{\Delta l}{{{l}_{0}}}}}={{\left( 1+\frac{\Delta
l}{{{l}_{0}}} \right)}^{\frac{-1}{2}}}\simeq 1-\frac{\Delta l}{2{{l}_{0}}}$
$\to
\frac{\Delta T}{T}=\frac{{{T}_{0}}-T}{T}=-\frac{\Delta l}{2{{l}_{0}}}$
Thời
gian đồng hồ chạy sai trong khoảng thời gian t là $\Delta t=t.\frac{\Delta
T}{T}=t.\left( -\frac{\Delta l}{2{{l}_{0}}} \right)$
3.
Biến thiên chu kì do thay đổi vĩ độ: $g={{g}_{0}}+\Delta g$
${{T}_{0}}=2\pi
\sqrt{\frac{{{l}_{0}}}{{{g}_{0}}}}$, $T=2\pi \sqrt{\frac{l}{{{g}_{0}}}}=2\pi
\sqrt{\frac{l}{{{g}_{0}}+\Delta g}}$
$\to
\frac{{{T}_{0}}}{T}=\sqrt{\frac{{{g}_{0}}+\Delta
g}{{{g}_{0}}}}=\sqrt{1+\frac{\Delta g}{{{g}_{0}}}}\simeq 1+\frac{\Delta
g}{2{{g}_{0}}}$
$\to
\frac{\Delta T}{T}=\frac{{{T}_{0}}-T}{T}=\frac{\Delta g}{2{{g}_{0}}}$
Thời
gian đồng hồ chạy sai trong khoảng thời gian t là $\Delta t=t.\frac{\Delta
T}{T}=t.\left( \frac{\Delta g}{2{{g}_{0}}} \right)$
4.
Biến thiên chu kì do thay đổi độ cao:
${{T}_{0}}=2\pi
\sqrt{\frac{{{l}_{0}}}{{{g}_{0}}}}=2\pi \sqrt{\frac{{{l}_{0}}{{R}^{2}}}{GM}}$, $T=2\pi
\sqrt{\frac{{{l}_{0}}}{g}}=2\pi \sqrt{\frac{{{l}_{0}}{{\left( R+{{h}_{c}}
\right)}^{2}}}{GM}}$
$\to
\frac{{{T}_{0}}}{T}=\frac{R}{R+{{h}_{c}}}=\frac{1}{1+\frac{{{h}_{c}}}{R}}={{\left(
1+\frac{{{h}_{c}}}{R} \right)}^{-1}}=1-\frac{{{h}_{c}}}{R}$
$\to
\frac{\Delta T}{T}=\frac{{{T}_{0}}-T}{T}=-\frac{{{h}_{c}}}{R}$
Thời
gian đồng hồ chạy sai trong khoảng thời gian t là $\Delta t=t.\frac{\Delta
T}{T}=t.\left( -\frac{{{h}_{c}}}{R} \right)$
${{g}_{0}}=\frac{GM}{{{R}^{2}}}=\frac{G.\frac{4}{3}\pi
{{R}^{3}}.D}{{{R}^{2}}}=\frac{4}{3}\pi .G.D.R$ (D là khối lượng riêng Trái Đất)
$g=\frac{GM'}{{{\left(
R-{{h}_{s}} \right)}^{2}}}=\frac{G.\frac{4}{3}\pi .{{\left( R-{{h}_{s}}
\right)}^{3}}.D}{{{\left( R-{{h}_{s}} \right)}^{2}}}=\frac{4}{3}\pi .G.D.\left(
R-{{h}_{s}} \right)$
\[\to
\frac{{{T}_{0}}}{T}=\sqrt{\frac{R-{{h}_{s}}}{R}}=\frac{1}{\sqrt{\frac{R-{{h}_{s}}+{{h}_{s}}}{R-{{h}_{s}}}}}={{\left(
1+\frac{{{h}_{s}}}{R-{{h}_{s}}} \right)}^{\frac{-1}{2}}}\simeq
1-\frac{{{h}_{s}}}{2\left( R-{{h}_{s}} \right)}\simeq 1-\frac{{{h}_{s}}}{2R}\]
$\to
\frac{\Delta T}{T}=\frac{{{T}_{0}}-T}{T}=-\frac{{{h}_{s}}}{2R}$
Thời
gian đồng hồ chạy sai trong khoảng thời gian t là $\Delta t=t.\frac{\Delta
T}{T}=t.\left( -\frac{{{h}_{s}}}{2R} \right)$
6.
Biến thiên chu kì do lực Acsimet:
$\frac{{{T}_{0}}}{T}=\sqrt{\frac{g}{{{g}_{0}}}}=\sqrt{\frac{{{g}_{0}}-\frac{d{{g}_{0}}}{D}}{{{g}_{0}}}}={{\left(
1-\frac{d}{D} \right)}^{\frac{1}{2}}}=1-\frac{d}{2D}$
$\to
\frac{\Delta T}{T}=\frac{{{T}_{0}}-T}{T}=-\frac{d}{2D}$
Thời gian đồng hồ chạy sai trong khoảng thời gian t là $\Delta t=t.\frac{\Delta T}{T}=t.\left( -\frac{d}{2D} \right)$
Tổng
quát: Thời gian đồng hồ chạy sai trong khoảng thời gian
t là:
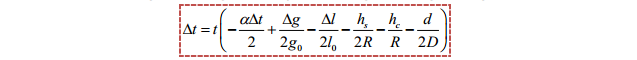
Ví dụ minh họa:
Ví dụ 1: Một con lắc đơn dao động nhỏ với chu kì 4,002 (s). Nếu
tăng chiều dài 0,2% và giảm gia tốc trọng trường 0,3% thì chu kì dao động bằng:
A. 4,010 B. 4, 009 C.
4,012 D.
4,014
Hướng dẫn:
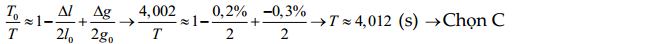
Ví dụ 2: Một con lắc đơn với quả cầu làm bằng chất có khối lượng
riêng D, dao động điều hòa trong chân không. Nếu đưa ra không khí (không khí có
khối lượng riêng d = D/500) thì chu kì dao động điều hòa tăng hay giảm bao
nhiêu phần trăm? Bỏ qua mọi ma sát.
A.
giảm 0,1% B. giảm 0,05% C. tăng 0,05% D. tăng 0,1%
Hướng dẫn:
Ví dụ 3: Ở ${{23}^{0}}C$ tại mặt đất, một con lắc dao động điều
hòa với chu kì T. Khi đưa con lắc lên cao 448 m thì chu kì vẫn là T. Biết hệ số
nở dài của thanh treo con lắc là ${{2.10}^{-5}}$ (1/K), bán kính Trái Đất là
6400 km.Nhiệt độ ở độ cao này là:
A. ${{10}^{0}}C$ B.
${{12}^{0}}C$ C. ${{14}^{0}}C$ D.
${{16}^{0}}C$
Hướng dẫn:
$\Delta
T=-\frac{1}{2}\alpha (t-{{t}_{0}})-\frac{h}{R}=0\to
-\frac{1}{2}{{.2.10}^{-5}}(t-23)-\frac{448}{{{6400.10}^{3}}}=0\to
t={{16}^{0}}C\to $ Chọn D
Ví
dụ 4: Người ta đưa một đồng hồ quả lắc chạy đúng ở mặt
đất lên độ cao h = 0,5 km, nhiệt độ không đổi. Biết bán kính Trái Đất là 6400
km. Mỗi ngày đêm đồng hồ nhanh chậm:
A.
Nhanh 6,75 s B. Chậm
6,75 s C. Nhanh
6,5 s D. Chậm
6,5 s
Hướng dẫn:
t = 1 ngày = 24.3600 (s)
$\Delta t=t.\frac{\Delta T}{T}=t.\left( -\frac{h}{R} \right)=24.3600.\left( -\frac{0,5}{6400} \right)=-6,75$ (s) $\to $ Chọn B
Ví
dụ 5: Đồng hồ quả lắc chạy đúng ở Hà Nội với chu kì 2
s, ${{g}_{1}}$ = 9,7926 $m/{{s}^{2}}$ và nhiệt độ ${{t}_{1}}={{10}^{0}}C$. Khi
chuyển đồng hồ vào Sài Gòn có ${{g}_{2}}$ = 9,7867 $m/{{s}^{2}}$ và nhiệt độ ${{t}_{2}}={{33}^{0}}C$.
Biết hệ số nở dài của thanh treo con lắc là ${{2.10}^{-5}}$ (1/K). Muốn đồng hồ
chạy đúng thì tăng, giảm chiều dài dây treo như thế nào?
A.
Giảm 1,05 cm B. Tăng 1,05
cm C. Giảm 1,05 mm D. Tăng 1,05 mm
Hướng dẫn:
$\Delta
T=0\to -\frac{\Delta
l}{2{{l}_{1}}}+\frac{{{g}_{2}}-{{g}_{1}}}{2{{g}_{1}}}-\frac{\alpha \left(
{{t}_{2}}-{{t}_{1}} \right)}{2}=0$
$\xrightarrow{{{l}_{1}}={{g}_{1}}.{{\left(
\frac{T}{2\pi } \right)}^{2}}=0,9922}\Delta l=-0,00105$(m) = -1,05 (mm)$\to $
Chọn C
Ví
dụ 6: Cho một con lắcđơn treo ở đầu một sợi dây mảnh
dài bằng kim loại, vặt nặng làm bằng chất có khối lượng riêng D = 8 $g/c{{m}^{3}}$.
Khi dao động nhỏ trong bình chân không đặt trên mặt đất thì chu kì dao động là
T. Cho con lắc đơn dao động trong bình chứa một chất khí có khối lượng riêng
0,002 ($g/c{{m}^{3}}$), đồng thời đưa bình lên độ cao h so với mặt đất. Ở trên
đó nhiệt độ thấp hơn so với mặt đất là ${{20}^{0}}C$ thì thấy chu kì dao động vẫn
là T.Biết hệ số nở dài của dây treo là 2,32.${{10}^{-5}}$ (1/K). Coi Trái Đất
hình cầu, bán kính là 6400 km. Xác định h.
A.
0,68 km B. 0,78
km C. 0,88 km D. 0,98 km
Hướng dẫn:
$\Delta
T=0\to -\frac{h}{R}-\frac{\alpha \Delta t}{2}-\frac{d}{2D}=0$
$\to
-\frac{h}{6400}-\frac{2,{{32.10}^{-5}}\left( -20
\right)}{2}-\frac{0,002}{2.8}=0\to h=0,6848$ (km)
Bài
tập tự luyện:
Bài
1:
Một con lắc đơn dao động điều hòa với chu kì 1 s trên mặt đất. Bán kính của
Trái Đất là 6400 km. Nếu đưa nó lên độ cao 20 km (xem chiều dài không thay đổi)
thì chu kì dao động điều hòa của nó sẽ:
A.
tăng 0,156% B. giảm
0,156% C. tăng
0,3125% D. giảm
0,3125%
Bài
2:
Một con lắc đơn dao động nhỏ với chu kì 2,032 s. Nếu giảm chiều dài 0,3% và giảm
gia tốc trọng trường 0,3% thì chu kì dao động bằng bao nhiêu?
A.
2,023 s B. 2,019
s C. 2,016
s D. 2,032
s
Bài
3:
Một con lắc đơn dao động điều hòa với chu kì 2,4495 s trên mặt đất. Đem con lắc
lên Mặt Trăng mà không thay đổi chiều dài thì chu kì dao động của nó là bao
nhiêu? Biết gia tốc rơi tự do trên Mặt Trăng bằng 1/6 gia tốc rơi tự do trên
Trái Đất.
A.
0,5 s B. 1 s C. 2 s D. 4 s
Bài
4:
Một con lắc đơn đếm giây có chu kì bằng 2 s ở nhiệt độ ${{0}^{0}}C$ và ở nơi có
gia tốc trọng trường là 9,8 $m/{{s}^{2}}$. Tính chu kì con lắc ở cùng vị trí
nhưng có nhiệt độ ${{25}^{0}}C$. Biết hệ số nở dài của dây treo con lắc là $1,{{2.10}^{-5}}$
(1/K).
A.
2,32 B. 2,032 C. 2,003 D. 2,0003
Bài
5:
Người ta nâng một con lắc đơn từ mặt đất lên độ cao 0,64 km. Biết bán kính Trái
Đất là 0,64 km, hệ số nở dài của thanh treo con lắc là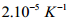 
. Hỏi nhiệt độ phải thay đổi thế nào để chu kì không thay đổi?
A.
tăng ${{10}^{0}}C$ B. giảm ${{10}^{0}}C$ C. tăng ${{5}^{0}}C$ D. giảm ${{5}^{0}}C$
Bài
6:
Một đồng hồ con lắc chạy đúng giờ khi đặt trên mặt đất ở nhiệt độ ${{25}^{0}}C$.
Biết hệ số dãn nở vì nhiệt của dây treo con lắc là ${{10}^{-4}}{{K}^{-1}}$, bán
kính Trái Đất là 6400 km. Nếu đưa con lắc xuống độ sâu 6,4 km so với bề mặt
Trái Đất và ở nhiệt độ ${{45}^{0}}C$ thù mỗi ngày đêm đống hồ sẽ chạy:
A.
nhanh 129,6 s B. chậm
86,4 s C. nhanh
86,4 s D. chậm
129,6 s
Bài
7:
Một đồng hồ quả lắc được xem như con lắc đơn mỗi ngày chạy nhanh 86,4 s. Phải
điều chỉnh chiều dài của dây treo như thế nào để đồng hồ chạy đúng?
A.
tăng 0,2% B. giảm
0,2% C. tăng
0,4% D. giảm
0,4%
Bài
8:
Một đồng hồ quả lắc được điều khiển bởi con lắc đơn chạy đúng giờ khi đặt ở địa
cực Bắc có gia tốc trọng trường 9,832 $m/{{s}^{2}}$. Đưa đồng hồ về xích đạo có
gia tốc trọng trường 9,78 $m/{{s}^{2}}$ thì trong một ngày đêm nó chạy nhanh
hay chậm bao nhiêu? Biết nhiệt độ không thay đổi.
A.
chậm 229,38 s B.
nhanh 210,72 s C. nhanh
60,72 s D. chậm
210,01 s
Bài
9:
Dùng con lắc đơn có chiều dài 1 m để điều khiển đồng hồ quả lắc thì đồng hồ chạy
đúng giờ. Do sơ suất khi bảo dưỡng nên đã làm giảm chiều dài thanh treo 0,2 mm.
Hỏi đồng hồ chạy nhanh hay chậm bao nhiêu sau một ngày đêm?
A.
nhanh 20,25 s B.
nhanh 8,64 s C. nhanh
10,52 s D. chậm
10,52 s
Bài
10:
Cho một con lắc đơn treo ở đầu một sợi dây mảnh dài bằng kim loại, vật nặng làm
bằng chất có khối lượng riêng 8$g/c{{m}^{3}}$. Khi dao động nhỏ trong bình chân
không thì chu kì dao động là 2 s. Cho con lắc đơn dao động trong bình chứa một
chất khí thì thấy chu kì tăng một lượng 250 $\mu s$. Khối lượng riêng của chất
khí đó là:
A.
0,004 $g/c{{m}^{3}}$ B. 0,002 $g/c{{m}^{3}}$ C. 0,04 $g/c{{m}^{3}}$ D. 0,02 $g/c{{m}^{3}}$
Đáp
án:
