A. Lí Thuyết Cần nhớ
1. Quãng đường vật đi được từ thời điểm t1 đến
t2 : Dt = t2 – t1
Tư
duy loại này: trong thời gian T/2 ( góc quay trên vòng tròn là: p
) vật dao động điều hòa sẽ đi được quãng đường là 2A. Ta dễ xác định quãng đường
đi được nếu thời gian là nhỏ hơn T/2 ( góc quay nhỏ hơn p
) dựa vào vòng tròn lượng giác.
Cách
làm
Bước bắt buộc: Tìm vị trí ban đầu: t = t1
tìm x1 và v1 ( chỉ quan tâm >0 hay <0 hay = 0)
Cách 1: Tách Dt theo T/2
$\frac{2\Delta
t}{T}=n,p=n+0,p$
( như vậy thời
gian vật đi xẽ là Dt
=nT/2 + 0,pT/2)
Vậy quãng đường
vật đi là S = n2A + S’
S’
là quãng đường vật đi được trong thời gian 0,pT/2 kể từ vị trí x1, v1.
Để xác định nó ta dùng vòng tròn lượng giác ( góc quay từ vị trí ban đầu Dj = w0,pT/2 = p.0,p)
Cách 2: Tìm ngay góc quay.
$\frac{\omega
\Delta t}{\pi }=n,p=n+0,p$ ( như vậy để đi hết thời gian Dt trên vòng
tròn sẽ quay góc np + 0,pp)
-
khi quay góc np vật đi được quãng đường n2A
-
khi quay góc Dj = p.0,p từ vị trí ban đầu ( x1, v1)
ta dựa vào vòng trọn lượng giác ta tìm được quãng đường đi là S’
-
vậy quãng đường vật đi được là S = n2A +
S’
( Nếu không thích tính theo T/2 ( góc quay p) thì các em có thể làm tính theo T ( góc quay 2p) nhưng phải nhớ là trong một T ( góc quay 2p) vật đi được quãng đường là 4A)
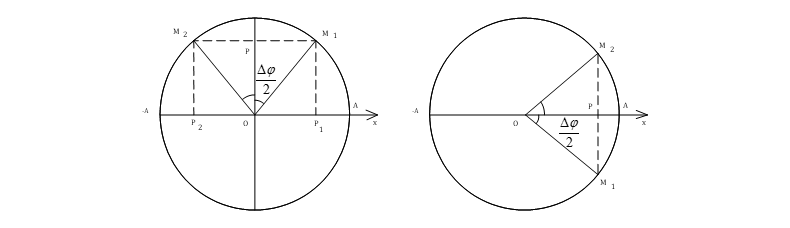
Bài toán tính quãng đường lớn nhất và nhỏ nhất vật đi được trong khoảng thời gian 0 < Dt < T/2.
- Vật có vận tốc
lớn nhất khi qua VTCB, nhỏ nhất khi qua vị trí biên nên trong cùng một khoảng
thời gian quãng đường đi được càng lớn khi vật ở càng gần VTCB và càng nhỏ khi
càng gần vị trí biên.
- Sử dụng mối
liên hệ giữa dao động điều hoà và chuyển
động tròn đều. Góc quét Dj = wDt.
- Quãng đường
lớn nhất khi vật đi từ M1 đến M2 đối xứng qua trục sin
(hình 1)
${{S}_{\text{max}}}=2\text{A}\sin
\frac{\Delta \varphi }{2}=2A\sin \frac{\omega \Delta t}{2}$
-
Quãng đường nhỏ nhất khi vật đi từ M1 đến M2 đối xứng qua
trục cos (hình 2)
${{S}_{min}}=2A(1-c\text{os}\frac{\Delta \varphi }{2})=2A(1-c\text{os}\frac{\omega \Delta t}{2})$
- Lưu ý: Trong trường hợp Dt
> T/2
Tách $\Delta t=n\frac{T}{2}+\Delta t'$ trong đó $n\in {{N}^{*}};0<\Delta
t'<\frac{T}{2}$
+
Trong thời gian $n\frac{T}{2}$ quãng đường luôn là 2nA
+
Trong thời gian Dt’ thì quãng đường lớn nhất, nhỏ nhất
tính như trên.
${{S}_{\text{max}}}=n2A+2\text{A}\sin
\frac{\Delta {{\varphi }^{'}}}{2}=n2A+2A\sin \frac{\omega \Delta {{t}^{'}}}{2}$
${{S}_{min}}=n2A+2A(1-c\text{os}\frac{\Delta
{{\varphi }^{'}}}{2})=n2A+2A(1-c\text{os}\frac{\omega \Delta {{t}^{'}}}{2})$
+
Tốc độ trung bình của vật đi từ thời điểm t1 đến t2: $\left|
{{v}_{tb}} \right|=\frac{S}{{{t}_{2}}-{{t}_{1}}}$ với S là quãng đường tính như
trên.
+
Vận tốc trung bình của vật \[{{v}_{tb}}=\frac{\left| {{x}_{2}}-{{x}_{1}}
\right|}{{{t}_{2}}-{{t}_{1}}}\]
+ Tốc độ trung bình lớn nhất và nhỏ
nhất của trong khoảng thời gian Dt:
${{v}_{tb\,m\text{ax}}}=\frac{{{S}_{\text{max}}}}{\Delta
t}$ và ${{v}_{tb\,min}}=\frac{{{S}_{min}}}{\Delta t}$ với Smax; Smin
tính như trên.
( Nếu bài toán nói thời gian nhỏ nhất đi được quãng đường S thì ta vẫn dùng các công thức trên để làm với S = Smax; Nếu bài toán nói thời gian lớn nhất đi được quãng đường S thì ta vẫn dùng các công thức trên để làm với S = Smin ; nếu muốn tìm n thì dùng \[\frac{S}{2A}=n,p(n+0,p)\])
B. BT Tự Luyện
Câu 1: Một vật
dao động điều hòa với phương trình \[x=5sin\left( 20\pi t \right)\] cm. Tốc độ
trung bình trong 1/4 chu kì kể từ lúc vật bắt đầu dao động là
A.\[{{v}_{tb}}=\pi \left( m/s \right).\] B.\[{{v}_{tb}}=\text{ }2\pi \left( m/s \right).\]
C.\[{{v}_{tb}}=\text{ }2/\pi \left( m/s
\right).\] D. \[{{v}_{tb}}=\text{ }1/\pi \left(
m/s \right).\]
Hướng dẫn giải
Tại thời điểm t=0 vật đang ở vị
trí cân bằng theo chiều dương
Quãng đường vật đi được sau 1/4 chu kì là \[S=A=5cm\]
Tốc độ trung bình trong 1/4 chu kì là \[{{v}_{tb}}=\frac{S}{t}=\frac{5}{\frac{\pi
}{40}}=\frac{200}{\pi }\left( cm/s \right)=\frac{2}{\pi }\left( m/s \right)\]
→Đáp án C.
Câu 2: Một vật dao động điều hòa với phương trình x =
4cos(2πt – π/3) cm. Tốc độ trung bình cực đại mà vật đạt được trong khoảng thời gian
2/3 chu kỳ dao động là
A. 18,92 cm/s. B. 18
cm/s. C. 13,6 cm/s. D. 15,39 cm/s.
Hướng dẫn giải
Ta có : \[T=1s\]
Quãng đường cực đại vật đi được trong khoảng thời gian 2/3 chu kì là \[S=2A+S{{'}_{max}}\]
\[\Rightarrow
S{{'}_{max}}=2A\sin \frac{\pi \Delta t}{T}=2A\sin \frac{\pi \frac{T}{6}}{T}=A\]\[\Rightarrow
S=3A\]
Tốc độ trung bình cực đại mà vật đạt được
trong khoảng thời gian 2/3 chu kì dao động là
\[{{v}_{tb}}=\frac{S}{A}=\frac{3A}{\frac{2T}{3}}=18cm/s\]→Đáp án B.
Câu 3: Một vật dao động điều hòa với phương trình x = 4cos(2πt – π/3)
cm. Tốc độ trung bình cực tiểu mà vật đạt được trong khoảng thời gian 2/3 chu kỳ
dao động là
A. 18,92 cm/s. B. 18
cm/s. C. 13,6 cm/s. D. 15,51 cm/s.
Hướng dẫn giải
Ta có : \[\frac{2T}{3}=\frac{T}{2}+\frac{T}{6}\]
Quãng đường cực tiểu mà vật đi được trong khoảng thời gian 2/3 chu kì : \[S=2A+S{{'}_{\min
}}\]
\[\Rightarrow
S{{'}_{\min }}=2A\left( 1-cos\frac{\pi \Delta t}{T} \right)=2A\left(
1-cos\frac{\pi }{6} \right)=\left( 2-\sqrt{3} \right)A\]\[\Rightarrow
S=2A+\left( 2-\sqrt{3} \right)A=9,07cm\]
Tốc độ trung bình cực tiểu mà vật đạt được
trong khoảng thời gian 2/3 chu kỳ dao động là
\[{{v}_{tb}}=\frac{{{S}_{tb}}}{t}=\frac{9,07}{\frac{2}{3}}=13,6cm/s\]
→Đáp án C.
Câu 4: Một vật dao động điều
hòa với chu kỳ T và biên độ A. Khi vật đi thẳng (theo một chiều) từ li độ x = A
đến li độ x = –A/2 thì tốc độ trung bình
của vật bằng
A. 9A/2T. B.
4A/T. C.
6A/T. D.
3A/T.
Hướng dẫn giải
Quãng đường vật đi được từ li độ x =
A đến li độ x = -A/2 là \[S=A+\frac{A}{2}=\frac{3A}{2}\]
Thời gian vật đi từ li độ x = A đến li độ x = -A/2 là : \[t=\frac{T}{4}+\frac{T}{12}=\frac{T}{3}\]
Tốc độ trung bình của vật : \[{{v}_{tb}}=\frac{S}{t}=\frac{\frac{3A}{2}}{\frac{T}{3}}=\frac{9A}{2}\]
→Đáp án A.
Câu 5: Một vật dao động điều hòa với biên độ 10cm,
chu kì 3s. Trong khoảng thời gian ngắn nhất khi vật đi từ vị trí cân bằng theo
chiều âm đến vị trí có li độ x = $5\sqrt{3}$ cm theo chiều âm, vật có tốc độ
trung bình là
A. 11,34 cm/s B. 12,54
cm/s C. 17,32
cm/s D. 20,96 cm/s
Hướng dẫn giải
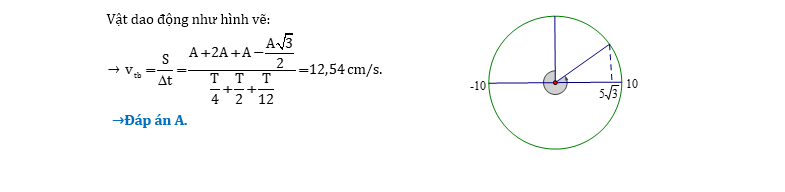
Câu 6: Một chất điểm dao động điều
hòa với chu kỳ T. Trong quá trình dao động, tỉ số giữa tốc độ trung bình nhỏ nhất
và tốc độ trung bình lớn nhất của chất điểm trong cùng khoảng thời gian \[\frac{2T}{3}\]
là
A.
\[5-3\sqrt{2}.\] B. \[\frac{4-\sqrt{3}}{3}.\] C. \[\sqrt{2}-1.\] D. \[\frac{\sqrt{3}}{3}.\]
Hướng dẫn giải
∆t
=$\frac{2T}{3}=\frac{T}{2}+\frac{T}{6}$ → \[\frac{{{v}_{tb\left( \frac{2T}{3}
\right)-\min }}}{{{v}_{tb\left( \frac{2T}{3} \right)-\max }}}=\frac{{{S}_{\min
\left( \frac{2T}{3} \right)}}}{{{S}_{\max \left( \frac{2T}{3}
\right)}}}=\frac{2A+2A\left( 1-\cos \frac{\pi }{6} \right)}{2A+2A\sin \frac{\pi
}{6}}=\frac{4-\sqrt{3}}{3}\].
→Đáp án B.
Câu 7: Một
vật thực hiện dao động điều hòa với biên độ 4 cm. Tốc độ trung bình lớn nhất mà
vật chuyển động trên quãng đường $4\sqrt{3}$cm là $0,3\sqrt{3}$m/s.
Chu kì dao động của vật là:
A. 0,1 s. B. 0,4 s. C. 0,3 s. D. 0,2 s.
Hướng dẫn giải
Quãng đường phải đi không đổi, để tốc độ trung
bình lớn nhất thì thời gian dao động phải nhỏ nhất.
Do đó:
∆tmin = $\frac{S}{{{v}_{tb-\max
}}}=\frac{2}{15}s$
Quãng đường $4\sqrt{3}$
< 2A → $4\sqrt{3}=2A\sin
\frac{\pi \Delta {{t}_{\min }}}{T}\to \Delta {{t}_{\min
}}=\frac{T}{3}=\frac{2}{15}\to T=0,4\text{ s}\text{.}$
→Đáp án B.
Câu 8: Một
vật dao động điều hoà với chu kỳ T và biên độ A, tốc độ trung bình bé nhất của
vật khi thực hiện được quãng đường 5A là
A.$\frac{6A(2-\sqrt{3})}{T}$. B.
$\frac{5A}{2T}$. C. $\frac{15A}{4T}$. D.
$\frac{5A}{T}$.
Hướng dẫn giải
Muốn tốc độ trung bình bé nhất thì
5A phải thực hiện trong khoảng thời gian lớn nhất.
5A = 2.2A + A → 4A luôn mất T, A thực hiện trong khoảng thời gian dài nhất
là:
$A=2A\left( 1-\cos \frac{\pi \Delta {{t}_{\max }}}{T} \right)\to \Delta
{{t}_{\max }}=\frac{T}{3}$
Vậy khoảng thời gian lớn nhất để vật
đi được quãng đường 5A là: \[T+\frac{T}{3}=\frac{4T}{3}\]
Tốc độ trung bình bé nhất cần tìm: ${{v}_{tb-\min
}}=\frac{5A}{\frac{4T}{3}}=\frac{15A}{4T}$
→Đáp án C.
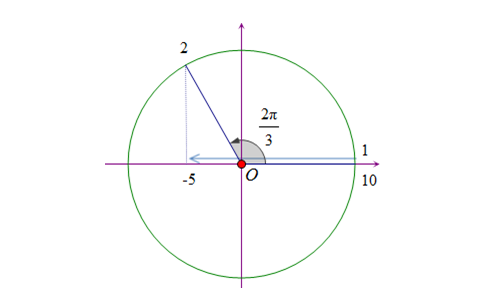
Câu 9: Một vật dao động điều hòa với phương trình
x = 10cos(2πt + π/6) cm. Khi vật đi từ li độ x = 10 cm đến
li độ x = –5 cm thì tốc độ trung bình của vật là
A. 45 cm/s. B. 40 cm/s. C. 50 cm/s. D. 30 cm/s.
Hướng dẫn giải
Ta
có: $\omega =2\pi (rad/s)\Rightarrow T=\frac{2\pi }{\omega }=1(s)$
Quãng đường vật đi được là $S=10+5=15(cm)$
|
Dựa
vào hình vẽ, ta thấy $\Delta
\varphi =\frac{2\pi }{3}(rad)\Rightarrow \Delta \varphi =\frac{2\pi
}{3}=\omega .\Delta t\Rightarrow \Delta t=\frac{\Delta \varphi }{\omega
}=\frac{T}{3}=\frac{1}{3}(s)$ Vận tốc trung bình của vât: $\overline{{{v}_{tb}}}=\frac{S}{\Delta t}=\frac{15}{\frac{1}{3}}=45(cm/s)$ →Đáp án A. | ||
Câu 10: Một chất điểm M dao động điều hòa theo phương trình x = 2,5cos(10πt + π/2) cm. Tốc độ trung bình của M trong 1 chu kỳ dao
động là A. 50 m/s. B. 50 cm/s. C. 5 m/s. D. 5 cm/s.
Hướng dẫn giải Ta có: $\omega =10\pi
(rad/s)\Rightarrow T=\frac{2\pi }{\omega }=0,2(s)$ Trong 1 chu kỳ quãng đường vật đi được:
$S=4A=4.2,5=10(cm)$ Tốc độ trung bình của M là $\overline{{{v}_{tb}}}=\frac{S}{\Delta
t}=\frac{S}{T}=\frac{10}{0,2}=50(cm/s)$ →Đáp án B. |







