Đại cương con lắc đơn
A.Kiến thức cơ bản
* Khảo sát con
lắc dao động điều hòa:
Điều kiện để con lắc
dao động điều hòa là góc lệch cực đại của dây treo \[{{\alpha }_{0}}\le
{{10}^{0}}\]
(hay \[{{\alpha }_{0}}<<1\]). Lúc này có
thể coi vật nặng dao động điều hòa trên đoạn thẳng BB’:
+ Phương
trình dao động của con lắc: \[s={{S}_{0}}\cos (\omega t+\varphi )\]
Với \[S=\alpha l\] là li
độ dao động
\[{{S}_{0}}={{\alpha }_{0}}l\]là biên độ
dao động
\[=>\]Phương trình dao động theo li độ góc \[\alpha
={{\alpha }_{0}}\cos (\omega t+\varphi )\]
Với \[\alpha \] là li độ
dao động
\[{{\alpha }_{0}}\] là biên độ dao động
+ Phương trình sao động vận tốc: \[v={s}'=-\omega
{{S}_{0}}\cos (\omega t+\varphi )\]
ð \[\left| {{v}_{\max }} \right|=\omega
{{S}_{0}}=\sqrt{gl}{{\alpha }_{0}}\]: Khi vật đi qua vị trí cân bằng
+Phương
trình gia tốc: \[a={v}'=-{{\omega
}^{2}}{{S}_{0}}\cos (\omega t+\varphi )\]
ð \[\left| {{a}_{\max }} \right|={{\omega
}^{2}}{{S}_{0}}=g{{\alpha }_{0}}\]( ở hai biên)
*Lực
kéo về của con lắc đơn: \[{{F}_{kv}}=ma=-m{{\omega
}^{2}}s=-ma\alpha \]
ð \[\left| {{F}_{kv\max }} \right|=m{{\omega
}^{2}}{{S}_{0}}=mg{{\alpha }_{0}}\]
* Năng
lượng dao động điều hòa của con lắc đơn:
Chọn gốc thế năng tại vị trí cân bằng.
+Thế năng: \[{{E}_{t}}=\frac{m{{\omega
}^{2}}{{s}^{2}}}{2}=\frac{mgl{{\alpha }^{2}}}{2}\]
+ Động năng: \[{{E}_{d}}=\frac{m{{v}^{2}}}{2}\]
+ Cơ năng: \[E={{E}_{t}}+{{E}_{d}}=>E={{E}_{t\max
}}=\frac{m{{\omega }^{2}}{{S}_{0}}^{2}}{2}=\frac{mgl{{\alpha }_{0}}^{2}}{2}\]và
\[E={{E}_{d\max }}=\frac{mv_{\max }^{2}}{2}\]
Chú ý: Khi \[{{E}_{d}}=n{{E}_{t}}=>s=\pm
\frac{{{S}_{0}}}{\sqrt{n+1}};\alpha =\pm \frac{{{\alpha
}_{0}}}{\sqrt{n+1}};v=\pm \sqrt{\frac{n}{n+1}}{{v}_{\max }}\]
B. BÀI
TẬP:
Câu 1: Một
con lắc đơn có dây treo dài 20 cm. Kéo con lắc lệch khỏi vị trí cân bằng một
góc 0,1 rad rồi cung cấp cho nó vân tốc \[10\sqrt{2}\] hướng theo phương vuông
góc với sợi dây. Bỏ qua ma sát, lấy \[g=10\,m/{{s}^{2}}\]. Biên độ dài của con lắc
bằng bao nhiêu?
Hướng dẫn:
Tần số góc \[\omega
=\sqrt{\frac{g}{l}}=\sqrt{50}=5\sqrt{2}\,\]rad/s.
Khi \[\alpha =0,1\]
rad \[=>s=\alpha l=2\,cm\];\[v=10\sqrt{2}\] cm/s
ð
Biên độ \[{{S}_{0}}=\sqrt{{{s}^{2}}+{{\left(
\frac{v}{\omega } \right)}^{^{2}}}}=2\sqrt{2}\](cm)
Câu 2: Tại nơi có gia tốc trọng trường g, một con lắc
đơn dao động điều hòa với biên độ \[{{\alpha }_{0}}\] nhỏ. Lấy mốc thế năng ở vị
trí cân bằng. Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có
động năng bằng thế năng thì li độ góc \[\alpha \] của con lắc bằng bao nhiêu?
Hướng dẫn:
Động năng bằng thế
năng khi \[\alpha =\pm \frac{{{\alpha }_{0}}}{\sqrt{2}}\]
Con lắc đang chuyển động nhanh dần theo chiều
dương => Vật nặng đang từ biên âm về vị trí cân bằng \[=>\alpha
=-\frac{{{\alpha }_{0}}}{\sqrt{2}}\].
Câu 3:
Tại một nơi có gia tốc trọng trường \[g={{\pi }^{2}}\,m/{{s}^{2}}\], con lắc
đơn dao động điều hòa trên quỹ đạo có thể coi là thẳng. Hai thời điểm liên tiếp
vật năng của con lắc đơn qua vị trí cân bằng là cách nhau 1s. Quãng đường vật nặng
đi được giữa hai thời điểm liên tiếp là 10 cm. Góc lệch cực đại của dây treo bằng
bao nhiêu?
Hướng dẫn:
+Thời gian giữa hai lần liên tiếp vật qua vị
trí cân bằng là \[\frac{T}{2}=1\,s\]
ð T=2 s => Chiều dài dây
treo là l=1 m
+Quãng đường vật đi được
khi đó \[S=2{{S}_{0}}=10\,cm=>{{S}_{0}}=0,05\,m\]
ð Góc lệch cực đại của dây treo là \[{{\alpha
}_{0}}=\frac{{{S}_{o}}}{l}=0,05\,rad\]
Câu 4:
Một con lắc đơn dao động điều hòa. Gốc thế năng được chọn tại vị trí cân bằng.
Khi góc lệch của dây treo bằng nữa góc lệch cực đại thì thế năng của con lắc là
\[{{2.10}^{-3}}\]J. Cơ năng của con lắc bằng bao nhiêu?
Hướng dẫn
Khi góc lệch dây treo bằng nữa góc lệch cực đại
(\[\alpha =\frac{{{\alpha }_{0}}}{2}\]) thì \[{{E}_{d}}=3{{E}_{t}}\]
\[=>E=4{{E}_{t}}={{8.10}^{-3}}\,J\]
Câu 5:
Một con lắc đơn (l=20gcm; m=100 g) treo tại nơi có \[g=9,8\,m/{{s}^{2}}\]. Kéo
con lắc khỏi phương thẳng đứng góc \[\alpha =0,1\,rad\], rồi chuyền cho con lắ
một vận tốc \[{{v}_{0}}\] theo phương vuông góc sợi dây về vị trí cân bằng. Chọn
gốc thế năng ở vị trí cân bằng, thế năng khi vật đã đi được quãng đường 4cm (kể
từ lúc truyền vận tốc cho con lắc ) bằng bao nhiêu?
Hướng dẫn:
Khi \[\alpha =0,1\,rad=>\,s=\alpha
l=2\,cm\]
Khi vật đi được quãng đường 4 cm(kể từ lúc
truyền vận tốc cho con lắc, vận tốc
\[{{v}_{0}}\] theo phương vuông góc sợi dây về
vị trí cân bằng) thì li độ s=-2 cm nên:
\[{{E}_{t}}=\frac{m{{\omega
}^{2}}{{s}^{2}}}{2}=\frac{mgl{{\alpha }^{2}}}{2}={{9,8.10}^{-4}}\,J\]
Câu 6:
Con lăc đơn có chiều dài 1 m, \[g=10m/{{s}^{2}}\], chọn gốc thế năng tại vị trí
cân bằng. Con lắc dao động với biên độ \[{{\alpha }_{0}}={{6}^{0}}\]. Tốc đọ của
vật tại vị trí mà thế năng bằng 3 lần động năng bằng bao nhiêu?
Hướng dẫn:
\[{{6}^{0}}=\frac{6\pi }{180}=\frac{\pi
}{30}\,rad\]
Khi \[{{E}_{t}}=3{{E}_{d}}=>\,{{E}_{d}}=\frac{{{E}_{t}}}{3}\]thì \[\left| v \right|=\sqrt{\frac{n}{n+1}}{{v}_{\max }}=\sqrt{\frac{\frac{1}{3}}{\frac{1}{3}+1}}\omega {{S}_{0}}=\frac{\sqrt{gl}{{\alpha }_{0}}}{2}=0,165\,m/s\]
Câu 7:
Một con lắc đơn(vật nặng có khối lượng m=100g) dao động điều hòa với phương
trình \[\alpha =0,05cos4t\,(rad)\]. Lấy \[g=10m/{{s}^{2}}\]. Tính thế năng khi
tốc độ của phương trình bằng 6,25 m/s.
Hướng dẫn:
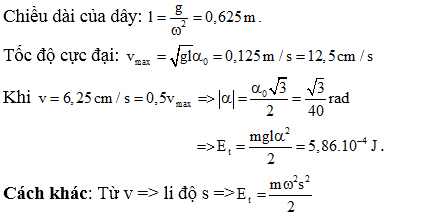
Câu 8:
Một con lắc đơn dao động nhỏ: Cứ sau khi vật nặng đi dược quãng đường ngắn nhất
bằng 4 cm thì động năng lại bằng 3 lần thế năng. Khoảng thời gian giữa hai lần
liên tiếp tốc độ của vật đạt cực đại là 0,25 s. Khoảng thời gian ngắn nhất để
nó đi từ vị trí có tốc độ \[8\pi \] cm/s đến vị trí có tốc độ \[8\pi \sqrt{3}\]
bằng bao nhiêu?
Hướng dẫn:
+Cứ sau khi vật nặng đi dược quãng đường ngắn
nhất bằng 4 cm thì động năng lại cứ bằng 3 lần thế năng \[=>{{S}_{0}}=4\,cm\]
+Khoảng thời gian giữa hai lần liên tiếp tốc
ddoojj của ật đạt cực đại là 0,25 s=0,5T => T= 0,5s => \[\omega =4\pi \]
rad/s.
+Tốc độ cực đại \[{{v}_{\max }}=\omega
{{S}_{0}}=16\pi \,cm/s\]
+Khi \[v=8\pi \,cm/s=0,5{{v}_{\max }}\] thì \[\left|
s \right|=\frac{{{S}_{0}}\sqrt{3}}{2}\]
+Khi \[v=8\pi \sqrt{3}\,cm/s=\frac{{{v}_{\max
}}\sqrt{3}}{2}\] thì \[\left| s \right|=\frac{{{S}_{0}}}{2}=>\vartriangle
{{t}_{\min }}=\frac{T}{6}-\frac{T}{12}=\frac{T}{12}=\frac{1}{24}s\]
Câu 9:
Con lắc đơn có chiều dài 64 cm, treo tại nơi \[g={{\pi }^{2}}\,m/{{s}^{2}}\].
Đưa con lắc khỏi vị trí cân bằng 4 cm theo chiều dương rồi buông cho dao động.
Chọn t=0 là lúc buông vật, lập phương trình dao động của vật?
Hướng dẫn:
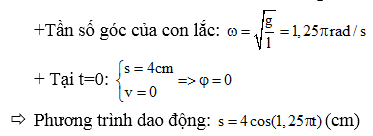
Câu 10:
Một con lắc đơn dao động điều hòa tại một nơi trên mặt đất. Viên bi đi theo một
chiều từ vị trí cao nhất đến vị trí thấp nhất mất 0,5s, đồng thời vạch trên một
cung tròn 5 cm. Chọn gốc thời gian lúc viên bi qua vị trí cân bằng theo chiều
dương. Lập phương trình dao động của con lắc đơn.
Hướng dẫn:

C. BÀI TẬP TỰ LUYỆN
Câu 1: Một con lắc đơn
dao động với biên độ góc nhỏ ( a0 < 150). Câu nào sau đây là sai đối với chu kì của
con
lắc ?
A. Chu kì phụ
thuộc chiều dài con lắc
B. Chu kì phụ
thuộc gia tốc trọng trường nơi có con lắc
C. Chu kì phụ
thuộc biên độ dao động
D. Chu kì
không phụ thuộc vào khối lượng của con lắc
Câu 2: Khi đưa một con lắc đơn lên cao theo phương thẳng
đứng (coi chiều dài của con lắc không
đổi) thì tần
số dao động điều hoà của nó sẽ
A. giảm vì gia
tốc trọng trường giảm theo độ cao.
B. tăng vì chu
kỳ dao động điều hoà của nó giảm.
C. tăng vì tần
số dao động điều hoà của nó tỉ lệ nghịch với gia tốc trọng trường.
D. không đổi
vì chu kỳ dao động điều hoà của nó không phụ thuộc vào gia tốc trọng trường
Câu 3: (CĐ 2007): Một con lắc đơn gồm sợi dây có khối
lượng không đáng kể, không dãn, có chiều dài l và viên bi nhỏ có khối lượng
m. Kích thích cho con lắc dao động điều hoà ở nơi có gia tốc trọng trường g. Nếu
chọn mốc thế năng tại vị trí cân bằng của viên bi thì thế năng của con lắc này ở
li độ góc α có biểu thức là
A. mg l (1 - cosα).
B. mg l (1 - sinα). C.
mg l (3 - 2cosα). D. mg
l (1 + cosα).
Câu 4: Phát biểu nào sau đây là sai khi nói về dao động
của con lắc đơn (bỏ qua lực cản của môi
trường)?
A. Khi vật nặng
ở vị trí biên, cơ năng của con lắc bằng thế năng của nó.
B. Chuyển động
của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần.
C. Khi vật nặng
đi qua vị trí cân bằng, thì trọng lực tác dụng lên nó cân bằng với lực căng của
dây.
D. Với dao động
nhỏ thì dao động của con lắc là dao động điều hòa.
Câu 5: Một con lắc đơn dao động điều hòa. Dây treo có
độ dài không đổi. Nếu đặt con lắc tại nơi có gia tốc rơi tự do là \[{{g}_{0}}\]
thì chu kỳ dao động là 1s. Nếu đặt con lắc tại nơi có gia tốc rơi tự do là g
thì chu kỳ dao động là
A.\[\frac{{{g}_{0}}}{g}\] B.\[\frac{g}{{{g}_{0}}}\] C.\[\sqrt{\frac{{{g}_{0}}}{g}}\] D.\[\sqrt{\frac{g}{{{g}_{0}}}}\]
Câu 6: Một con lắc đơn có chiều dài dây treo là ℓ,
dao động điều hòa với biên độ góc a0 (rad). Biên độ dao động của con lắc đơn là
A.\[l{{\alpha
}_{0}}\] B.\[\frac{l}{{{\alpha }_{0}}}\] C.\[\frac{{{\alpha
}_{0}}}{l}\] D.\[{{\alpha }_{0}}{{l}^{2}}\]
Câu 7: Tại nơi có gia tốc trọng trường g, một con lắc
đơn dao động điều hòa với biên độ góc a0. Biết khối
lượng vật nhỏ của con lắc là m, chiều dài dây treo là , mốc thế năng ở vị trí
cân bằng. Cơ năng củacon lắc là
A. \[\frac{1}{2}mgl{{\alpha
}_{0}}^{2}\] B.\[\frac{1}{4}mgl{{\alpha }_{0}}^{2}\] C.\[mgl{{\alpha }_{0}}^{2}\] D.\[\frac{1}{8}mgl{{\alpha
}_{0}}^{2}\]
Câu 8: Tại một vị trí trên Trái Đất, con lắc đơn có chiều
dài 1 dao động điều hòa với chu kì \[{{T}_{1}}\];con lắc đơn có chiều dài 2 ( \[{{l}_{2}}<{{l}_{1}}\])
dao động điều hòa với chu kì \[{{T}_{2}}\]. Cũng tại vị trí đó, con lắc đơn có
chiều dài
\[{{l}_{1}}-{{l}_{2}}\] dao động
điều hòa với chu kì là
A.\[\frac{{{T}_{1}}{{T}_{2}}}{{{T}_{1}}+{{T}_{2}}}\] B.\[\sqrt{T_{1}^{2}-T_{2}^{2}}\] C.\[\frac{{{T}_{1}}{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\] D.\[\sqrt{{{T}_{1}}^{2}+T_{2}^{2}}\]
Câu 9: Tại một nơi hai con lắc
đơn dao động điều hòa. Trong cùng một khoảng thời gian, người ta thấy con lắc thứ nhất
thực hiện được 4 dao động, con lắc thứ hai thực hiện được 5 dao động. Tổng chiều
dài của hai con lắc là 164 cm. Chiều dài của mỗi con lắc lần lượt là
A. l1 = 100 m, l2 = 6,4 m. B.
l1 = 64 cm, l2 = 100 cm .
C. l1 = 1,00 m, l2 = 64 cm D.
l1 = 6,4 cm, l2 = 100 cm.
Câu 10: Tại nơi có
gia tốc trọng trường g, một con lắc đơn có chiều dài dao động điều hòa với
chu kì 2,83
s. Nếu chiều dài của con lắc là 0,5 thì con lắc dao động với chu kì là
A. 1,42 s. B. 2,00 s. C. 3,14 s. D. 0,71 s.







