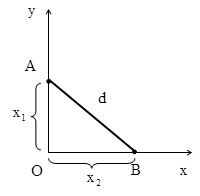BT CON LẮC LÒ XO ( trường chuyên)
Câu 1: (Chuyên Lam Sơn – 2017) Một con lắc lò xo treo thẳng đứng, vật nặng có khối lượng \[m=250\]g. Chọn trục tọa độ Ox thẳng đứng, chiều dương hướng xuống dưới, gốc tọa độ ở vị trí cân bằng. Vật được thả nhẹ từ vị trí lò xo giãn 6,5 cm. Vật dao động điều hòa với năng lượng 80 mJ. Lấy gốc thời gian là lúc thả vật và \[g=10\]m/s2. Phương trình dao động của vật là
A. \[x=6,5\cos \left( 5\pi t \right)\]cm B. \[x=4\cos \left( 5\pi t \right)\]cm
C. \[x=6,5\cos \left( 20t \right)\]cm D. \[x=4\cos \left( 20t \right)\]cm
Hướng dẫn
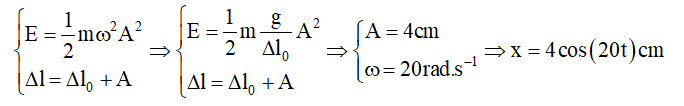
- Đáp án D
Câu 2:(Chuyên Vinh – 2017) Hai chất điểm dao động điều hòa trên hai đường thẳng song song gần kề nhau có vị trí cân bằng nằm trên cùng một đường thẳng vuông góc với quỹ đạo của chúng và có cùng tần số góc ω, biên độ lần lượt là A1, A2. Biết \[{{A}_{1}}+{{A}_{2}}=8\]cm. Tại một thời điểm vật 1 và vật 2 có li độ và vận tốc lần lượt là x1, v1 , x2, v2 và thỏa mãn \[{{x}_{1}}{{v}_{2}}+{{x}_{2}}{{v}_{1}}=8\]cm2.s. Giá trị nhỏ nhất của ω là
A. 0,5 rad/s B. 2 rad/s C. 1 rad/s D. 4 rad/s
Hướng dẫn
Ta có:
.png)
Mặc khác
\[{{x}_{1}}{{v}_{2}}+{{x}_{2}}{{v}_{1}}={{x}_{1}}{{{x}'}_{2}}+{{x}_{2}}{{{x}'}_{1}}={{\left( {{x}_{1}}{{x}_{2}} \right)}^{\prime }}=\frac{{{A}_{1}}{{A}_{2}}2\omega }{2}\sin \left( 2\omega t+{{\varphi }_{1}}+{{\varphi }_{2}} \right)=8\Rightarrow \omega =\frac{8}{{{A}_{1}}{{A}_{2}}\sin \left( 2\omega t+{{\varphi }_{1}}+{{\varphi }_{2}} \right)}\]Kết hợp với
\[{{A}_{1}}+{{A}_{2}}=8\xrightarrow[\text{Cos}i]{{{\left( {{A}_{1}}+{{A}_{2}} \right)}^{2}}\ge 4{{\text{A}}_{1}}{{A}_{2}}}{{\left( {{A}_{1}}{{A}_{2}} \right)}_{ma\text{x}}}=\frac{{{8}^{2}}}{4}=16\]
Vậy \[{{\omega }_{\min }}=\frac{8}{\underbrace{{{A}_{1}}{{A}_{2}}}_{\max =16}\underbrace{\sin \left( 2\omega t+{{\varphi }_{1}}+{{\varphi }_{2}} \right)}_{ma\text{x}=1}}=0,5\]
- Đáp án A
|
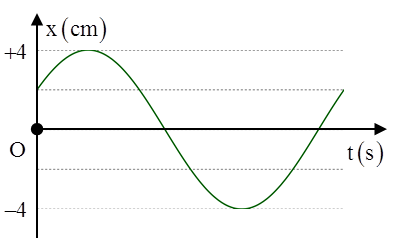
Câu 3:(Chuyên Vĩnh Phúc – 2017) Quả nặng có khối lượng 500 g gắn vào lò xo có độ cứng 50 N/m. Chọn gốc tọa độ tại vị trí cân bằng, kích thích để quả nặng dao động điều hòa. Đồ thị biểu diễn li độ theo thời gian như hình vẽ. Phương trình dao động của vật là A. \[x=8\cos \left( 10t+\frac{\pi }{6} \right)\]cm B. \[x=8\cos \left( 10t-\frac{\pi }{6} \right)\]cm C. \[x=8\cos \left( 10t+\frac{\pi }{3} \right)\]cm D. \[x=8\cos \left( 10t-\frac{\pi }{3} \right)\]cm Hướng dẫn Quan sát đồ thị ta thấy \[A=8cm\], tại thời điểm ban đầu vật đi qua vị trí \[\frac{A}{2}\] theo chiều dương nên pha ban đầu là \[-\frac{\pi }{3}\]
|
|
Câu 4:(Phan Bội Châu – 2017) Một vật nhỏ tham gia đồng thời hai dao động điều hòa cùng tần số góc bằng 10 rad/s, có phương trình li độ x1 và x2 thõa mãn \[28,8\text{x}_{1}^{2}+5\text{x}_{2}^{2}=720\](với x1 và x2 được tính bằng cm). Lúc li độ của dao động thứ nhất là \[{{x}_{1}}=3\]cm và li độ của vật đang dương thì tốc độ của vật bằng
A. 96 cm/s B. 63 cm/s C. 32 cm/s D. 45 cm/s
Hướng dẫn
Với \[28,8\text{x}_{1}^{2}+5\text{x}_{2}^{2}=720\Leftrightarrow \frac{x_{1}^{2}}{{{5}^{2}}}+\frac{x_{2}^{2}}{{{12}^{2}}}=1\]
Hai dao động này vuông pha nhau với biên độ dao động lần lượt là \[{{A}_{1}}=5\]cm và \[{{A}_{2}}=12\]cm
+ Tại \[{{x}_{1}}=3\]cm
.png)
+ Lấy đạo hàm hai vế ta thu được
\[57,6{{\text{x}}_{1}}{{v}_{1}}+10{{\text{x}}_{2}}{{v}_{2}}=0\xrightarrow[{{v}_{1}}=40]{{{x}_{2}}=9,6cm}{{v}_{2}}=72\]cm/s
Tốc độ của vật \[v={{v}_{1}}+{{v}_{2}}=32\]cm/s
- Đáp án C
|
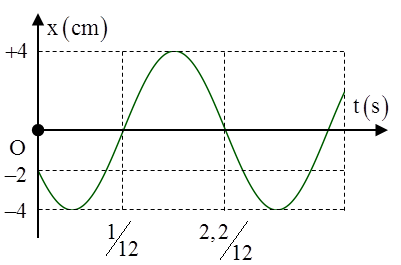
Câu 5:(Quốc Học – 2017) Hình vẽ là đồ thi biễu diễn độ dời của dao động x theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là A. \[x=4\cos \left( 10\pi t+\frac{2\pi }{3} \right)\]cm B. \[x=4\cos \left( 20\pi t-\frac{2\pi }{3} \right)\]cm C. \[x=4\cos \left( 10t+\frac{5\pi }{6} \right)\]cm D. \[x=4\cos \left( 20t-\frac{\pi }{3} \right)\]cm Hướng dẫn Chu kì dao động của vật \[\frac{T}{2}=\frac{2,2}{12}-\frac{1}{12}=\frac{1,2}{12}s\xrightarrow{\omega =\frac{2\pi }{T}}\omega =\frac{2\pi }{\frac{1,2}{12}}=20\pi \]rad/s Tại thơi điểm \[t=0\]
\[\Rightarrow \]\[x=4\cos \left( 20\pi t+\frac{2\pi }{3} \right)\]cm
|
|
Câu 6:(Nam Đàn – 2017) Hai chất điểm P, Q cùng xuất phát từ một vị trí và bắt đầu dao động điều hòa theo cùng một chiều trên trục ox (trên 2 đường thẳng song song kề sát nhau), cùng biên độ nhưng với chu kỳ lần lượt là T1 và \[{{T}_{2}}=2{{T}_{1}}\]. Tỷ số độ lớn vận tốc của P và Q khi chúng gặp nhau là:
A. \[\frac{1}{2}\] B. 2 C. \[\frac{3}{2}\] D. \[\frac{2}{3}\]
Hướng dẫn
Tỉ số tốc độ của hai chất điểm
\[\frac{{{v}_{P}}}{{{v}_{Q}}}=\frac{{{\omega }_{1}}\sin \left( {{\omega }_{1}}t+\varphi \right)}{{{\omega }_{2}}\sin \left( {{\omega }_{2}}t+\varphi \right)}=\frac{{{T}_{2}}\sin \left( {{\omega }_{1}}t+\varphi \right)}{{{T}_{1}}\sin \left( {{\omega }_{2}}t+\varphi \right)}=2\frac{\sin \left( {{\omega }_{1}}t+\varphi \right)}{\sin \left( {{\omega }_{2}}t+\varphi \right)}\]
Mặc khác khi hai chất điểm này gặp nhau thì
\[{{x}_{1}}={{x}_{2}}\Leftrightarrow \underbrace{\cos \left( {{\omega }_{1}}t+\varphi \right)}_{\sqrt{10-{{\cos }^{2}}\left( {{\omega }_{1}}t+\varphi \right)}}=\underbrace{\cos \left( {{\omega }_{2}}t+\varphi \right)}_{\sqrt{10-{{\cos }^{2}}\left( {{\omega }_{2}}t+\varphi \right)}}\Leftrightarrow \sin \left( {{\omega }_{1}}t+\varphi \right)=\sin \left( {{\omega }_{2}}t+\varphi \right)\]
Vậy \[\frac{{{v}_{P}}}{{{v}_{Q}}}=2\]
Đáp án B
Câu 7:(Chuyên Sp Hà Nội – 2017) Hai chất điểm A và B dao động trên hai trục của hệ trục tọa độ Oxy (O là vị trí cân bằng của 2 vật) với phương trình lần lượt là: \[{{x}_{A}}=4\cos \left( 10\pi t+\frac{\pi }{6} \right)cm\] và \[{{x}_{B}}=4\cos \left( 10\pi t+\frac{\pi }{3} \right)cm\]. Khoảng cách lớn nhất giữa A và B là:
A. 5,86 cm B. 5,26 cm C. 5,46 cm D. 5,66 cm
Hướng dẫn
|
Khoảng cách giữa hai chất điểm \[d=\sqrt{x_{A}^{2}+x_{B}^{2}}=4\sqrt{\underbrace{{{\cos }^{2}}\left( 10\pi t+\frac{\pi }{6} \right)+{{\cos }^{2}}\left( 10\pi t+\frac{\pi }{3} \right)}_{y}}\] Để d là lớn nhất thì y phải lớn nhất, biến đổi toán học ta thu được \[y=1+\frac{1}{2}\cos \left( 20\pi t+\frac{\pi }{3} \right)+\frac{1}{2}\cos \left( 20\pi t+\frac{2\pi }{3} \right)\] Sử dụng công thức cộng lượng giác \[y=1+\frac{\sqrt{3}}{2}\sin \left( 20\pi t \right)\Rightarrow {{y}_{ma\text{x}}}=1+\frac{\sqrt{3}}{2}\] Vậy \[{{d}_{ma\text{x}}}=4\sqrt{{{y}_{ma\text{x}}}}=4\sqrt{1+\frac{\sqrt{3}}{2}}\approx 5,46cm\] |
|
- Đáp án C
|
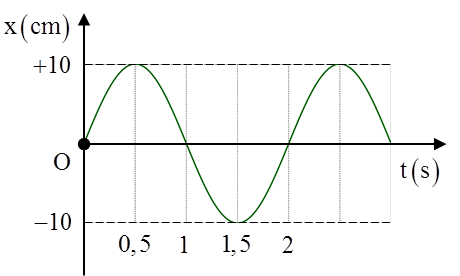
Câu 8: (Chuyên Lam Sơn) Một vật dao động điều hòa có li độ x được biểu diễn như hình vẽ. Cơ năng của vật là 250 J. Lấy \[{{\pi }^{2}}=10\]. Khối lượng của vật là: A. 5000 kg B. 500 kg C. 50 kg D. 0,5 kg
|
|
Hướng dẫn
Từ hình vẽ ta thu được \[A=10cm\] và \[T=2\text{s}\Rightarrow \omega =\pi ra\text{d}.{{s}^{-1}}\]
Cơ năng của con lắc
\[E=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Rightarrow m=\frac{2\text{E}}{{{\omega }^{2}}{{A}^{2}}}=\frac{2.250}{{{\left( \pi \right)}^{2}}{{\left( {{10.10}^{-2}} \right)}^{2}}}=5000kg\]
- Đáp án A
|
Câu 9:(Chuyên Hạ Long – 2017) Một chất điểm dao động điều hòa có li độ phụ thuộc thời gian theo hàm cosin như hình vẽ. Chất điểm có biên độ là: A. 4 cm B. 8 cm C. \[-4\]cm D. \[-8\]cm Hướng dẫn Dễ thấy rằng biên độ dao động của vật \[A=4cm\]
|
|
||||
|
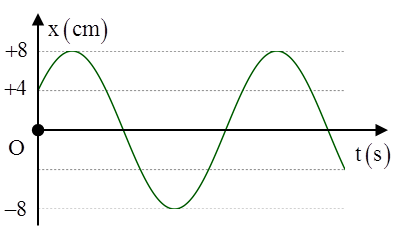
Câu 10:(Minh họa – 2017) Trên mặt phẳng nằm ngang có hai con lắc lò xo. Các lò xo. Các lò xo có độ cứng k, cùng có chiều dài tự nhiên là 32 cm. Các vật A và B có khối lượng lần lượt là m và 4m. Ban đầu, A và B được giữ ở vị trí sao cho lò xo gắn với A bị giãn 8 cm còn lò xo gắn với vật B bị nén 8 cm. Đồng thời thả nhẹ để hai vật dao động điều hòa trên cùng một đường thẳng đi qua giá đỡ I cố định (hình vẽ). Trong quá trình dao động, khoảng cách lớn nhất và nhỏ nhất giữa hai vật có giá trị lần lượt là A. 68 cm và 48 cm B. 80 cm và 48 cm C. 64 cm và 55 cm D. 80 cm và 55 cm Hướng dẫn Chọn hệ trục tọa độ như hình vẽ
\[d={{x}_{A}}-{{x}_{B}}=64+8\cos \left( 2\omega t \right)-8\cos \left( \omega t \right)\] Biến đổi lượng giác \[d=64+8\left[ 2\underbrace{{{\cos }^{2}}\omega t}_{{{x}^{2}}}-\underbrace{\cos \omega t}_{x}-1 \right]\] Khảo sát hàm số ta thu được: \[{{d}_{\min }}=55cm\] và \[{{d}_{max}}=80cm\]
|
|
|
|||
.png)