Các dạng toán về dao động điều hòa

CÁC DẠNG TOÁN DAO ĐỘNG ĐIỀU HÒA

Dạng 1: Tìm những thời điểm ứng với lúc vật có li độ x, vận tốc v,… xác định

- Thế giá trị của x hoặc v vào phương trình li độ hoặc phương trình vận tốc để tìm thời điểm t

* Chú ý: Để xác định chiều chuyển động ta dựa vào v

+) Nếu v>0 $\Rightarrow $ vật chuyển động (+)

+) Nếu v<0 $\Rightarrow $ vật chuyển động (-)

Ví dụ 1: Vật dao động điều hòa $x=2\cos (\pi t-\frac{\pi }{3})$ cm

a) Xác định những thời điểm ứng với lúc vật có li độ x=-1 cm. Suy ra thời điểm đầu tiên.

b) Xác định những thời điểm ứng với vật có li độ x=$\sqrt{3}$ cm theo chiều dương trong khoảng thời gian 2 chu kì đầu tiên

Hướng dẫn

a) Thế -1 vào phương trình dao động điều hòa, ta có:

$-1=2.\cos (\pi t-\frac{\pi }{3})\Leftrightarrow \cos (\pi t-\frac{\pi }{3})=cos\frac{2\pi }{3}$

\[\Leftrightarrow \pi t-\frac{\pi }{3}=\pm \frac{2\pi }{3}+k2\pi (k\in Z)\]

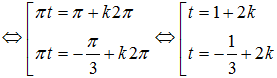
$\Leftrightarrow t=1(s)$

b) Thế t=0 vào phương trình dao động điều hòa nên ta có vị trí ban đầu của vật là x=1 cm

Theo đề bài ta có vật đi qua $\sqrt{3}$ theo chiều dương nên ta có :

\[{{t}_{1}}=\frac{T}{6}-\frac{T}{12}=\frac{T}{12}\]

${{t}_{2}}=\frac{T}{6}+\frac{T}{2}+\frac{T}{4}+\frac{T}{6}=\frac{13T}{12}$

Mà ta có: $T=\frac{2\pi }{\omega }=\frac{2\pi }{\pi }=2(s)$

Thế vào ta có: ${{t}_{1}}=\frac{1}{6}(s);{{t}_{2}}=\frac{13}{6}(s)$

Dạng 2: Tìm thời gian ngắn nhất đi từ ${{x}_{1}}\to {{x}_{2}}$

1, Nguyên tắc: Thời gian để vật dao động điều hòa đi từ li độ ${{x}_{1}}\to {{x}_{2}}$ bằng thời gian để điểm chuyển động tròn đều đi từ M$\to $ N

2. Cách tính

+) Tìm góc quay $\alpha =\widehat{MON}$

+) Tìm thời gian tương ứng

$\Delta t=\frac{\alpha (rad)}{\omega }$

* CHÚ Ý

Vật đi từ VTCB đến x hoặc ngược lại

$\Delta t=\frac{1}{\omega }\arcsin \frac{\left| x \right|}{A}$

Vật đi từ biên đến li độ hoặc ngược lại

$\Delta t=\frac{1}{\omega }\arccos \frac{\left| x \right|}{A}$

Có thể tính nhanh

Ví dụ 1: Một vật dao động điều hòa với biên độ A và tần số f = 5Hz. Xác định thời gian ngắn nhất để vật đi từ vị trí có li độ ${{x}_{1}}=\frac{A}{2}$ đến vị trí có li độ .${{x}_{2}}=-\frac{A}{2}$

Hướng dẫn

Ta có: $\omega =2\pi .f=10\pi (rad/s)$

Áp dụng công thức:

Ví dụ 2: Một vật dao động điều hoà theo phương trình: \[x\text{ }=\text{ }Acos(\omega t\text{ }~-\frac{\pi }{2})\]cm . Cho biết, từ thời điểm ban đầu vật đến li độ \[x~=~\frac{A\sqrt{3}}{2}\] trong khoảng thời gian ngắn nhất là$\frac{1}{60}$ s , và tại điểm cách VTCB 2(cm) vật có vận tốc$40\pi \sqrt{3}$ (cm/s). Xác định tần số góc và biên độ A của dao động.

Hướng dẫn

Ở thời điểm ban đầu (t1 = 0), vật có:x=0; v>0 (do $-\frac{\pi }{2}<0$ ) , tức là vật qua vị trí cân bằng theo chiều dương.

Ở thời điểm t2 = $\frac{1}{60}$s, vật qua li độ \[x{{~}_{2}}=~\frac{A\sqrt{3}}{2}\] theo chiều dương.

Nên ta có: $\frac{T}{6}=\frac{1}{60}\Rightarrow T=\frac{1}{10}\Rightarrow \omega =20\pi (rad/s)$

Áp dụng công thức: $A=\sqrt{{{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}}=\sqrt{{{2}^{2}}+\frac{{{(40\pi \sqrt{3})}^{2}}}{{{(20\pi )}^{2}}}}=4(cm)$

Dạng 3: Tìm quãng đường của vật dao động điều hòa trong 1 khoảng thời gian $\Delta t$ nhất định

1. Cần nhớ:

a) Quãng đường đi của vật trong

+) 1T luôn là 4A

+) $\frac{1}{2}T$ luôn là 2A

b) Sau $1T\Rightarrow {{x}_{2}}={{x}_{1}};{{v}_{2}}={{v}_{1}};{{a}_{2}}={{a}_{1}}$

Sau $\frac{T}{2}\Rightarrow {{x}_{2}}=-{{x}_{1}};{{v}_{2}}=-{{v}_{1}};{{a}_{2}}=-{{a}_{1}}$

2. Cách tính quãng đường đi

Bước 1: Ta cần biết

Bước 2: Ta phân tích thời gian $\Delta t$ đã cho thành:

$\Delta t={{n}_{1}}T+{{n}_{2}}\frac{T}{2}+\Delta t'$

Bước 3: Quãng đường cần tìm

$S={{n}_{1}}.4A+{{n}_{2}}.2A+{{S}_{(\Delta t')}}$

${{S}_{(\Delta t')}}$Thường được tìm từ mối liên hệ giữa chuyển động tròn đều và dao động điều hòa.

Ví dụ: 1 vật dao động điều hòa với phương trình: $x=10\cos (\frac{\pi }{3}t+\frac{\pi }{3})cm$ . Tìm quãng đường vật đi được trong mỗi khoảng thời gian sau:

a) 16 (s)

b) 13,5 (s)

c) 7,25 (s)

d) 19,7 (s)

Hướng dẫn

Áp dụng công thức : \[T=\frac{2\pi }{\omega }=\frac{2\pi }{{}^{\pi }/{}_{3}}=6(s)\]

Tại t=0 $\Rightarrow x=5$

Mà ta có: $\frac{\pi }{3}>0\Rightarrow v<0$

a) Ta có: $\frac{16}{6}=\frac{8}{3}$

$\Rightarrow \Delta t=2T+\frac{1}{2}T+\frac{1}{6}T$

$\Rightarrow 2.4A+2A+{{S}_{({}^{T}/{}_{6})}}=2.4.10+2.10+10=110(cm)$

b) Ta có: $\frac{13,5}{6}=\frac{9}{4}$

$\Rightarrow \Delta t=2T+\frac{1}{4}T$

$\Rightarrow 2.4A+{{S}_{({}^{T}/{}_{4})}}=2.4.10+5+5\sqrt{3}=85+5\sqrt{3}(cm)$

c) Ta có: $\frac{7,25}{6}=\frac{29}{24}$

$\Rightarrow \Delta t=T+\frac{5}{24}T$

$\Rightarrow 4A+{{S}_{({}^{5T}/{}_{24})}}=4.10+5+5\sqrt{2}=45+5\sqrt{2}(cm)$

d) Ta có: $\frac{19,7}{6}=\frac{197}{60}$

$\Rightarrow \Delta t=3T+\frac{17}{60}T$

$\Rightarrow 3.4A+{{S}_{({}^{17T}/{}_{60})}}=3.4.10+5+9,5=134,5(cm)$

Ví dụ 2 : Phương trình dao động điều hòa của vật x = 4cos(4πt +$\frac{\pi }{3}$) (cm); thời điểm vật đi qua vị trí x = 2$\sqrt{3}$ cm theo chiều dương lần thứ 2017 là

A. 504,25 s. B. 2016,25 s. C. 504,375 s. D. 1008,375 s.

Hướng dẫn:

T = $\frac{2\pi }{\omega }=\frac{2\pi }{4\pi }$= 0,5 (s). Khi t = 0 thì x = 4cos$\frac{\pi }{3}$ = 2 (cm) và đang chuyển động theo chiều âm. Khoảng thời gian để vật đi từ vị trí x = 2 cm = $\frac{A}{2}$ theo chiều âm đến

vị trí x = 2$\sqrt{3}$ cm = $\frac{A\sqrt{3}}{2}$ theo chiều dương lần thứ nhất là:

Dt = $\frac{T}{12}+\frac{T}{2}+\frac{T}{6}=\frac{3T}{4}=\frac{3.0,5}{4}$ = 0,375 (s).

Sau đó cứ mỗi chu kì vật đi qua vị trí có x = 2$\sqrt{3}$ cm = $\frac{A\sqrt{3}}{2}$ theo chiều dương một lần nên: t = Dt + 2016.T = 0,375 + 2016.05 = 1008, 375 (s). Đáp án D.

Dạng 4: Tìm quãng đương dài nhất và ngắn nhất mà vật đi được trong khoảng thời gian $\Delta t$ nhất định

1. Trường hợp 0 < $\Delta t$ < $\frac{T}{2}$

a) Quãng đường đi dài nhất ( lân cận VTCB)

${{S}_{\max }}=2A.\sin \frac{\varphi }{2}$

Với $\varphi =\omega .\Delta t=\frac{2\pi }{T}.\Delta t$ , nên:

${{S}_{\max }}=2A.\sin \frac{\pi .\Delta t}{T}$

b) Quãng đương đi ngắn nhất ( lân cân điểm biên )

${{S}_{\min }}=2A(1-\cos \frac{\varphi }{2})$

$\Rightarrow {{S}_{\min }}=2A(1-\cos \frac{\pi .\Delta t}{T})$

2, Trường hợp $\Delta t>\frac{T}{2}$

Ta phân tích $\Delta t={{n}_{1}}T+{{n}_{2}}.\frac{T}{2}+\Delta t'$ với $o<\Delta t'<\frac{T}{2}$

Ví dụ1: Một vật dao động điều hòa biên độ A và chu kỳ T. Trong khoảng thời gian \[\Delta t=\frac{T}{4}\] , quãng đường lớn nhất mà vật đi được là bao nhiêu?

Hướng dẫn:

\[\frac{T}{4}=2.\frac{T}{8}\to {{S}_{\max }}=2.\frac{A\sqrt{2}}{2}=A\sqrt{2}\]

Ví dụ 2: Một vật dao động điều hòa biên độ A và chu kỳ T. Trong khoảng thời gian \[\Delta t=\frac{3T}{4}\] , quãng đường nhỏ nhất mà vật đi được là bao nhiêu?

Hướng dẫn:

\[\frac{3T}{4}=\frac{T}{2}+\frac{T}{4}=\frac{T}{2}+2.\frac{T}{8}\to {{S}_{\min }}=2\text{A}+2\left( A-\frac{A\sqrt{2}}{2} \right)=2\text{A+A}\left( 2-\sqrt{2} \right)=A\left( 4-\sqrt{2} \right)\]

Dạng 5: Tính tốc độ trung bình

Chú ý: ${{v}_{tb(\min )}}\le {{v}_{tb}}\le {{v}_{tb(\max )}}$

Ví dụ: Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai, vật có tốc độ trung bình là

A. 27,3 cm/s. B. 28,0 cm/s. C. 27,0 cm/s. D. 26,7 cm/s.

Hướng dẫn:

A = $\frac{L}{2}$ = 7 cm; thời gian đi từ vị trí có x = 3,5 cm = $\frac{A}{2}$ theo chiều dương

đến khi gia tốc đạt giá trị cực tiểu lần thứ nhất (\[x\text{ }=\text{ }A;\text{ }a\text{ }=\text{ }-{{\omega }^{2}}x\text{ }=\text{ }-{{\omega }^{2}}A\]) là $\frac{T}{6}$; sau đó 1 chu kì nữa thì gia tốc đạt cực tiểu lần thứ hai nên \[\Delta t\] = $\frac{T}{6}$ + T = $\frac{7T}{6}$ = $\frac{7}{6}$s; quãng đường đi trong thời gian đó là \[\Delta S\] = $\frac{A}{2}$ + 4A = $\frac{9A}{2}$ = 31,5 cm.

Tốc độ trung bình là v = $\frac{\Delta s}{\Delta t}$ = 27 (cm/s). Đáp án C.

Dạng 6: Vấn đề liên quan đến các dao động điều hòa cùng tần số và vuông pha

Chú ý:

1. Khi khảo sát 1 vật dao động điều hòa ở 2 thời điểm ${{t}_{1}}$ và ${{t}_{2}}$ mà ${{t}_{2}}={{t}_{1}}+(2k+1)\frac{T}{4}$ thì li độ, vận tốc, gia tốc ở 2 thời điểm này sẽ vuông pha.

${{x}_{1}}$ và ${{x}_{2}}$

${{v}_{1}}$ và ${{v}_{2}}$

${{a}_{1}}$ và ${{a}_{2}}$

2. Ta có thể dung liên hệ giữa chuyển động đều và dao động điều hòa để giải quyết bài toán

Ví dụ 1: Hai vật dao động điều hòa trên hai đường thẳng cùng song song với trục Ox. Hình chiếu vuông góc của các vật lên trục Ox dao động với phương trình x₁ = 10cos(2,5\[\pi \]t + $\frac{\pi }{4}$) (cm) và x₂ = 10cos(2,5\[\pi \]t − $\frac{\pi }{4}$) (cm) (t tính bằng s). Kể từ t = 0, thời điểm hình chiếu của hai vật cách nhau 10 cm lần thứ 2018 là

A. 806,9 s. B. 403,2 s. C. 807,2 s. D. 403,5 s.

Hướng dẫn

T = $\frac{2\pi }{\omega }=\frac{2\pi }{2,5\pi }$ = 0,8 (s); \[\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}\] = -$\frac{\pi }{4}$- $\frac{\pi }{4}$= - $\frac{\pi }{2}$; hai dao động vuông pha và đều có biên độ 10 cm nên hình chiếu của hai vật cách nhau 10 cm khi hình chiếu của một trong hai dao động bằng 0; thời điểm đầu tiên (kể từ thời điểm t = 0) hình chiếu của một trong hai dao động bằng 0 (đó chính là x₁) là $\frac{T}{8}$ = 0,1 s; sau đó cứ mỗi chu kì (kể từ thời điểm t = $\frac{T}{4}$) có 4 lần hình chiếu của một trong hai dao động bằng 0 nên thời điểm để hình chiếu của hai vật cách nhau 10 cm lần thứ 2018 là $\frac{2016}{4}$T + $\frac{T}{8}$ +$\frac{T}{4}$= 504,375T = 504,375.0,8 = 403,5 (s). Đáp án D.

BÀI TẬP TỰ LUYỆN

Câu 1. Vật dao động điều hòa với chu kì 2 s, biên độ 10 cm. Khi vật cách vị trí cân bằng 6 cm, tốc độ của nó bằng

A. 18,84 cm/s. B. 20,08 cm/s. C. 25,13 cm/s. D. 12,56 cm/s.

Câu 2. Một vật dao động điều hòa với tần số góc 5 rad/s. Khi vật đi qua li độ 5 cm thì nó có tốc độ là 25 cm/s. Biên độ dao động của vật là

A. 5,24cm. B. 5$\sqrt{2}$ cm. C. 5$\sqrt{3}$ cm. D. 10 cm.

Câu 3. Một vật đang dao động điều hòa với tần số góc \[10\pi \] rad/s và biên độ $\sqrt{2}$ cm. Khi vật có vận tốc 10$\sqrt{10}$ cm/s thì gia tốc của nó có độ lớn

A. 4\[m/{{s}^{2}}\] . B. 10 \[m/{{s}^{2}}\]. C. 2 \[m/{{s}^{2}}\]. D. 5 \[m/{{s}^{2}}\]

Câu 4. Một chất điểm dao động điều hòa với chu kì T. Gọi \[{{v}_{TB}}\] là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà v ≥ $\frac{\pi }{4}$ \[{{v}_{TB}}\] là

A. $\frac{T}{6}$. B. $\frac{2T}{3}$. C. $\frac{T}{3}$. D. $\frac{T}{2}$.

Câu 5. Vật dao động điều hòa với phương trình \[x\text{ }=\text{ }5cos(4\pi t\text{ }+\] $\frac{\pi }{3}$) (cm). Khi t = \[{{t}_{1}}\] thì \[{{x}_{1}}\] = -3 cm. Khi t = \[{{t}_{1}}\] + 0,25 s thì \[{{x}_{2}}\] bằng

A. 2,5 cm. B. - 2,5 cm. C. -3 cm. D. 3 cm.

Câu 6. Một con lắc lò xo dao động điều hòa với chu kì T và biên độ 5 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s² là \[\frac{T}{3}\]. Lấy \[{{\pi }^{2}}\] = 10. Tần số dao động của vật là

A. 4 Hz. B. 3 Hz. C. 1 Hz. D. 2 Hz.

Câu 7. Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là 40$\sqrt{3}$ cm/s². Biên độ dao động của chất điểm là

A. 5 cm. B. 4 cm. C. 10 cm. D. 8 cm.

Câu 8. Một chất điểm dao động điều hòa theo phương trình x = 4cos$\frac{2\pi }{3}$t (x tính bằng cm; t tính bằng s). Kể từ lúc t = 0, chất điểm đi qua vị trí có li độ x = - 2 cm lần thứ 2011 tại thời điểm

A. 3015 s. B. 6030 s. C. 3016 s. D. 6032 s.

Câu 9. Một chất điểm dao động điều hòa trên trục Ox với biên độ 10 cm, chu kì 2 s. Mốc thế năng ở vị trí cân bằng. Tốc độ trung bình của chất điểm trong khoảng thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng bằng 3 lần thế năng đến vị trí có động năng bằng $\frac{1}{3}$ lần thế năng là

A. 26,12 cm/s. B. 7,32 cm/s. C. 14,64 cm/s. D.21,96 cm/s.

Câu 10. Hai chất điểm M và N có cùng khối lượng, dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua góc tọa độ và vuông góc với Ox. Biên độ của M là 6 cm, của N là 8 cm. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M có động năng bằng thế năng, tỉ số động năng của M và động năng của N là

A. $\frac{4}{3}$. B. $\frac{3}{4}$. C. $\frac{9}{16}$. D. $\frac{16}{9}$.

Câu 11. Một chất điểm dao động điều hòa có vận tốc cực đại 60 cm/s và gia tốc cực đại là\[2\pi \text{ }m/{{s}^{2}}\] . Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu (t = 0), chất điểm có vận tốc 30 cm/s và thế năng đang tăng. Chất điểm có gia tốc bằng \[\pi \text{ }m/{{s}^{2}}\] lần đầu tiên ở thời điểm

A. 0,35 s. B. 0,15 s. C. 0,10 s. D. 0,25 s.

Câu 12. Một chất điểm dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Tốc độ trung bình của chất điểm từ thời điểm \[{{t}_{0}}\] chất điểm qua vị trí có li độ 3,5 cm theo chiều dương đến thời điểm gia tốc của chất điểm có độ lớn cực đại lần thứ 3 (kể từ \[{{t}_{0}}\]) là

A. 27,3 cm/s. B. 28,0 cm/s. C. 27,0 cm/s. D. 26,7 cm/s.

Câu 13. Một vật dao động điều hòa với chu kì T. Chọn gốc thời gian là lúc vật qua vị trí cân bằng, vận tốc của vật bằng 0 lần đầu tiên ở thời điểm

A. $\frac{T}{2}$. B. $\frac{T}{8}$. C. $\frac{T}{6}$. D. $\frac{T}{4}$.

Câu 14. Một vật nhỏ dao động theo phương trình \[x\text{ }=\text{ }5cos(\omega t\text{ }+\] $\frac{\pi }{2}$) (cm). Pha ban đầu của dao động là

A.\[\pi \] . B. $\frac{\pi }{2}$. C. $\frac{\pi }{4}$. D. $\frac{3\pi }{2}$.

Câu 15. Một chất điểm dao động theo phương trình \[x\text{ }=\text{ }6cos\omega t\] (cm). Dao động của chất điểm có biên độ là

A. 2 cm. B. 6 cm. C. 3 cm. D. 12 cm.

Câu 16. Một chất điểm dao động có phương trình \[x\text{ }=\text{ }10cos(15t\text{ }+\pi )\] (x tính bằng cm, t tính bằng s). Chất điểm này dao động với tần số góc là

A. 20 rad/s B. 10 rad/s. C. 5 rad/s. D. 15 rad/s.

Câu 17. Một chất điểm dao động điều hòa với phương trình\[x=Acos(\omega t\text{ }+\varphi )\] _; trong đó A,\[\omega \] là các hằng số dương. Pha của dao động ở thời điểm t là

A. (\[\omega \]t +\[\varphi \]). B.\[\omega \] . C.\[\varphi \] . D. \[\omega \]t.

Câu 18. Một chất điểm chuyển động tròn đều trên đường tròn tâm O bán kính A cm với tốc độ góc \[\omega \] rad/s. Hình chiếu của chất điểm lên trục Ox nằm trong mặt phẳng quỹ đạo có tốc độ cực đại là

A. $\frac{A}{\omega }$. B.\[\omega A.\] C. $\frac{\omega }{A}$. D. $\frac{1}{\omega A}$.

ĐÁP ÁN: