Đây là phần tiếp theo của bài viết “chương 2: Hàm số mũ - loga ( lý thuyết)”, các bạn có thể xem lại tại đây: https://loga.vn/bai-viet/1124/chuong-2-ham-so-mulogaly-thuyet
Vấn đề 1: TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ
Dạng toán này khá dễ, ta cần nắm vững định nghĩa và điều kiện từng loại và áp dụng.
Bảng thống kê như sau:
|
|
Điều kiện |
TXD |
|
\[{{\log }_{a}}b\] |
a > 0, a \[\ne \]1, b>0 |
|
|
\[y={{\log }_{a}}x\] |
\[a>0,a\ne
1\] |
$$D = \left( 0 \right.;\left. { + \infty } \right)$$ |
|
\[y={{a}^{x}}\] |
a>0,a \[\ne \]1 |
\[D=\mathbb{R}\] |
|
$y=\sqrt{f(x)}$ |
$$f(x) \ge 0$$ |
|
|
$y=\frac{P(x)}{Q(x)}$ |
$$Q(x) \ne 0$$ |
|
Ví dụ 1:
(ĐỀ CHÍNH THỨC 2016-2017) Tìm
tập xác định D của hàm số \[{{\log }_{5}}\frac{x-3}{x+2}\]
A. D = (-2;3) C. $$D = ( - \infty ; - 2) \cup \left( {3; + \infty } \right)$$
B. $$D = ( - \infty ; - 2) \cup \left[ {3; + \infty } \right)$$ D. \[D=R\backslash \left\{ -2 \right\}\]
Lời
giải: Điều kiện xác định của hàm số (ĐKXD) là:
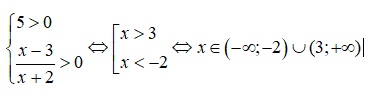
Chọn đáp án C
Ví dụ 2:
Tìm
tập xác định D của hàm số \[y=\frac{{{e}^{x}}}{{{e}^{x}}-1}\]
A.\[D=\mathbb{R}\backslash \left\{
0 \right\}\]. B. \[D=\mathbb{R}\] C. \[D=\mathbb{R}\backslash \left\{ e
\right\}\] D. \[D=\mathbb{R}\backslash
\left\{ 1 \right\}\]
Lời
giải: vì ${{e}^{x}}$ xác định với mọi x, nên ĐKXĐ của hàm số là \[{{e}^{x}}-1\ne
0\Leftrightarrow x\ne 0\]
Chọn đáp án A
Ví dụ 3:
Tìm tập xác định
D của hàm số \[y=\sqrt{{{\left( \frac{2}{3}
\right)}^{{{x}^{2}}-3x}}-\frac{9}{4}}\]
A.\[D=\left[ 0;3 \right]\] C.
B.\[D=\left[ -1;2 \right]\] D. \[D=\left[ 1;2 \right]\]
Lời
giải:
Tương tự, ĐKXĐ của hàm số trên là :
\[{{\left( \frac{2}{3} \right)}^{{{x}^{2}}-3x}}\ge
\frac{9}{4}\Leftrightarrow {{\left( \frac{2}{3} \right)}^{{{x}^{2}}-3x}}\ge
{{\left( \frac{2}{3} \right)}^{-2}}\Leftrightarrow {{x}^{2}}-3x\le -2\]
\[\Leftrightarrow {{x}^{2}}-3x+2\le 0\Leftrightarrow 1\le
x\le 2\]
Chọn đáp án D
(*) LƯU Ý TO ĐÙNG:
CÁC CÂU NÀY CÓ THỂ XỬ LÝ DỄ DÀNG BẰNG MÁY TÍNH CẦM TAY, CỤ THỂ:
ta có thể CALC các giá trị x cụ thể, nếu tại giá trị x đó, hàm số không xác định, máy tính báo lỗi. ta sẽ loại trừ đáp án đó.
Ví dụ 1:
(ĐỀ CHÍNH THỨC 2016-2017) Tìm tập xác định D của hàm số \[{{\log }_{5}}\frac{x-3}{x+2}\]
A. D = (-2;3) C. $$D = ( - \infty ; - 2) \cup \left( {3; + \infty } \right)$$
B. $$D = ( - \infty ; - 2) \cup \left[ {3; + \infty } \right)$$ D. \[D=R\backslash \left\{ -2 \right\}\]
HD:
Bước
1: nhập hàm số vào máy tính
Bước
2: CALC tại x=3 à lỗi à
loaị đáp án C và đáp án B
Bước 3: CALC tại x=0 à lỗi à loaị đáp án A à đáp án là đáp án D
Vấn đề 2. TÍNH ĐẠO HÀM
Dạng bài này cũng không quá khó, ta cần nắm vững các công thức tính đạo hàm trong chương này:
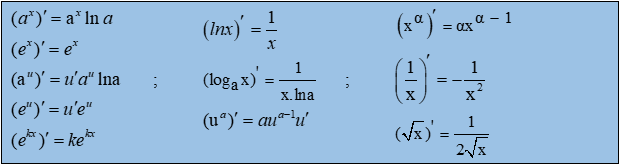
Ví dụ 1:
Tính đạo hàm của
hàm số \[y={{\left( 2{{x}^{2}}+x-1 \right)}^{\frac{2}{3}}}\]
A. \[{y}'=\frac{2(4x+1)}{3\sqrt[3]{2{{x}^{2}}+x-1}}\] C. \[{y}'=\frac{3(4x+1)}{2\sqrt[3]{{{\left( 2{{x}^{2}}+x-1
\right)}^{2}}}}\]
B. \[{y}'=\frac{3(4x+1)}{2\sqrt[3]{2{{x}^{2}}+x-1}}\] D. \[{y}'=\frac{2(4x+1)}{3\sqrt[3]{{{\left( 2{{x}^{2}}+x-1
\right)}^{2}}}}\]
Lời giải: Áp dụng công thức: \[({{u}^{a}}{)}'=a{{u}^{a-1}}{u}'\], ta có:
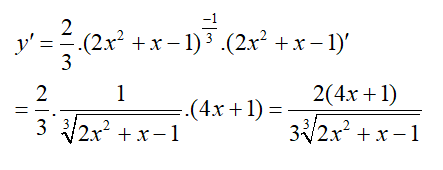
Chọn đáp án A
Ví dụ 2:
Tính đạo hàm của
hàm số\[y={{e}^{\sqrt{2x}}}\]
A.\[{y}'=\frac{{{e}^{\sqrt{2x}}}}{2\sqrt{2x}}\] B.\[{y}'=\frac{{{e}^{\sqrt{2x}}}}{\sqrt{2x}}\] C.\[{y}'=\frac{{{e}^{\sqrt{x}}}}{\sqrt{2x}}\] D.\[{y}'={{e}^{\sqrt{x}}}\]
Lời
giải: Áp dụng công thức:
\[({{e}^{u}}{)}'={u}'{{e}^{u}}\], ta có:
\[{y}'=(\sqrt{2x}{)}'.{{e}^{\sqrt{2x}}}=\frac{2}{2\sqrt{2x}}.{{e}^{\sqrt{2x}}}=\frac{{{e}^{\sqrt{2x}}}}{\sqrt{2x}}\]
Chọn đáp án B
(*)
HƯỚNG DẪN XỬ LÝ BẰNG MÁY TÍNH CẦM TAY
(-)
nguyên lý: máy tính cầm tay có hỗ trợ chức năng
tính đạo hàm tại một điểm, ta sẽ lơị dụng chức năng này để thử với đáp án bằng
cách tính đạo hàm tại một điểm x0, sau đó thay x0 vào đáp
án và so sánh.
Vd:
Tính đạo hàm của
hàm số \[y={{e}^{\sqrt{2x}}}\]
A.\[{y}'=\frac{{{e}^{\sqrt{2x}}}}{2\sqrt{2x}}\] B.\[{y}'=\frac{{{e}^{\sqrt{2x}}}}{\sqrt{2x}}\] C.\[{y}'=\frac{{{e}^{\sqrt{x}}}}{\sqrt{2x}}\] D.\[{y}'={{e}^{\sqrt{x}}}\]
Hướng
dẫn:
Bước
1: tính đạo hàm tại điểm x = 1, kết quả =2.909
Bước
2: thay x=1 vào đáp án
A A. =1.454
B B.=1.922
C C.=2.909
D D.=5.817
Dễ dàng ta thấy đáp án C là đáp án đúng.
Vấn đề 3. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Giống với chương 1, hàm số mũ và hàm số logarit cũng có dạng
toán xét tính đơn điệu.
Để xử lý dạng toán này, có nhiều cách xử lý: dùng đồ thị,
xét dấu đạo hàm, v.v.
Mình thường dựa vào đặc điểm bảng biến thiên và đồ thị hàm số
của các hàm số thường gặp. ở chương này, có một số dạng đồ thị như sau:
· · Hàm
số mũ,
0<> a>1
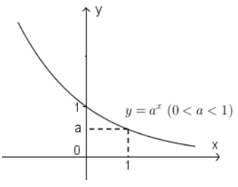
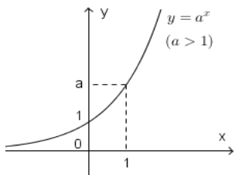
Kết
luận: từ hai đồ thị trên, dễ dàng kết luận được như sau:
o
Với 0
o Với a>1, hàm số đồng biến trên \[\mathbb{R}\].
· · Hàm số logarit, \[y={{\log }_{a}}x\]
0<> a>1
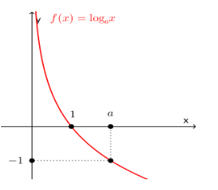
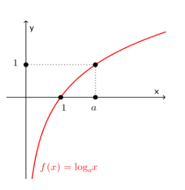
Kết luận: tương tự, ta có những
kết luận sau:
o
Với 0
o
Với a>1, hàm số đồng biến trên $$\left( {0; + \infty } \right)$$.

Kết luận:
o
Với a<0, hàm số nghịch biến trên $$\left( {0; + \infty } \right)$$.
o
Với a>0, hàm số đồng biến trên $$\left( {0; + \infty } \right)$$.
o Với a=0, hàm số là hàm hằng nên không đơn điệu trên $$\left( {0; + \infty } \right)$$.
Ví dụ 1:
Hàm số nào sau đây đồng
biến trên khoảng $$\left( {0; + \infty } \right)$$?
A. \[y={{\log
}_{0.2}}x\] B.\[y={{\log
}_{\frac{e}{3}}}x\] C.\[y=\log
x\] D.\[y={{\log
}_{\frac{\pi }{4}}}x\]
Lời
giải: Dựa vào các kết luận trên, hàm số \[y={{\log }_{a}}b\] đồng
biến khi a>1.
Chọn đáp án C
Ví dụ 2:
Hàm số nào sau
đây đồng biến trên R?
A. \[y={{\left( \frac{3}{\pi } \right)}^{x}}\] B.\[y={{\left(
\frac{\sqrt{2}+\sqrt{3}}{3} \right)}^{x}}\] C.\[y={{\left( \frac{\sqrt{3}}{3}
\right)}^{x}}\] D.\[y={{\left( \frac{\sqrt{2}}{2} \right)}^{x}}\]
Lời
giải: Dựa vào các kết luận trên, hàm số \[y={{a}^{x}}\]đồng biến trên \[\mathbb{R}\] khi a>1
Chọn đáp án B
Ví dụ 3:
Tìm tất cả số a
để hàm số \[y={{\log }_{M}}x\] vớ \[M={{a}^{2}}-4\] nghịch biến trên TXĐ.
A. \[a=2\]\[2
B. \[2<><> D. a = 2
Lời giải: hàm số đã cho nghịch biến khi cơ số 0 < M < 1, hay \[0<{{a}^{2}}-4<1\]
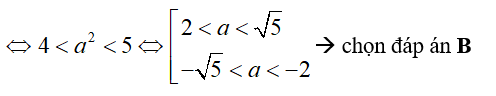
(*)
HƯỚNG DẪN XỬ LÝ BẰNG MÁY TÍNH CẦM TAY
Có rất nhiều cách giải quyết bài toán về tính đơn điệu.
trong khuôn khổ bài viết, mình hướng dẫn 1 cách khá dễ như sau:
(-) nguyên lý: ở chương 1, ta đã biết, hàm số có tính đồng biến hay nghịch biến liên quan đến dấu của đạo hàm cấp 1. Dương thì đồng biến, âm thì nghịch biến. Mặt khác, máy tính cầm tay có hỗ trợ chức năng tính đạo hàm tại một điểm. Ta sẽ áp dụng tính chất trên để thử với đáp án.
Vd:
Hàm số nào sau
đây đồng biến trên khoảng $$\left( {0; + \infty } \right)$$?
A.\[y={{\log
}_{0.2}}x\] B.\[y={{\log }_{\frac{e}{3}}}x\] C.\[y=\log x\] D.\[y={{\log
}_{\frac{\pi }{4}}}x\]
Hướng dẫn:
Bước 1: chọn x=1 thuộc
khoảng $$\left( {0; + \infty } \right)$$
Bước
2: lần lượt tính đạo tại điểm x=1 và kiểm tra dấu của kết quả.
A.
Âm (lọai)
B.
Âm (lọai)
C.
dương (nhận)
D.
Âm (lọai)
Đáp án là đáp án C
Vấn đề 4. ĐỒ THỊ
Dạng bài này rất phong phú, nhưng khi làm, chú ý những điểm sau sẽ giúp bạn làm bài dễ dàng hơn:
· · Chú ý dạng của đồ thị ( đã được đề cập ở vấn dề 3)
· · Các điểm được cho trên đồ thị
· · Các điểm lồi, lõm, điểm uốn

Lời giải: Dựa vào
hình dáng đồ thị từ trái sang phải ta thấy: x
tăng nhưng y giảm.
Suy ra hàm số tương ứng của đồ thị là hàm nghịch biến. Loại A, C.
Đồ thị
hàm số đi qua điểm có tọa độ (-1;3)
nên chỉ có D thỏa mãn.
Chọn đáp án D.

Lời
giải: Dựa vào đồ thị thấy có tiệm cận đứng
x
= -1. Loại đáp án A, B.
Đồ thị hàm số đi qua điểm có tọa độ (2;1) nên chỉ có D thỏa mãn.
Chọn đáp án D.
BÀI TẬP TỰ
LUYỆN
Câu 1: Giá trị của \[{{\log
}_{a}}\sqrt[5]{a\sqrt[3]{a\sqrt{a}}}\] với
a > 0 là:
A.\[\frac{3}{10}\] B. 4 C. \[\frac{1}{2}\] D.\[\frac{1}{4}\]
Câu 2: Chọn khẳng định sai trong các khẳng định sau:
A.\[\ln x>0\Leftrightarrow x>1\] B.\[{{\log }_{2}}x<0\Leftrightarrow
0<>
C.\[{{\log }_{\frac{1}{2}}}x<{{\log
}_{\frac{1}{2}}}y\Leftrightarrow x>y>0\] D.\[{{\log }_{\frac{1}{8}}}x>{{\log
}_{\frac{1}{8}}}y\Leftrightarrow x>y>0\]
Câu 3: Cho a là số thực dương tùy ý khác 1. Mệnh đề
nào dưới đây đúng ?
A. \[{{\log }_{2}}a={{\log }_{a}}2\]. B.
\[{{\log }_{2}}a=\frac{1}{{{\log }_{2}}a}\] C.
\[{{\log }_{2}}a=\frac{1}{{{\log }_{a}}2}\]
D. \[{{\log }_{2}}a=-{{\log }_{a}}2\]
Câu 4: Tìm tập
xác định D của hàm số \[y={{({{x}^{2}}-x-2)}^{-3}}\].
A. \[D=\mathbb{R}\] B. \[D=(0;+\infty )\]
C. \[D=(-\infty ;-1)\cup (2;+\infty )\] D. \[D=\mathbb{R}\backslash \text{
}\!\!\{\!\!\text{ }-1;2\}\]
Câu 5: Cho \[a\] là số thực dương khác 1. Tính \[I={{\log
}_{\sqrt{a}}}a\].
A. \[I=\frac{1}{2}\] B. \[I=0\] C. \[I=-2\] D. \[I=2\]
Câu
6:Cho \[a={{\log
}_{2}}5.\] Giá trị biểu thức \[{{2}^{a}}\] bằng
A. 5. B. 25. C. \[\frac{1}{5}.\] D.
32.
Câu 7: Đạo hàm của hàm số $y=\ln \left(
x+\sqrt{1+{{x}^{2}}} \right)$là:
A.$x+\sqrt{1+{{x}^{2}}}$ B.$\frac{1}{x+\sqrt{1+{{x}^{2}}}}$ C. $\frac{1}{\sqrt{1+{{x}^{2}}}}$ D.$\frac{x}{1+\sqrt{1+{{x}^{2}}}}$
Câu 8: Cho log3 = a,
log2 = b. Hãy tính \[{{\log }_{125}}30\]theo a, b
A. ${{\log
}_{125}}30=\frac{1+2a}{b}$ B. ${{\log }_{125}}30=\frac{2a}{1+b}$ C.${{\log
}_{125}}30=\frac{1+a}{1-b}$ D.${{\log
}_{125}}30=\frac{1+a}{3(1-b)}$
Câu 9: Tìm x thỏa mãn ${{\log }_{3}}x=4{{\log }_{3}}a+7{{\log }_{3}}b$ với $a>0;b>0$ta
được:
A. $x=28ab$ B.$x=4a+7b$ C.
$x={{a}^{4}}{{b}^{7}}$ D.$x=a.b$
Câu 10: Trong các hàm số sau, hàm số nào
nghịch biến trên $\mathbb{R}$?
A. $y={{\left(
\frac{2}{5} \right)}^{-x}}$ B.$y={{\left( \frac{\pi }{3} \right)}^{x}}$ C.$y={{e}^{x}}$ D. $y={{3}^{-x}}$
Câu11: Tính: K = \[\frac{{{2}^{3}}{{.2}^{-1}}+{{5}^{-3}}{{.5}^{4}}}{{{10}^{-3}}:{{10}^{-2}}-{{\left(
0,25 \right)}^{0}}}\], ta được
A.
10 B.
-10 C. 12 D. 15
Câu 12: Tính: K = \[{{\left( 0,04
\right)}^{-1,5}}-{{\left( 0,125 \right)}^{-\frac{2}{3}}}\], ta được
A.
90 B.
121 C. 120 D. 125
Câu 13: Tính: K = \[{{8}^{\frac{9}{7}}}:{{8}^{\frac{2}{7}}}-{{3}^{\frac{6}{5}}}{{.3}^{\frac{4}{5}}}\],
ta đợc
A.
2 B. 3 C.
-1 D. 4
Câu 14: Cho f(x) = \[\sqrt[3]{x}.\sqrt[6]{x}\].
Khi đó f(0,09) bằng:
A.
0,1 B. 0,2 C.
0,3 D. 0,4
Câu 15: Hàm số y = \[\frac{1}{1-\ln x}\]
có tập xác định là:
A. $$\left( {0; + \infty } \right)\backslash {\rm{ }}\left\{ e \right\}$$ B. $$\left( {0; + \infty } \right)$$ C. R D. (0; e)
Câu 16: Hàm số y = \[{{\log }_{5}}\left(
4x-{{x}^{2}} \right)\] có tập xác định là:
A.
(2; 6) B.
(0; 4) C. (0; +∞) D. R
Câu 17: Hàm số y = \[{{\log
}_{\sqrt{5}}}\frac{1}{6-x}\] có tập xác định là:
A.
(6; +∞) B. (0; +∞) C. (-∞; 6) D. R
Câu 18: Hàm số nào duới đây đồng biến
trên tập xác định của nó?
A.
y = \[{{\left( 0,5 \right)}^{x}}\] B. y = \[{{\left( \frac{2}{3}
\right)}^{x}}\] C.
y = \[{{\left( \sqrt{2} \right)}^{x}}\] D. y = \[{{\left( \frac{e}{\pi }
\right)}^{x}}\]
Câu 19: Hàm số nào duới đây thì nghịch
biến trên tập xác định của nó?
A.
y = \[{{\log }_{2}}x\] B. y = \[{{\log }_{\sqrt{3}}}x\] C. y = \[{{\log
}_{\frac{e}{\pi }}}x\] D. y = \[{{\log }_{\pi }}x\]
Câu 20: Số nào duới đây nhỏ hơn 1?
A. \[{{\left( \frac{2}{3}
\right)}^{\sqrt{2}}}\] B. \[{{\left( \sqrt{3} \right)}^{e}}\] C. \[{{\pi }^{e}}\] D. \[{{e}^{\pi }}\]
Câu 21: Số nào duới đây thì nhỏ hơn 1?
A.
\[{{\log }_{\pi }}\left( 0,7 \right)\] B. \[{{\log }_{\frac{3}{\pi }}}5\] C. \[{{\log }_{\frac{\pi }{3}}}e\] D. \[{{\log }_{e}}9\]
Câu 22: Hàm số y = \[\left(
{{x}^{2}}-2x+2 \right){{e}^{x}}\] có đạo hàm là:
A. y’
= x2ex B. y’ = -2xex C. y’ = (2x - 2)ex D. Kết quả khác
Câu 23: Cho f(x) = \[\frac{{{e}^{x}}-{{e}^{-x}}}{2}\].
Đạo hàm f’(0) bằng:
A.
4 B. 3 C. 2 D. 1
Câu 24: Cho f(x) = ln2x. Đạo
hàm f’(e) bằng:
A.
\[\frac{1}{e}\] B.
\[\frac{2}{e}\] C.
\[\frac{3}{e}\] D.
\[\frac{4}{e}\]
Câu 25: Hàm số f(x) = \[\frac{1}{x}+\frac{\ln
x}{x}\] có đạo hàm là:
A. \[-\frac{\ln x}{{{x}^{2}}}\] B.
\[\frac{\ln x}{x}\] C. \[\frac{\ln x}{{{x}^{4}}}\] D.
Kết quả khác
Câu 26: Hàm số y = \[\ln \left|
\frac{\cos x+\sin x}{\cos x-\sin x} \right|\] có đạo hàm bằng:
A. \[\frac{2}{\cos 2x}\] B.
\[\frac{2}{\sin 2x}\] C. cos2x D.
sin2x
Câu 27: Cho f(x) = \[{{\log }_{2}}\left(
{{x}^{2}}+1 \right)\]. Đạo hàm f’(1) bằng:
A. \[\frac{1}{\ln 2}\] B.
1 + ln2 C. 2 D. 4ln2
Câu 28: Cho f(x) = \[{{\lg }^{2}}x\]. Đạo
hàm f’(10) bằng:
A.
ln10 B.
\[\frac{1}{5\ln 10}\] C.
10 D. 2 + ln10
Câu 29: Cho f(x) = \[{{2}^{\frac{x-1}{x+1}}}\]. Đạo hàm f’(0) bằng:
A. 2 B.
ln2 C.
2ln2 D. Kết quả khác
Câu 30: Cho f(x) = tanx và j(x) = ln(x - 1). Tính \[\frac{f'\left(
0 \right)}{\varphi '\left( 0 \right)}\]. Đáp số của bài toán là:
A. -1 B.1 C.
2 D.
-2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
D |
C |
D |
D |
A |
C |
D |
C |
D |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
B |
B |
C |
C |
A |
B |
C |
C |
C |
A |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
A |
A |
D |
B |
A |
A |
A |
B |
B |
A |







