Chuyên đề: KHỐI ĐA DIỆN – THỂ TÍCH
Bài viết này chúng ta sẽ tìm hiểu về phương pháp và các công thức hổ trợ để tính
thể tích của các khối đa diện.
PHẦN 1: LÝ THUYẾT
I.
- Các công thức tính diện tích thường gặp:
1. Tam giác thường:
$\begin{align}
& S=\frac{1}{2}AH.BC=\frac{1}{2}ab\sin
C=\sqrt{p(p-a)(p-b)(p-c)}=\frac{abc}{4R}=pr \\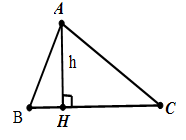
&
\\
Trong đó: p là nửa chu vi, R là bán kính đường tròn ngoại tiếp, r là bán kính đường tròn nội tiếp.
1.
Tam giác đều cạnh a:
-
Đường cao: $h=\frac{a\sqrt{3}}{2}$$$
-
$S=\frac{{{a}^{2}}\sqrt{3}}{4}$${{a}^{3}}$
Đường cao cũng là đường trung tuyến, đường phân giác, đường trung trực
Tam giác vuông
-
$S=\frac{1}{2}ab$ (a, b
là hai cạnh góc vuông)
-
Tâm đường tròn ngoại tiếp
tam giác là trung điểm của cạnh huyền.
2 Tam giác vuông cân (nửa
hình vuông)
-
$S=\frac{1}{2}{{a}^{2}}$
(2 cạnh góc vuông bằng nhau)
-
Cạnh huyền $a\sqrt{2}$
3.
Nửa tam giác đều:
-
Là tam giác vuông có một
góc bằng ${{30}^{0}}$ hoặc ${{60}^{0}}$
-
$S=\frac{{{a}^{2}}\sqrt{3}}{8}$
4.
Tam giác cân:
-
$S=\frac{1}{2}ah$ (h: đường
cao; a: cạnh đáy)
-
Đường cao hạ từ đỉnh
cũng là đường trung tuyến, đường phân giác, đường trung trực.
5.
Hình chữ nhật: $S=ab$ (a,b là các kích thước)
6.
Hình thoi: $S=\frac{1}{2}{{d}_{1}}.{{d}_{2}}$(${{d}_{1}},{{d}_{2}}$ là
hai đường chéo)
7.
Hình vuông: $S={{a}^{2}}$ Đường chéo bằng $a\sqrt{2}$.
8.
Hình bình hành: $S=ah$ (h: đường cao, a: cạnh đáy)
9. Hình thang: $S=\frac{1}{2}h$(đáy lớn + đáy bé)
I. Công thức thể tích:
1. Thể tích khối chóp:
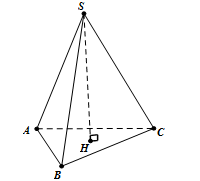
B: Diện tích đa giác đáy
1.
$V=B.h$
B: Diện tích đa giác đáy
h: Độ dài đường cao
Tỷ số thể tích: Cho khối chóp S.ABC, $A'\in SA,B'\in SB,C'\in SC$
$\frac{{{V}_{S.ABC}}}{{{V}_{S.A'B'C'}}}=\frac{SA.SB.SC}{SA'.SB'.SC'}$
2. Tính thể
tích bằng phương pháp tọa độ trong không gian:
Thể tích khối tứ diện ABCD: ${{V}_{ABCD}}=\frac{1}{6}\left|
\left[ \overrightarrow{AB};\overrightarrow{AC} \right].\overrightarrow{AD}
\right|$
Đường cao AH của tứ diện ABCD: $V=\frac{1}{3}{{S}_{BCD}}.AH\Rightarrow
AH=\frac{3V}{{{S}_{BCD}}}$
Thể tích hình hộp: ${{V}_{ABCD.A'B'C'D'}}=\left| \left[ \overrightarrow{AB},\overrightarrow{AD} \right].\overrightarrow{AA'} \right|$
PHẦN 2: BÀI TẬP MINH HỌA
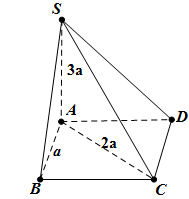$BC=\sqrt{A{{C}^{2}}-A{{B}^{2}}}=\sqrt{4{{a}^{2}}-{{a}^{2}}}=a\sqrt{3}$
Diện tích đáy: ${{S}_{ABCD}}=AB.BC={{a}^{2}}\sqrt{3}$
Thể tích khối chóp S.ABCD
là:
${{V}_{S.ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SA=\frac{1}{3}.{{a}^{2}}\sqrt{3}.3a={{a}^{3}}\sqrt{3}$
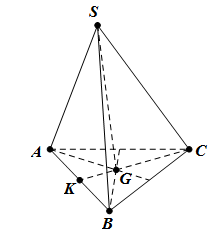${{S}_{\vartriangle
ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}$
Góc giữa SC với
đáy bằng $\widehat{SCG}={{60}^{0}}$
$CK=\frac{a\sqrt{3}}{2}\Rightarrow
CG=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$
$\Delta SGC$ vuông tại G, suy ra: $\tan {{60}^{0}}=\frac{SG}{CG}\Rightarrow
SG=CG.\tan {{60}^{0}}=\frac{a\sqrt{3}}{3}.\sqrt{3}=a$
Thể tích khối chóp S.ABC là: $V=\frac{1}{3}.{{S}_{\Delta ABC}}.SG=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.a=\frac{\sqrt{3}{{a}^{3}}}{12}$
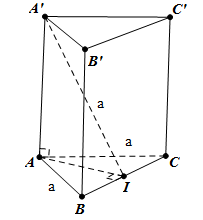
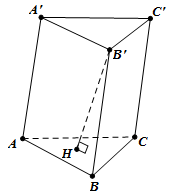
$$ $\Delta
ABC$
${{S}_{\Delta
ABCD}}=\frac{1}{2}AB.AC=\frac{1}{2}{{a}^{2}}$
$BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=a\sqrt{2}$
$$ $\Delta
A'AI$ vuông tại A:
⇒$A'A=\sqrt{A'{{I}^{2}}-A{{I}^{2}}}=\sqrt{{{a}^{2}}-\frac{{{a}^{2}}}{2}}=a$
Thể tích khối lăng trụ $ABC.A'B'C'$ là: $V={{S}_{ABC}}.A'A=\frac{1}{2}.{{a}^{2}}.a=\frac{{{a}^{3}}}{2}$
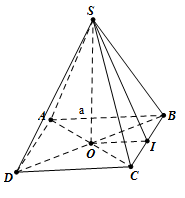
Diện
tích đáy ABCD là ${{S}_{ABCD}}={{a}^{2}}$
Góc giữa
mặt bên SBC với đáy bằng góc SIO bằng 600
Đường cao $SO=IO.\tan
{{60}^{0}}=\frac{a}{2}.\sqrt{3}=\frac{a\sqrt{3}}{2}$
Thể tích khối chóp S.ABCD là:
${{V}_{S.ABCD}}=\frac{1}{3}.{{S}_{ABCD}}.SO=\frac{1}{3}.{{a}^{2}}.\frac{a\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{3}}{6}$
PHẦN 3: BÀI TẬP TỰ LUYỆN
Câu 1: Khối đa diện đều loại $\left\{ 4;3 \right\}$có số đỉnh là:
A.4 B.6 C.8 D.10
Câu 2: Khối đa diện đều loại $\left\{ 3;4 \right\}$có số cạnh là:
A.14 B.12 C.10 D.8
Câu 3: Khối 12 mặt đều thuộc loại: A.$\left\{ 5,3 \right\}$ B.$\left\{ 3,5 \right\}$ C.$\left\{ 4,3 \right\}$ D.$\left\{
3,4 \right\}$
Câu 4: Khối lập phương là khối
đa diện loại:
A.$\left\{ 5,3 \right\}$ B.$\left\{
3,4 \right\}$ C.$\left\{ 4,3
\right\}$ D.$\left\{ 3,5 \right\}$
Câu 5: Cho hình chóp S.ABCD
có đáy ABCD là hình vuông cạnh a. Biết $SA\bot (ABCD)$và $SA=a\sqrt{3}$. Thể
tích của khối chóp S.ABCD là:
A. ${{a}^{3}}\sqrt{3}$ B.
$\frac{{{a}^{3}}}{4}$ C. $\frac{{{a}^{3}}\sqrt{3}}{3}$ D. $\frac{{{a}^{3}}\sqrt{3}}{12}$
Câu 6: Thể tích của chóp tam
giác đều có tất cả các cạnh đếu bằng a là:
A.${{a}^{3}}\frac{\sqrt{2}}{12}$ B.${{a}^{3}}\frac{\sqrt{2}}{4}$ C.${{a}^{3}}\frac{\sqrt{2}}{6}$ D.${{a}^{3}}\frac{\sqrt{2}}{2}$
Câu 7: Cho hình lăng trụ đều
ABC.A’B’C’ có cạnh đáy bằng 2a. Thể tích của khối lăng trụ là:
A. ${{a}^{3}}\frac{\sqrt{3}}{2}$ B.${{a}^{3}}\frac{\sqrt{3}}{6}$ C. ${{a}^{3}}$ D. $\frac{{{a}^{3}}}{3}$
Câu 8: Cho hình chóp S.ABC có
đáy ABC là tam giác vuông tại B, biết $AB=a$,$AC=2a$.$SA\bot (ABC)$ và $SA=a\sqrt{3}$.
Thể tích khối chóp S.ABC là:
A.$\frac{3{{a}^{3}}}{4}$ B.
$\frac{{{a}^{3}}}{4}$ C.$\frac{3{{a}^{3}}}{8}$ D. $\frac{{{a}^{3}}}{2}$
Câu 9: Cho khối lăng trụ
ABC.A’B’C’ có thể tích là V, thể tích khối chóp C’.ABC là:
A.$2V$ $$ B. $\frac{1}{2}V$ C. $\frac{1}{3}V$ D.$\frac{1}{6}V$
Câu 10: Cho khối chóp S.ABC,
trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ sao cho $SA'=\frac{1}{2}SA$,
$SB'=\frac{1}{3}SB$, $SC'=\frac{1}{4}SC$. Gọi V, V’ lần lượt là thể tích của
các khối chóp S.ABC và S.A’B’C’. Khi đó tỷ số $\frac{V'}{V}$ là:
A.12 B. $\frac{1}{12}$ C.24 D. $\frac{1}{24}$
Câu 11: Cho hình chóp S.ABCD
có đáy ABCD là hình thoi tâm O cạnh a, góc $\widehat{BAC}={{60}^{0}}$, $SO\bot
(ABCD)$ và $SO=\frac{3a}{4}$. Khi đó thể tích khối chóp là:
A.$\frac{{{a}^{3}}\sqrt{3}}{8}$ B.$\frac{{{a}^{2}}\sqrt{3}}{8}$ C.$\frac{{{a}^{3}}\sqrt{2}}{4}$ D.$\frac{{{a}^{3}}\sqrt{3}}{4}$
Câu 12: Hình chóp tứ giác
S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a; các cạnh bên đều có độ dài
bằng 3a. Thể tích hình chóp S.ABCD là:
A.$\frac{{{a}^{3}}\sqrt{31}}{3}$ B. $\frac{{{a}^{3}}}{3}$ C.$\frac{{{a}^{3}}\sqrt{31}}{9}$ D.$\frac{{{a}^{3}}\sqrt{6}}{9}$
Câu 13: Cho hình chóp S.ABCD có
đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và nằm trong mặt phẳng
vuông góc với (ABCD). Thể tích của khối chóp S.ABCD là:
A.$\frac{{{a}^{3}}\sqrt{3}}{6}$ B.$\frac{{{a}^{3}}\sqrt{3}}{2}$ C.$\frac{{{a}^{3}}}{3}$ D.${{a}^{3}}$
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
C |
B |
A |
C |
C |
A |
A |
B |
C |
D |
A |
A |
A |
