𝔅1. KHÁI NIỆM CƠ BẢN
1. Mặt nón tròn xoay
1.1. Định nghĩa mặt nón
Trong mặt phẳng (P) cho 2 đường thẳng d và ∆ cắt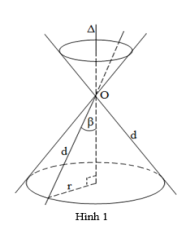 
nhau tại O và tạo thành góc β với 0O < β < 90O .
Khi quay mặt phẳng (P) xung quanh ∆ thì đường thẳng d sinh ra một mặt tròn xoay gọi là mặt nón tròn xoay đỉnh O ( gọi tắt mặt nón )
Đường thẳng ∆ gọi là trục
Đường thẳng d gọi là đường sinh
Góc 2β gọi là góc ở đỉnh của mặt nón.
1.2. Hình nón tròn xoay
a) Cho ∆OIM vuông tại I . Khi quay tam giác đó quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón tròn xoay ( gọi tắt là hình nón )
Hình tròn ( I; r) gọi là mặt đáy hình nón
Điểm O được gọi là đỉnh hình nón
OI là chiều cao hình nón
OM là đường sinh của hình nón
b) Khối nón tròn xoay
Còn gọi là khối nón, là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó.
Những điểm không thuộc khối nón gọi là điểm ngoài khối nón
Những điểm thuộc khối nón nhưng không thuộc hình nón ứng với khối nón ấy gọi là điểm trong khối nón
Đỉnh, mặt đáy, đường sinh của một hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.
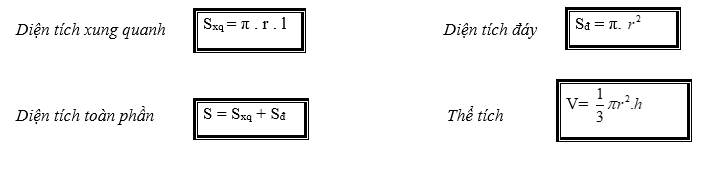
1.3. Một số công thức cần nắm
Cho hình nón có chiều cao h, bán kính đáy r và đường sinh l thì ta có:
2. Mặt trụ tròn xoay
2.1. Định nghĩa
Trong mp (P) cho 2 đường thẳng ∆ và ℓ song song với nhau, cách nhau một khoảng bằng r . Khi quay mp (P) xung quanh ∆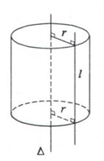
thì đường thẳng ℓ sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay ( gọi tắt là mặt trụ )
Đường thẳng ∆ gọi là trục , đường thẳng ℓ là đường sinh của mặt trụ đó.
2.2. Hình trụ tròn xoay và khối trụ tròn xoay
a) Xét hình chữ nhật ABCD. Khi quay hình đó quanh đường thẳng chứa một cạnh ( chẳng hạn cạnh AB ) thì đường gấp khúc ADCB tạo thành một hình trụ được gọi là hình trụ tròn xoay ( gọi tắt hình trụ)
Khi quay quanh AB, hai cạnh AD và BC sẽ vạch ra hai đường tròn bằng nhau, gọi là hai đáy của hình trụ
CD gọi là đường sinh hình trụ
AB là chiều cao hình trụ
b) Khối trụ tròn xoay
Là phần không gian được giới hạn bởi một hình trụ tròn xoay ( kể cả hình trụ đó).
Khối trụ tròn xoay được gọi tắt là khối trụ.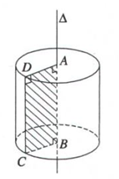
Ta gọi mặt đáy , chiều cao, đường sinh của một hình trụ theo thứ tự là mặt đáy, chiều cao, đường sinh
của khối trụ tương ứng.
2.3. Một số công thức cần nắm
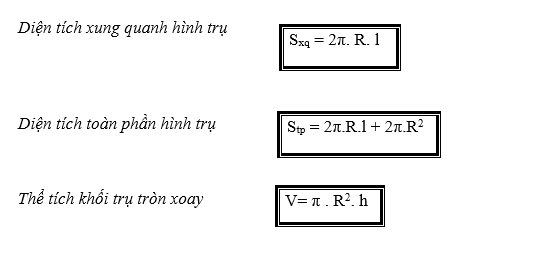
3. Mặt cầu
3.1. Định nghĩa
Tập hợp những điểm M trong không gian cách điểm O cố định
một khoảng không đổi bằng R ( R>0 ) được gọi là mặt cầu tâm O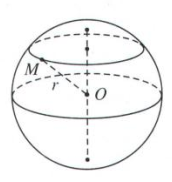 
bán kính R
Kí kiệu S(O ; R) = {M \ OM = R}
3.2. Các thuật ngữ
- Bán kính : A ϵ S(O;R) => OA là một bán kính của mặt cầu
- Đường kính: A, B ϵ S(O;R) và O, A, B thẳng hàng => đoạn thẳng AB
là một đường kính của mặt cầu
- Điểm trong : Nếu OE < R=> E là điểm trong của mặt cầu
- Điểm ngoài : Nếu OF > R => F là điểm ngoài của mặt cầu
- Mp qua tâm mặt cầu gọi là mặt kính. Giao tuyến của mặt cầu và mặt kính là đường
tròn C(O;R) – gọi là tâm đường tròn lớn
- Khối cầu S(O;R) hoặc hình cầu S(O;R) là tập hợp các điểm thuộc mặt cầu S(O;R) và
các điểm nằm trong mặt cầu đó
Ta có thể định nghĩa : Khối cầu S(O;R) = {M| OM ≤ R}
3.3. Giao của mặt cầu và mặt phẳng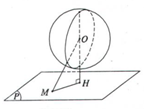 
Kí hiệu d(O, (P)) = OH là khoảng cách từ tâm mặt cầu đến mp(P).
a) Trường hợp h > R
Mặt phẳng không cắt mặt cầu
b) Trường hợp h = R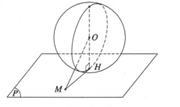
Mặt phẳng tiếp xúc với mặt cầu
Điểm H gọi là tiếp điểm của mp và mặt cầu
Mặt phẳng (P) gọi là tiếp diện của mặt cầu
c) Trường hợp h < R
Mặt phẳng cắt mặt cầu theo đường tròn tâm H, bán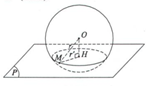
kính \[r=\sqrt{{{R}^{2}}-{{h}^{2}}}\]
3.4. Giao của mặt cầu với đường thẳng. Tiếp tuyến của mặt cầu
Trường hợp này tương tự như trường hợp 3.3 kể trên, các bạn có thể xem qua SGK để nắm rõ
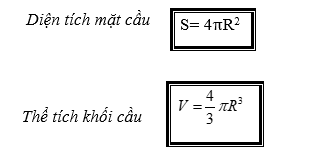
3.5. Một số công thức cần nắm
𝔅2. VÍ DỤ MINH HỌA VÀ BÀI TẬP
Bài tập tự luyện
1. Cho hình nón có bán kính đáy là 4a, chiều cao là 3a. Diện tích toàn phần hình nón là
A. \[38\pi {{a}^{2}}\] B. \[32\pi {{a}^{2}}\] C. \[36\pi {{a}^{2}}\] D. \[30\pi {{a}^{2}}\]
2. Cho hình chóp ∆ đều S.ABC có cạnh đáy bằng a và góc giữa một cạnh bên và đáy bằng \[{{60}^{o}}\] , diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ∆ABC là
A. \[\frac{13\pi {{a}^{2}}}{12}\] B. \[\frac{\pi {{a}^{2}}\sqrt{13}}{12}\] C. \[\frac{\pi {{a}^{2}}\sqrt{13}}{\sqrt{12}}\] D. \[\frac{\pi {{a}^{2}}}{12}\]
3. Cho hình chóp ∆ đều S.ABC có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng \[{{60}^{o}}\] , diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ∆ABC là
A. \[\frac{\pi {{a}^{2}}}{4}\] B. \[\frac{\pi {{a}^{2}}}{6}\] C. \[\frac{\pi {{a}^{2}}}{3}\] D. \[\frac{5\pi {{a}^{2}}}{6}\]
4. Hình trụ (T) được sinh ra khi qua hình chữ nhật ABCD quanh cạnh AB. Biết AC= \[a\sqrt{2}\] và ACB= \[{{45}^{o}}\]. Tính diện tích toàn phần của hình trụ (T) là
A. \[4\pi {{a}^{2}}\] B. \[10\pi {{a}^{2}}\] C. \[12\pi {{a}^{2}}\] D. \[8\pi {{a}^{2}}\]
5. Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a. Tam giác ABC vuông tại A có BC = \[2a\sqrt{3}\]. Thể tích hình trụ ngoại tiếp khối lăng trụ này là
A. \[6\pi {{a}^{3}}\] B. \[4\pi {{a}^{3}}\] C. \[2\pi {{a}^{3}}\] D. \[8\pi {{a}^{3}}\]
6. Cho hình chữ nhật ABCD có cạnh AB= 2a , AD = 4a. Gọi M,N lần lượt là trung điểm của AB và CD. Quay hình chữ nhật ABCD quanh trục MN ta được khối trụ tròn xoay. Thể tích khối trụ là
A. \[4\pi {{a}^{3}}\] B. \[2\pi {{a}^{3}}\] C. \[\pi {{a}^{3}}\] D. \[5\pi {{a}^{3}}\]
7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=2a và vuông góc với (ABCD). Thể tích khối cầu ngoại tiếp khối chóp S.ABCD là
A. \[\frac{\pi {{a}^{3}}}{\sqrt{6}}\] B. \[\pi {{a}^{3}}\sqrt{6}\] C. \[\frac{\pi {{a}^{3}}4\sqrt{6}}{3}\] D. \[\frac{\pi {{a}^{3}}\sqrt{6}}{3}\]
8. Cho hình chóp S.ABC có SA= 2a và SA vuông góc (ABC). Tam giác ABC vuông cân tại B, AB=\[a\sqrt{2}\]. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là
A. 2a B. \[\frac{a\sqrt{2}}{2}\] C. \[2a\sqrt{2}\] D. \[a\sqrt{2}\]
9. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2 và cạnh bên bằng \[2\sqrt{3}\]. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC
A. \[\frac{3\sqrt{6}}{2}\] B. \[\frac{3\sqrt{6}}{4}\] C. \[\frac{3\sqrt{6}}{6}\] D. \[\frac{3\sqrt{6}}{8}\]
