Chuyên đề: Tiếp tuyến của đồ thị hàm số
A. Lý thuyết
I. Định nghĩa
- Cho (C) là đồ thị hàm số y=f(x) và điểm $M\left( {{x}_{0}};f\left( {{x}_{0}} \right) \right)\in \left( C \right)$. Tiếp tuyến với (C) tại điểm M có phương trình là: \[y={{f}^{,}}({{x}_{0}})(x-{{x}_{0}})+f({{x}_{0}})\].
- Chú ý: Nguyên tắc chung để lập được phương trình tiếp tuyến là phải tìm được giá trị \[{{x}_{0}}\].
II. Tính nhanh đạo hàm tại một điểm bằng VINACAL (các máy khác tương tự)
- Ta sử dụng phím
 (SHIFT\[\to \]TÍCH PHÂN)
(SHIFT\[\to \]TÍCH PHÂN) - Ví dụ: Tính đạo hàm tại x=1 của hàm số \[y=\sqrt{2x}\] ta làm như sau:
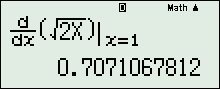
- Chú ý: Trong các bài tập minh họa dưới đây phần tính đạo hàm tại một giá trị dành cho bạn đọc.
B. Bài tập
I. Bài tập minh họa:
Dạng 1: Viết phương trình tiếp tuyến khi biết tiếp điểm
|
Câu 1: Phương trình tiếp tuyến của đồ thị (C): \[y={{x}^{3}}+2{{x}^{2}}\]tại điểm M(1;3) là A. y=7x+4 B. y=7x-4 C. y=-7x+4 D. y=-7x-4
|
Lời giải: Chọn B.
Ta có: y’(1)=7. Áp dụng công thức: \[y={{f}^{'}}({{x}_{0}})(x-{{x}_{0}})+f({{x}_{0}})\]. Nên phương trình tiếp tuyến là: y=7(x-1)+3\[\Leftrightarrow \]y=7x-4.
|
Câu 2: Cho điểm M thuộc đồ thị (C): \[y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}\] có hoành độ \[{{x}_{0}}>0\] và \[y''\left( {{x}_{0}} \right)=-1\]. Phương trình tiếp tuyến của (C) tại điểm M là A. \[y=-3x+\frac{5}{4}\] B. \[y=3x+\frac{5}{4}\] C. \[y=3x-\frac{19}{4}\] D. \[y=-3x-\frac{19}{4}\]
|
Lời giải: Chọn A.
\[y'={{x}^{3}}-4x\Rightarrow y''=3{{x}^{2}}-4\]. Mà y’’=-1\[\Rightarrow 3{{x}^{2}}-4=-1\Leftrightarrow x=1\] (\[{{x}_{0}}>0\]).
Vậy áp dụng công thức: \[y={{f}^{'}}({{x}_{0}})(x-{{x}_{0}})+f({{x}_{0}})\]\[\Rightarrow y=f'\left( 1 \right)\left( x-1 \right)+f\left( 1 \right)\Leftrightarrow y=-3\left( x-1 \right)-\frac{7}{4}\Leftrightarrow y=-3x+\frac{5}{4}\].
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc k
|
Câu 1: Phương trình tiếp tuyến của đồ thị hàm số (C) : \[y={{x}^{3}}-3x+2\] có hệ số góc bằng 9 là A. y=9x-18; y=9x+22 B. y=9x-14; y=9x+18 C. y=9x+18; y=9x+22 D. y=9x-14; y=9x-18
|
Lời giải: Chọn B.
\[y'=3{{x}^{2}}-3=9\Leftrightarrow x=\pm 2\]. Vậy có hai tiếp tuyến tại hai điểm M(2;4), N(-2;0).
Phương trình tiếp tuyến tại M: y=9(x-2)+4\[\Leftrightarrow \]y=9x-14.
Phương trình tiếp tuyến tại N: y=9(x+2)\[\Leftrightarrow y=9x+18\].
|
Câu 2: Tiếp tuyến của đồ thị (C): \[y=\frac{2x+1}{x+2}\] song song với đường thẳng \[\Delta :3x-y+2=0\] có phương trình là A. y=3x-4 B. y=3x+2 C. y=3x+14 D. y=3x+4
|
Lời giải: Chọn C.
\[y'=\frac{3}{{{\left( x+2 \right)}^{2}}}\]. Ta có: \[\Delta :3x-y+2=0\Leftrightarrow y=3x+2\]. Vì tiếp tuyến song song \[\Delta \]. Nên y’=3.
\[\Leftrightarrow \frac{3}{{{\left( x+2 \right)}^{2}}}=3\Leftrightarrow {{\left( x+2 \right)}^{2}}=1\Leftrightarrow \].png) .
.
Vậy có 2 tiếp tuyến tại M(-1;-1) và N(-3;5).
Phương trình tiếp tuyến tại M: y=3(x+1)-1=3x+2 (loại vì trùng với \[\Delta \]).
Phương trình tiếp tuyến tại N: y=3(x+3)+5=3x+14.
Vậy tiếp tuyến song song \[\Delta \] là y=3x+14.
Dạng 3: Viết phương trình tiếp tuyến đi qua một điểm cho trước
|
Câu 1: Tiếp tuyến của đồ thị hàm số \[y=\frac{2x-1}{x+1}\] đi qua điểm A(-1;4) có phương trình là A. \[y=\frac{1}{3}x+\frac{13}{3}\] B. \[y=\frac{1}{3}x+\frac{1}{3}\] C. \[y=\frac{1}{3}x+4\] D. \[y=\frac{1}{3}x+1\]
|
Lời giải: Chọn A.
Phương trình tiếp tuyến là \[y=f'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+{{y}_{0}}\]. Vì tiếp tuyến qua điểm A(-1;4) nên \[4=\frac{3}{{{\left( {{x}_{0}}+1 \right)}^{2}}}\left( -1-{{x}_{0}} \right)+\frac{2{{x}_{0}}-1}{{{x}_{0}}+1}\Leftrightarrow {{x}_{0}}=-4\]. Vậy tiếp tuyến qua điểm A(-1;4) có tiếp điểm là \[M\left( -4;3 \right)\].
Vậy phương trình tiếp tuyến tại \[M\left( -4;3 \right)\] là \[y=y\left( -4 \right)\left( x+4 \right)+3\Leftrightarrow y=\frac{1}{3}\left( x+4 \right)+3\Leftrightarrow y=\frac{1}{3}x+\frac{13}{3}\].
|
Câu 2: Tiếp tuyến của đồ thị hàm số \[y=-4{{x}^{3}}+3x+1\] đi qua điểm A(-1;2) có phương trình là A. y= -9x+7; y=-x+2 B. y=-9x-11; y=-x+2 C. y=-9x+11; y=2 D. y=-9x-7; y=2
|
Lời giải: Chọn D.
Phương trình tiếp tuyến là \[y=f'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+{{y}_{0}}\]. Vì tiếp tuyến qua điểm A(-1;2) nên \[2=\left( -12x_{0}^{2}+3 \right)\left( -1-{{x}_{0}} \right)-4x_{0}^{3}+3{{x}_{0}}+1\Leftrightarrow 8x_{0}^{3}+12x_{0}^{2}-4=0\Leftrightarrow \].png) .
.
Vậy có hai tiếp tuyến qua điểm A(-1;2) tại các tiếp điểm \[M\left( \frac{1}{2};2 \right)\] và N(-1;2).
Phương trình tiếp tuyến tại \[M\left( \frac{1}{2};2 \right)\]: \[y=y'\left( \frac{1}{2} \right)\left( x-\frac{1}{2} \right)+2\Leftrightarrow y=2\].
Phương trình tiếp tuyến tại N(-1;2): \[y=y\left( -1 \right)\left( x+1 \right)+2\Leftrightarrow y=-9\left( x+1 \right)+2\Leftrightarrow y=-9x-7\].
Dạng 4: Một số bài toán chứa tham số
|
Câu 1: Cho hàm số \[y=\frac{x+2}{2x+3}\] có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng A. 1 B. 2 C. 3 D. -3
|
Lời giải: Chọn D.
Đường thẳng d: y=kx+m cắt trục hoành tại \[A\left( -\frac{m}{k};0 \right)\], trục tung tại B(0;m).
Vì tam giác OAB cân tại O nên: \[\left| -\frac{m}{k} \right|=\left| m \right|\Leftrightarrow \left| k \right|=1\Leftrightarrow k=\pm 1\]. Vì \[k=y'=\frac{-1}{{{\left( 2x+3 \right)}^{2}}}<0\]. Nên k=1 loại.
\[k=-1\Leftrightarrow \frac{-1}{{{\left( 2x+3 \right)}^{2}}}=-1\Leftrightarrow 2x+3=\pm 1\Leftrightarrow \].png) .
.
Tại tiếp điểm E(-1;1) phương trình tiếp tuyến là: y=-(x+1)+1=-x.
Tại tiếp điểm F(-2;0) phương trình tiếp tuyến là:y=-(x+2)=-x-2
Vậy k=-1; m=-2. Nên k+m=-3.
|
Câu 2: Tìm tập hợp tất cả các giá trị tham số thực m để đồ thị (C) của hàm số \[y=\frac{2x+3}{x+1}\] cắt đường thẳng \[y=2x+{{m}^{2}}\] tại hai điểm phân biệt mà hai tiếp tuyến của (C) tại hai điểm đó song song với nhau. A. {2} B. {-1;-1} C. {1;-1} D. {-2;2}
|
Lời giải: Chọn D.
Xét phương trình hoành độ giao điểm: \[\frac{2x+3}{x+1}=2x+{{m}^{2}}\Rightarrow 2{{x}^{2}}+{{m}^{2}}x+{{m}^{2}}-1=0\] có hai nghiệm phân biệt khác -1. Khi đó hoành độ tiếp điểm là nghiệm \[{{x}_{1}};{{x}_{2}}\] của phương trình trên.
Vì tiếp tuyến tại hai điểm song song nên \[{{k}_{1}}={{k}_{2}}\Leftrightarrow \frac{-1}{{{\left( {{x}_{1}}+1 \right)}^{2}}}=\frac{-1}{{{\left( {{x}_{2}}+1 \right)}^{2}}}\Leftrightarrow {{\left( {{x}_{1}}+1 \right)}^{2}}={{\left( {{x}_{2}}+1 \right)}^{2}}\Leftrightarrow \].png) .
.
Vì \[{{x}_{1}}\ne {{x}_{2}}\]. Nên \[{{x}_{1}}+{{x}_{2}}=-2\Leftrightarrow -\frac{{{m}^{2}}}{2}=-2\Leftrightarrow m=\pm 2\] . Thử lại m vào phương trình hoành độ giao điểm thấy thỏa mãn đề bài. Vậy C là đáp án đúng.
II. Bài tập tự luyện
Câu 1: Tiếp tuyến của (C) :\[y={{x}^{4}}-2{{x}^{2}}\] tại điểm có hoành độ bằng -2 có phương trình là
A. y=-24x-40 B. y=-24x+40 C. y=24x-40 D. y=24x+40
Câu 2: Tiếp tuyến của (C): \[y=\frac{2x-2}{x-2}\] tại điểm có tung độ bằng 3 có phương trình là
A. \[y=\frac{1}{2}x-5\] B. \[y=\frac{1}{2}x+5\] C. \[y=-\frac{1}{2}x+5\] D. \[y=-\frac{1}{2}x-5\]
Câu 3: Tiếp tuyến của đồ thị \[y=-{{x}^{4}}-{{x}^{2}}+6\] vuông góc với đường thẳng \[\Delta :y=\frac{1}{6}x-1\] có phương trình là
A. y=-6x-2 B. y=-6x+2 C. y=-6x+10 D. y=-6x-10
Câu 4: Đồ thị hàm số \[y={{x}^{4}}-2{{x}^{2}}+1\] có bao nhiêu tiếp tuyến song song với trục hoành
A. 1 B. 2 C. 3 D. 4
Câu 5: Cho hàm số \[y={{x}^{3}}-6x+2\]. Hỏi có bao nhiêu tiếp tuyến của đồ thị hàm số qua A(1;-3)
A. 3 B. 2 C. 0 D. 1
Câu 6: Có bao nhiêu tiếp tuyến của đồ thị \[y=\frac{2x-1}{x-1}\] cách đều hai điểm A(-2;4) và B(4;-2)
A. 1 B. 2 C. 3 D. 5
Câu 7: Cho hàm số \[y=\frac{x-1}{x-2}\] có đồ thị (C). Gọi I là giao điểm hai đường tiệm cận của (C). Tiếp tuyến d của (C) tại điểm M thõa mãn \[IM\bot d\] có phương trình là
A. y=-x+1; y=-x-5 B. y=-x+1; y=-x+5
C. y=-x-1; y=-x-5 D. y=-x-1; y=-x+5
Câu 8: Cho hàm số \[y=\frac{-x+1}{2x+1}\] có đồ thị (C). Đường thẳng d; y=kx+m là tiếp tuyến của (C) và tiếp tuyến này đi qua giao điểm của đường tiệm cận và trục hoành Ox. Tỉ số k:m bằng
A. 2 B. -2 C. 1 D. -1
Câu 9: Cho hàm số \[y=\frac{x+b}{ax-2}\] có đồ thị hàm số (C). Biết a, b là các giá trị thực sao cho tiếp tuyến của (C) tại điểm M(1;-2) song song với đường thẳng d: 3x+y-4=0. Tính a+b.
A. 0 B. -1 C. 2 D. 1
Câu 10: Cho hàm số \[y=\frac{x+1}{x-2}\] có đồ thị (C). Gọi d là khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của (C). Tìm d.
A. \[\frac{\sqrt{2}}{2}\] B. \[\sqrt{5}\] C. \[\sqrt{3}\] D. \[\sqrt{6}\]
Đáp án bài tập tự luyện:
.png)







