Đa thức một biến

Đa thức một biến

I.Lý thuyết:

1. Đa thức một biến

Đa thức một biến là tổng của những đơn thức của cùng một biến.

Lưu ý: Một số được coi là đa thức một biến .

2. Biến của đa thức một biến

Bậc của đa thức một biến khác đa thức không (đã thu gọn) là số mũ lớn nhất của biến có trong đa thức đó.

3. Hệ số, giá trị của một đa thức

a) Hệ số của đa thức

Hệ số cao nhất là hệ số của số hạng có bậc cao nhất

Hệ số tự do là số hạng không chứa biến.

b) Giá trị của đa thức f(x) tại x = a được kí hiệu là f(a) có được bằng cách thay x = a vào đa thức f(x) rồi thu gọn lại.

II. Bài tập vận dụng:

Bài 1: Tính A(5), B(-2), với A(y) và B(x) với các đa thức sau.

a) A(y) = 7y² – 3y + \[\frac{1}{2}\]

b) B(x) = 2x⁵ – 3x + 7x³ + 4x⁵ + \[\frac{1}{2}\]

Hướng dẫn

- Ta có: A(y) = 7y² – 3y + \[\frac{1}{2}\]

A(5) là giá trị của đa thức A(y) tại y = 5

⇒ A(5) = 7. 5² – 3.5 + \[\frac{1}{2}\]

= 7. 25 – 15 + \[\frac{1}{2}\] = 175 – 15 + \[\frac{1}{2}\]

= 160 + \[\frac{1}{2}\] = 160\[\frac{1}{2}\]

Và: B(x) = 2x⁵ – 3x + 7x³ + 4x⁵ + \[\frac{1}{2}\]

Trước hết, ta rút gọn B:

B(x) = 2x⁵ – 3x + 7x³ + 4x⁵ + \[\frac{1}{2}\]

B(x) = (2x⁵+ 4x⁵) – 3x + 7x³ + \[\frac{1}{2}\]

B(x) = 6x⁵ – 3x + 7x³ + \[\frac{1}{2}\]

(-2) là giá trị của đa thức B(x) tại x = -2

⇒ B(-2) = 6. (-2)⁵ – 3.(-2) + 7 .(-2)³ + \[\frac{1}{2}\]

= 6. (-32) – (-6) + 7. (-8) + \[\frac{1}{2}\]

= - 192 + 6 – 56 + \[\frac{1}{2}\] = - (192 – 6 + 56) + \[\frac{1}{2}\]

= - 242 + \[\frac{1}{2}\] = (- 484)/2 + \[\frac{1}{2}\]

= (-484 + 1)/2 = (-483)/2

Bài 2: Tìm bậc của đa thức A(y), B(x) nêu trên.

Hướng dẫn:

- Ta có: A(y) = 7y² – 3y + \[\frac{1}{2}\]

Đa thức A(y) có 3 hạng tử là:

7y² có bậc 2, - 3y có bậc 1 ,\[\frac{1}{2}\] có bậc 0

Mà bậc của đa thức là bậc của hạng tử có bậc cao nhất

Hạng tử có bậc cao nhất là 7y² có bậc 2

⇒ Bậc của đa thức A(y) là 2

- Ta có: B(x) = 2x⁵ – 3x + 7x³ + 4x⁵ + \[\frac{1}{2}\] = 6x⁵ – 3x + 7x³ + \[\frac{1}{2}\]

Sau khi rút gọn, đa thức B(x) có 4 hạng tử là:

6x⁵ có bậc 5, – 3x có bậc 1

7x³ có bậc 3 ,\[\frac{1}{2}\] có bậc 0

Mà bậc của đa thức là bậc của hạng tử có bậc cao nhất

Hạng tử có bậc cao nhất là 6x⁵ có bậc 5 ⇒ Bậc của đa thức B(x) là 5

Bài 3: Hãy sắp xếp các hạng tử của mỗi đa thức sau theo lũy thừa giảm dần của biến:

Q(x) = 4x³ – 2x + 5² - 2x³ + 1 - 2x³

R(x) = -2 + 2x⁴+ 2x - 3x⁴ – 10 + x⁴

Hướng dẫn

Trước hết, ta rút gọn các đa thức:

- Q(x) = 4x³ – 2x + 5² - 2x³ + 1 - 2x³

Q(x) = (4x³- 2x³- 2x³) – 2x + 5² + 1

Q(x) = 0 – 2x + 5² + 1

Q(x) = – 2x + 5² + 1

- R(x) = - 2 + 2x⁴ + 2x - 3x⁴ – 10 + x⁴

R(x) = - x² + (2x⁴- 3x⁴+ x⁴) + 2x – 10

R(x) = - x² + 0 + 2x – 10

R(x) = - x² + 2x – 10

Sắp xếp các hạng tử của đa thức sau theo lũy thừa giảm dần của biến ta có:

Q(x) = 5² – 2x + 1

R(x) = - x² + 2x – 10

Bài 4: Cho đa thức Q(x) = x² + 2x⁴ + 4x³ – 5x⁶ + 3x² – 4x – 1

a) Sắp xếp các hạng tử của Q(x) theo lũy thừa giảm của biến.

b) Chỉ ra các hệ số khác 0 của Q(x).

Hướng dẫn:

a) Thu gọn Q(x) = 4x² + 2x⁴ + 4x³ – 5x⁶ – 4x – 1

Sắp xếp theo lũy thừa giảm dần của biến:

Q(x) = – 5x⁶ + 2x⁴ + 4x³ + 4x² – 4x – 1

b) Hệ số lũy thừa bậc 6 là – 5

Hệ số lũy thừa bậc 4 là 2

Hệ số lũy thừa bậc 3 là 4

Hệ số lũy thừa bậc 2 là 4

Hệ số lũy thừa bậc 1 là –4

Hệ số lũy thừa bậc 0 là –1

Bài 5: Viết một đa thức một biến có hai hạng tử mà hệ số cao nhất là 5, hệ số tự do là -1.

Hướng dẫn

Có vô số đa thức thỏa mãn điều kiện trên, đó là:

Đa thức bậc nhất: 5x - 1

Đa thức bậc hai: 5x² - 1

Đa thức bậc ba: 5x³ - 1

Đa thức bậc bốn: 5x⁴ - 1

...........................

Tổng quát: Đa thức bậc n (n là số tự nhiên): 5xⁿ - 1

III.Bài tập tự luyện:

Bài 1: Cho đa thức f(x) = 2x – 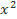+ 2|x + 1|.
Thu gọn đa thức f(x).
Tính giá trị của f(x) khi x = –3/2.
Bài 2: Cho đa thức f(x) = 2x – 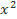+ 2|x + 1|.
Thu gọn đa thức f(x).
Tính giá trị của f(x) khi x = –3/2.

Bài 3: a) Cho đa thức f(x) = 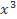+ 2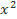 + ax + 1. Tìm a biết rằng f(x) có nghiệm là –2.
b) Biết đa thức f(x) = 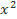+ bx + c có hai nghiệm là 1 và 2. Hãy tìm b và c.

Bài 4: Cho đa thức f(x) = a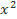 + bx + c. Tìm a, b, c biết rằng f(0) = 2 và f(x) có hai nghiệm là 1 và –1.

Bài 5: Cho đa thức bậc hai: f(x) = a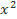 + bx + c, trong đó a, b, c là những hằng số.
Biết a + b + c = 0. Chứng minh f(x) có một nghiệm là x = 1, áp dụng để tìm các nghiệm của đa thức f(x) = 8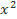 – 6x – 2.

Biết a – b + c = 0. Chứng minh f(x) có một nghiệm là x = –1, áp dụng để tìm các nghiệm của đa thức f(x) = 7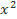 + 11x + 4.

Bài 6: a) Cho đa thức f(x) = ax + b (a ≠ 0). Chứng minh rằng nếu có hai số 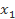, 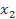là hai nghiệm của đa thức f(x) thì = .
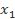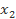b) Chứng minh rằng nếu đa thức f(x) = ax + b có hai nghiệm 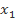, 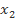khác nhau thì f(x) là đa thức 0.

Bài 7: Cho đa thức f(x) = 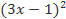– ( – 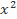4) – (8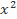+ 2x – 3) và g(x) = a 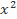+ bx – 4.
Thu gọn đa thức f(x).
Tìm a và b của đa thức g(x) biết rằng g(x) = 0 tại x = 1 và x = 4.
Chứng minh: g(x) = (1 – x)(x – 4).
Viết đa thức h(x) = f(x) + g(x) thành một tích.
Tìm nghiệm của h(x). (Tìm đủ các nghiệm)

Bài 8: Chứng minh rằng đa thức sau không có nghiệm trên tập hợp R:
a) f(x) = – 2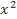 – 3.

b) g(y) = –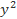 – 4y – 4.

c) h(x) = |x + 3| + |5 – x| + 7.

Bài 9: Cho hai đa thức f(x) = 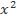+ 2mx + 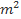và g(x) = 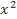+ (2m + 1)x + 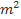. Hãy tìm m biết rằng f(1) = g(–1).

Bài 10: Tính tổng các hệ số của các hạng tử của đa thức nhận được sau khi đã khai triển và viết đa thức dưới dạng thu gọn:
f(x) = (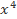 + 4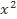 – 5x + 1)2004.(2 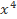– 4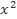 + 4x – 1)2005.
g(x) = (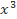 + 7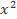 – 6x +5)2005.(3 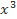– 9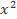 + 9x – 3)2006.