Chuyên Đề Hàm Số
I.Lý thuyết:
1. Khái niệm
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và gọi x là biến số.
2. Chú ý
- Hàm số có thể được cho bằng bảng, bằng lừoi, bằng công thức.... Khi hàm số được cho bằng công thức thì ta hiểu rằng biến số x chỉ nhận những giá trị làm cho công thức có nghĩa.
- Hàm số thường được kí hiệu y = f(x)
II. Bài tập vận dụng:
Bài 1: Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?
Hướng dẫn:
Vì mỗi giá trị của x ta xác định được chỉ một giá trị của y tương ứng nên đại lượng y là hàm số của đại lượng x.
Bài 2: Cho hàm số y = f(x) = 3x2 + 1. Tính f( ), f(1), f(3).
), f(1), f(3).
Hướng dẫn:
Ta có y = f(x) = 3x2 + 1. Do đó:
f( ) = 3.
) = 3. 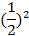 + 1 = 3.
+ 1 = 3.  + 1 =
+ 1 =  + 1 =
+ 1 =  .
.
Bài 3: Cho hàm số y= 5x - 1. Lập bảng giá trị tương ứng của y khi:
x = -5, -4, -3, -2, 0,  .
.
Hướng dẫn:
Cho hàm số y= 5x - 1. Lập bảng giá trị tương ứng của y khi:
Khi x = - thì y = 5.
thì y = 5. – 1 = 1 -1 = 0.
– 1 = 1 -1 = 0.
Ta lập bảng giá trị sau:
.png)
Bài 4: Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
.png)
Hướng dẫn:
a) Vì mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.
b) Đại lượng y là hàm số của đại lượng x.
Nhận xét: Với mọi x thì y luôn nhận một giá trị là 2 nên đây là một hàm hằng.
Bài 5: Cho hàm số y = f(x) = 12x.
a) f(5) = ? ; f(-3) = ?
b) Hãy điền các giá trị tương ứng của hàm số vào bảng sau:
.png)
Hướng dẫn:
a) f(5) = 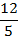 = 2,4; f(-3) =
= 2,4; f(-3) = 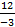 = -4.
= -4.
b) Lần lượt thay x bởi -6, -4 ; -3 ; 2 ; 5 ; 6 ; 12 vào công thức
y = f(x) = 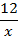
ta được các giá trị tương ứng y là -2, -3, -4, 6, 2, 4, 2, 1.
Ta được bảng sau:

Bài 6: Cho hàm số y = f(x) = x2 - 2. Hãy tính f(2) ; f(1) ; f(0) ; f(-1) ; f(-2).
Hướng dẫn giải:
Ta có y= f(x) = x2 - 2
Do đó f(2) = 22 - 2 = 4 - 2 = 2
f(1) = 12 - 2 = 1 - 2 = -1
f(0) = 02 - 2 = 0 - 2 = -2
f(-1) = (-1)2 - 2 = 1 - 2 = -1
f(-2) = (-2)2 - 2 = 4 - 2 = 2
III. Bài tập tự luyện:
Bài 1: Cho hàm số y = f(x) = |3x|.
Tìm x biết f(x) = 0; f(x) = 1; f(x) =  ; f(x) = 2010.
; f(x) = 2010.
Bài 2: Cho hàm số y = f(x) = |3x -1|.
Tìm x biết f(x) = 0; f(x) = 1; f(x) = 12; f(x) = 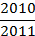 .
.
Bài 3: Cho hàm số y = f(x) = ax – 3.
Tìm a biết f(3) = 9, f(-3) = 6, f(-5) = 11.
Bài 4: Cho hàm số y = f(x) = (a + 2)x – 3a + 2.
Tìm a biết f(3) = 9, f(5) = 11, f(-1) =6.
Bài 5: Cho hàm số y = f(x) = ax +b.
Tìm a và b biết f(0) = -1, f(-2) = 3.
Bài 6: Cho hàm số y = f(x) = -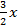 .
.
Tính f(1), f(-1), f(2), f(-2), f( ), f(-
), f(- ) và so sánh f(a) và f(-a).
) và so sánh f(a) và f(-a).
Bài 7: Cho hàm số y = f(x) = 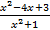
Tính f(0), f(1), f(-1), f(3), f(-3), f(4), f(-4).
Bài 8: Cho hàm số y = f(x) = 3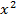 -2.
-2.
Tính f(1), f(-1), f(2), f(-2), f( ), f(-
), f(- ) và so sánh f(a) và f(-a).
) và so sánh f(a) và f(-a).
Bài 9: Cho hàm số y = f(x) = 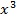 + x.
+ x.
Tính f(1), f(-1), f(2), f(-2), f( ), f(-
), f(- ) và so sánh f(a) và f(-a).
) và so sánh f(a) và f(-a).
Bài 10: Cho hàm số y = f(x) = 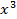 - 4x.
- 4x.
Tính f(1), f(-1), f(3), f(-3), f( ), f(-
), f(- ) và so sánh f(a) và f(-a).
) và so sánh f(a) và f(-a).
Bài 11: Cho hàm số y = f(x) = 5x.
Tìm x biết f(x) = 0; f(x) = 1, f(x) = -5, f(x) = 2010.
Bài 12: Cho hàm số y = f(x) = 5x -3.
Tìm x biết f(x) = 0; f(x) = 1, f(x) = -2011, f(x) = 2011.
Chúc các bạn học tốt.







